  Textbook Solutions Expert Q&A Practice Study Pack 

Chapter 6.1, Problem 9E 10 Bookmarks Show all steps: Find solutions for your homework Search
home / study / math / advanced mathematics / advanced mathematics solutions manuals / numerical analysis / 10th edition / chapter 6.1 / problem 9e

Numerical Analysis (10th Edition) Post a question

Answers from our experts for your tough
homework questions
See this solution in the app
Enter question

Problem Continue to post

19 questions remaining

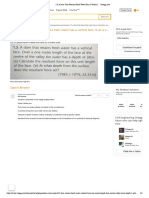
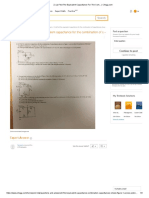
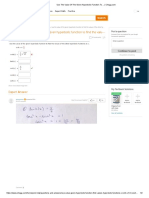
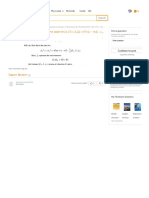
Given the linear system

Snap a photo from your

phone to post a question
a. Find value(s) of α for which the system has no solutions. We'll send you a one-time
download link
b. Find value(s) of α for which the system has an infinite number of solutions.

c. Assuming a unique solution exists for a given α, find the solution.

888-888-8888 Text me

By providing your phone number, you agree to receive

a one-time automated text message with a link to get
Step-by-step solution the app. Standard messaging rates may apply.

Step 1 of 7
My Textbook Solutions
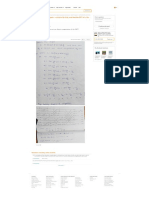
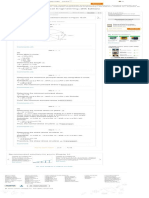
Consider the linear system,

…… (i)

Numerical Statistical Introduction

Write system (i) in matrix notation: Analysis Techniques... to Chemical...
10th Edition 14th Edition 7th Edition

View all solutions

Comment

Step 2 of 7

A system has,

(*) unique solution if

(**) infinitely many solutions if

(***) no solution if

Comment

Step 3 of 7

Augmented matrix associated with the above system is,

Observe that,

implies that

implies that

Comments (2)

How can we imply that -2 _18alpha^2 = 0 when the system says it is equal to 3-9alpha?
Where does that intuition come from?

The objective of the problem is to find where the system has and hasn't a solution. This
means where the bottom row becomes zero. So, you equal both equations to zero and
notice that they become zero when alpha is 1/3, but it has no solution when alpha is
-1/3 since the bottom row becomes 0=6, which is not possible.

Submit

Step 4 of 7

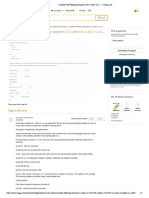
(a)

The objective is to find the value(s) of such that the system (i) has no solution.

For , the augmented matrix becomes,

Observe that

Note that

Hence the system (i) has no solution for .

Comments (1)

Shouldn't it be 2 and not -2 when you finish simplifying?

Submit

Step 5 of 7

(b)

The objective is to find the value(s) of such that the system (i) has infinite number of
solutions.

For , the augmented matrix becomes,

Note that

Hence the system (i) has infinite number of solutions for .

Comment

Step 6 of 7

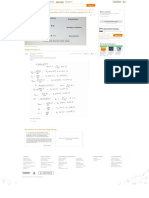
(c)

By assuming a unique solution exists for a given , find the solution.

From subpart (a), the system has no solution for , from subpart (b), system has infinite

number of solutions for . So, to get unique solution,

Suppose that .

For , the augmented matrix becomes,

…… (ii)

Observe that

Note that , hence the system (i) has unique solution for .

Comment

Step 7 of 7

To obtain that unique solution, write the reduced augmented matrix (ii) in equation notation as
shown:

From the equation get,

From the equation get,

Hence the unique solution is,

Comments (1)

why do all this work...choose a=0 u automatically get a matrix in REF

Submit

Was this solution helpful? 7 0

   Textbook Solutions Expert Q&A Practice Study Pack 

Chapter 6.1, Problem 9E 10 Bookmarks Show all steps: ON

   Textbook Solutions Expert Q&A Practice Study Pack 

Given the linear system Show that the operations a. ( λ E i ) → (Ei) b. (Ei +
a. Find value(s) of α for λEj) → (Ei) c. (Ei) ↔ (Ej) do not change the...
Chapter 6.1, Problem 9E 10 Bookmarks Show all steps: ON
which the system has no
solutions. b. Find value(s) See solution
of α...

See solution

See more problems in subjects you study

COMPANY LEGAL & POLICIES CHEGG PRODUCTS AND SERVICES CHEGG NETWORK CUSTOMER SERVICE
About Chegg Advertising Choices Cheap Textbooks Mobile Apps EasyBib Customer Service
Chegg For Good Cookie Notice Chegg Coupon Sell Textbooks Internships.com Give Us Feedback
College Marketing General Policies Chegg Play Solutions Manual Thinkful Help with eTextbooks
Corporate Development Intellectual Property Rights Chegg Study Help Study 101 Help to use EasyBib Plus
Investor Relations Terms of Use College Textbooks Textbook Rental Manage Chegg Study
Jobs Global Privacy Policy eTextbooks Used Textbooks Subscription
Join Our Affiliate Program DO NOT SELL MY INFO Flashcards Digital Access Codes Return Your Books
Media Center Honor Code Learn Chegg Money Textbook Return Policy
Site Map Honor Shield Chegg Math Solver

© 2003-2021 Chegg Inc. All rights reserved.