1 Problems section 7.

1
1.1 (F) → (?)
Evaluate the integral.
R R R
(a) (x2 + 2x) cos xdx (b) s2s ds (c) ln(x + 1)dx
R1 R9 ln y
(x2 + 1)e−x dx
R
(d) e2θ sin 3θdθ (e) 0
(f ) 4
√ dy
y

R2 (ln x)2 R R 2π
(g) 1 x3
dx (h) (arcsin x)2 dx (i) 0
t2 sin 2tdt

R √3 Rt
(j) 1
arctan( x1 )dx (k) 0
es sin(t − s)ds

1.2 (F)
R1
Suppose that f is continuous, f (0) = 0, f (1) = 1, f 0 (x) > 0, and 0
f (x)dx = 32 . Find
R1
the value of 0 f −1 (y)dy.

1.3 (F)
√
Find the area under the curve y = sin x from x = 0 to x = π 2 .

1.4 (F)
Prove that, for even powers of sine,

R π/2 1·3·5·····(2n−1) π
0
sin2n xdx = 2·4·6·····2n 2

1.5
Use integration by parts to prove the reduction formula.

R R
(ln x)n dx = x(ln x)n − n (ln x)n−1 dx

1.6 (F)
(a) Use integration by parts to show that

xf 0 (x)dx
R R
f (x)dx = xf (x) −

(b) If and are inverse functions and is continuous, prove that

Rb R f (b)
a
f (x)dx = bf (b) − af (a) − f (a)
g(y)dy

(c) In the case where f and g are positive functions and b > a > 0, draw a diagram
to give a geometric interpretation of part (b).
Re
(d) Use part (b) to evaluate 1 ln xdx

Calculus (I) — 2019.11.28 Section 7.1 1

2 Problems Plus
Rπ
Let In = 0
2
sinn xdx.
1. Show that I2n+2 ≤ I2n+1 ≤ I2n .

2. Use the following equation, for even powers of sine

π
1 · 3 · 5 · . . . · (2n − 1) π
Z
2
sin2n xdx =
0 2 · 4 · 6 · . . . · 2n 2
to show that
I2n+2 2n + 1
=
I2n 2n + 2
3. Use parts (1) and (2) to show that
2n + 1 I2n+1
≤ ≤1
2n + 2 I2n
I2n+1
and deduce that lim = 1.
n→∞ I2n

4. Use part (3) and the following equation, for odd powers of sine
π
2 · 4 · 6 · . . . · 2n
Z
2
sin2n+1 xdx =
0 3 · 5 · . . . · (2n + 1)

and for even powers of sine in part (2) to show that

2 2 4 4 6 6 2n 2n π
lim · · · · · · ... · · =
n→∞ 1 3 3 5 5 7 2n − 1 2n + 1 2
This formula is usually written as an infinite product:
π 2 2 4 4 6 6
= · · · · · · ...
2 1 3 3 5 5 7

and is called the Wallis product.

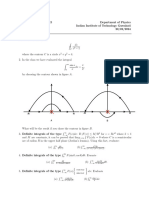
5. We construct rectangles as follows. Start with a square of area 1 and attach

rectangles of area 1 alternately beside or on top of the previous rectangle (see
the figure). Find the limit of the ratios of width to height of these rectangles.

Calculus (I) — 2019.11.28 Section 7.1 2