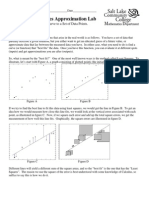
3.

2 Linear Functions
The basic fundamental function, the one that calculus is based upon, is the linear
function. A linear function is a function whose graph consists of segments of one
straight line throughout its domain.

Such a line is, you may remember, determined by any two points on it, say (a,
f(a)), (b, f(b))(a,f(a)),(b,f(b)). Thus, you can pick any aa and any bb in its
domain and determine the line from the two values, f(a)f(a) and f(b)f(b).

What is a formula for such a function?

We can determine the linear function which takes

value f(a)f(a) at aa and f(b)f(b) at bb by the following formula:

f(x) = f(a)\frac{x-b}{a-b} + f(b)\frac{x-a}{b-a}f(x)=f(a)a−bx−b

+f(b)b−ax−a

The first term is 00 when xx is bb and is f(a)f(a) when xx is aa, while the second

term is 00 when xx is aa and is f(b)f(b) when xx is bb. The sum of the two is
therefore f(a)f(a) when xx is aa and f(b)f(b) when xx is bb. And it is a linear
function. Linear functions have a term that is xx multiplied by some constant,
and may also have a constant term as well.

A more convenient and suggestive form for this function can be gotten by putting
the x terms together:

f(x) = mx + c = \frac{f(b) - f(a)}{b-a}x + \frac{f(a)b - f(b)a}{b-

a}f(x)=mx+c=b−af(b)−f(a)x+b−af(a)b−f(b)a

The number mm which occurs here is called the slope of this line. Notice

that mm is given by the ratio of the change of ff between x = bx=b and x =
ax=a to the change in xx between these two arguments:

m = \frac{f(b) - f(a)}{b-a}m=b−af(b)−f(a)

If ff is plotted, where f(x)f(x) meets the yy axis is what we call cc here. It is called

the y-intercept of this line, which is the value of yy when xx is 00.
There is a mathlet here which allows you to vary the slope mm and y-intercept c
and see what that does to a line. You should fiddle with this mathlet and from it get
an idea what the slope mm tells you about the line. Using it you can construct your
own examples.

You can actually construct a spreadsheet that can do the same thing as this applet.
You would be wise to do so. Directions on exactly how can be reached by clicking
here.

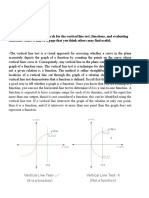
I know all this stuff. Why do you waste my time with it ?

All this may sound simple to you, but if you understand it, you are well on your
way to understanding calculus. Realize that calculus consists of studying functions
through studying the slopes of the straight lines they resemble near any given
argument. Here are some exercises to help you get used to these things.

Exercises:

3.3 Play with the applet until you get a feel for the geometric meaning of the
slope of a line. Then take a piece of paper, draw x and y axes on it and put
scales on them, and have a friend draw some straight lines on the paper.
Without measuring, guess the slopes of the lines. Now measure the lines
(change in y over change in xx) and see how good your guesses were.

3.4 When is the slope of a line negative? When is it 00? When is it 11? When -
1−1? If you use the same scale for xx and yy, what does slope 10 look like?
How about slope -\frac{1}{10}−101?

3.5 Follow the directions that you can get to above to construct a spreadsheet
that can work as the applet here. Try it with the various slopes of the last
question.

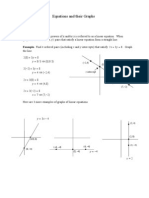
3.6 Construct the linear function, gg, with slope 2 satisfying g(1) = 1g(1)=1;

graph it. What is g(4)g(4)? Do the same for the linear function, hh, which
satisfies h(1) = 4h(1)=4, h(4) = 12h(4)=12. What is the slope of hh?