2019 JC1 H2 Mathematics (9758)

Term 2 Revision Test

Date: 4 June 2019 45 minutes

Name : CG :
Marks: 25
Answer all 3 questions.

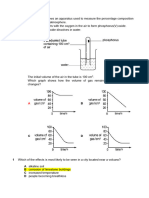
1 Without using a calculator, solve the inequality

x 4
 . [4]
x 1 x  2
x2 4
Hence solve the inequality  2 . [2]
x 1 x  2
2


 
 

2 Referred to the origin O, the points A, B and D are such that OA  a , OB  b and OD  d.
π
The point C is such that OACB is a parallelogram and angle AOB is radians.
3

 

(i) Given that a is a unit vector and b  4 , find the length of projection of OC onto OA .
[3]
(ii) Given that  a   b  d = 0 and     1  0 , show that A, B and D are collinear. [3]
If   4 , find the exact area of triangle OBD. [3]

  
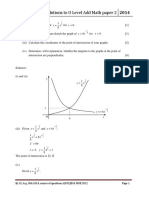
3 The function f is defined by f ( x)  2sin  x   , x  ,   x  .
 6 6
(i) Sketch the graph of y  f ( x) , giving the exact coordinates of the turning point and the
end-points. Deduce the exact range of f . [4]


The domain of f is further restricted to p  x  . State the smallest value of p for which
6
the function f 1 exists. [1]

Using this restricted domain for the rest of the question,

(ii) find f 1 ( x ) and state the domain of f 1 . [2]
The function g is defined by

 1
 2  x  1 , x  ,  1  x  0,
g( x)  
 1  x  2 3 , x  , 0  x  2.
 16
(iii) Sketch the graph of y  g( x) . [2]
(iv) Explain why the composite function fg exists. [1]