Bessel Differential Equation

The linear second order ordinary differential equation of type x2 y ″

+ xy ' +( x 2−v 2 ) y = 0
Is called the Bessel equation. The number v is called thee order of the
Bessel equation.
The given differential equation is named after the German
mathematician astronomer Friedrich Wilhelm Bessel who studied this
equation in detail and showed (in 1824) that its solutions are expressed
in terms of a special class of functions called cylinder functions or
Bessel functions.
Concrete representation of the general solution depends on the number v.
Further we consider separately two cases:
 The order v is non-integer;
 The order v is an integer.
Case 1. The Order v is Non-Integer
Assuming that the number v is non-integer and positive, the general
solution of the Bessel equation can be written as
y ( x ) =C1 J v ( x ) + C2 J −v ( x ),
where C1, C2 are arbitrary constants and J v ( x ) , J − v ( x ) are Bessel functions of
the first kind.
The Bessel function can be represented by a series, the terms of which
are expressed using the so-called Gamma function:
∞
(−1 ) p x 2 p +v
Jv ( x ) =∑
p=0 Ґ ( p+ 1 ) Ґ ( p+v +1 ) 2()
The Gamma function is the generalization of the factorial function from
integers to all real numbers. It has, in particular, the following
properties:
Ґ ( p +1 )= p ! , Ґ ( p+ v +1 )=( v+ 1 )( v+ 2 ) … … ( v+ p ) Ґ ( v +1 ) .

The Bessel functions of the negative order ¿) (assuming that v > 0) are
written in similar way:
∞
(−1 ) p x 2 p −v
J −v ( x ) =∑
p=0 Ґ ( p+ 1 ) Ґ ( p+v +1 )()
2

The Bessel functions can be calculated in most mathematical software

packages as well as in MS Excel. For example, the Bessel functions of
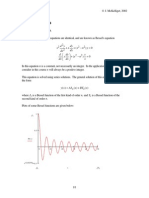
the 1st kind of orders v=0 to v=4 are shown in Figure 1.

Figure 1

Case 2. The Order v is an integer

If the order v of the Bessel differetial euation is an integer, the Bessel
functions J v ( x )∧J − v ( x ) can become dependent from each other. In this cae
the general solution is decribed by another formula:
y ( x ) =C1 J v ( x ) + C2 Y v ( x ),
Where Y v ( x ) is the Bessel function of the second kind. Sometimes this
family of functions is also called Neumann functions or Weber
functions.
The Bessel function of the second kind Y v ( x ) can be expressed in terms of
the Bessel functions of the first kind J v ( x ) and J −v ( x) :
J v (x)cos πv−J − v (x )
Y v ( x )=
sin πv

The graph of the functions Y v ( x ) for several first orders v are shown in
Figure 2.

Figure 2

Note:
Actually the general solution of the differential equation expressed in
terms of Bessel functions of the functions of the first and second kind is
valid for non-integer orders as well.