SPH4U 7.3-7.

4 Electric Field and Potential Difference

Electric Field (𝜀⃗):_____________________________________________________________________________________

__________________________________________________________________________________________________

__________________________________________________________________________________________________

 Any isolated point charge produces an electric field, which is a region in which a
force is exerted on an electric charge.

 Were another charge to enter this field, the electric field would exert a force on it.

 The electric field has both _________________________________, so electric field

is a vector denoted by 𝜀⃗.

Force in a Field

 Consider a particular point in space where there is a uniform (unchanging) electric field, 𝜀⃗

 A point charge or an arrangement of several charges may have produced this

field.

 A charge q at this location in the field

____________________________________ and experience an electric force
given by

 Where the electric force, 𝐹⃗𝐸 , is thus ____________________________, with

direction depending on whether the charge is positive or negative.

Test Charge

 The charge q1 is called a ____________________.

 By measuring the force on a positive test charge, q1, you can determine ________________________________

___________________________________________________________________________________________

 Since we are working with a positive test charge, q1, the electric field ___________________________________
that the test charge experiences.

Homework 7.3 p345 Q 2, 3, 4, 5, 6 7.4 p354 Q 1, 2, 3, 4, 5, 7

 SPH4U 7.3-7.4 Electric Field and Potential Difference

Electric Field and Electric Force

 Coulomb’s law for electric force allows you to calculate the electric field using the amount of charge that
produces the field, q2, and the distance of the field from the charge.

 Inserting this expression into the equation relating electric force to the electric field gives the result.

 In this equation q = q1, so we get

 This is the magnitude of the electric field ____________________________________________________.

 The direction of 𝜀⃗ lies ____________________________________________________________________

______________________________________________________________________________________

Example

Calculate the magnitude and direction of the electric field at a point 2.50 m to the right of a positive point charge

q = 6.25 x 10-6 C.

Homework 7.3 p345 Q 2, 3, 4, 5, 6 7.4 p354 Q 1, 2, 3, 4, 5, 7

 SPH4U 7.3-7.4 Electric Field and Potential Difference

Your Turn

An electric force with a magnitude of 2.5 N, directed to the left, acts on a negative charge of 25.0 C.

(a) Determine the electric field in which the charge is located.

(b) Calculate the electric field when the force is the same but the charge is -0.75 C.

Calculate the electric field at point Z in Figure 5, due to the point charges
q1 = 5.56 x 10-9 C at point X and q2 = -1.23 x 10-9 C at point Y.

Homework 7.3 p345 Q 2, 3, 4, 5, 6 7.4 p354 Q 1, 2, 3, 4, 5, 7

 SPH4U 7.3-7.4 Electric Field and Potential Difference

Electric Field Lines:___________________________________________________________________________________

__________________________________________________________________________________________________

__________________________________________________________________________________________________

The electric field lines are parallel to 𝜀⃗, and the density of the field lines is proportional to the magnitude of 𝜀⃗.

Three-Dimensional Field Analysis

Electric Dipoles:_____________________________________________________________________________________

__________________________________________________________________________________________________

The two charges in an electric dipole give rise to a more complicated electric field than the one associated with a single
electric charge.

Homework 7.3 p345 Q 2, 3, 4, 5, 6 7.4 p354 Q 1, 2, 3, 4, 5, 7

 SPH4U 7.3-7.4 Electric Field and Potential Difference

Electric Dipole – Vector Sum : Field Interactions

Homework 7.3 p345 Q 2, 3, 4, 5, 6 7.4 p354 Q 1, 2, 3, 4, 5, 7

 SPH4U 7.3-7.4 Electric Field and Potential Difference

Plate Charges

 Instead of point charges, suppose you have two parallel planes of charge.

 As with the dipole, one plane has a positive charge and the other plane has a negative charge.

 In both cases, ________________________________________________________________

 These field lines are __________________________________________________________________________.

 At any location between the planes, _____________________________________________________________.

 Outside the planes, the __________________________________ from all the individual charges in the two
parallel planes yields a _______________________________.

Work and Electric Potential Difference

 A ______________________ in the ______________________ experiences an

_____________________

 Suppose this charge ___________________________________starting at

point A and ending at point B. For simplicity, assume _________________

_________________________________________________.

 According to the __________________________________________ the

electric force on the charge is

Homework 7.3 p345 Q 2, 3, 4, 5, 6 7.4 p354 Q 1, 2, 3, 4, 5, 7

 SPH4U 7.3-7.4 Electric Field and Potential Difference

Electric Potential Energy (EE):__________________________________________________________________________

__________________________________________________________________________________________________

__________________________________________________________________________________________________

 We can now define the electric potential energy, EE, which is the energy stored in the system that can do work
W on a positively charged particle.

 So, if the electric force does an amount of work W on a charged particle, the change in the electric potential
energy is

 Combining this equation with the equation relating force to the electric field, the change in electric potential
energy when the charged particle moves from A to B

 Electric potential energy is stored _______________________________________________________________.

 the charge q is _______________________________________________________________________________.

Homework 7.3 p345 Q 2, 3, 4, 5, 6 7.4 p354 Q 1, 2, 3, 4, 5, 7

 SPH4U 7.3-7.4 Electric Field and Potential Difference

Example

An electron experiences a change in kinetic energy of +4.2 x 10-16 J. Calculate the magnitude and direction of the electric
field when the electron travels 0.18 m toward the right.

Your Turn

Calculate the work done in moving a proton 0.75 m in the same direction as the electric field with a strength of 23 N/C.

Electric Potential (V):________________________________________________________________________________

__________________________________________________________________________________________________

__________________________________________________________________________________________________

 Electric potential, V, is a measure of how much electric potential energy is associated with a specific quantity of
charge at a particular location in an electric field.

 The SI unit of electric potential is the volt (V), named in honour of physicist Alessandro Volta (1745–1827). The
volt relates to other SI units in the following equation:

Homework 7.3 p345 Q 2, 3, 4, 5, 6 7.4 p354 Q 1, 2, 3, 4, 5, 7

 SPH4U 7.3-7.4 Electric Field and Potential Difference

Electric Potential Difference (ΔV):_______________________________________________________________________

__________________________________________________________________________________________________

__________________________________________________________________________________________________

 You can define the change in the potential, or potential difference, for a charge q that moves between two
points

 For the case of a uniform electric field, the equation for electric potential difference becomes

 This relationship shows how a non-uniform electric field varies with the change in electric potential (that is,
electric potential difference) and the change in position in the field:

 Positive point charges will naturally travel from _____________________________________________________

___________________________________________________________________________________________

 Electrons will naturally travel from _______________________________________________________________

___________________________________________________________________________________________

Homework 7.3 p345 Q 2, 3, 4, 5, 6 7.4 p354 Q 1, 2, 3, 4, 5, 7

 SPH4U 7.3-7.4 Electric Field and Potential Difference

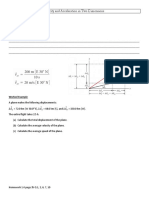
Example

Four parallel plates are connected in a vacuum as shown in Figure 6. An electron at

rest in the hole of plate X is accelerated to the right. The electron passes through
holes at W and Y with no acceleration at all. It then passes through the hole at Y and
slows down as it heads to plate Z.

(a) Calculate the speed of the electron at hole W.

(b) Calculate the distance, in centimetres, from plate Z to the point at which the
electron changes direction.

Your Turn

An old television cathode-ray tube creates a potential difference of 1.6 x 104 V across the parallel accelerating plates.
These plates accelerate a beam of electrons toward the target phosphor screen. The separation between the plates is 12
cm.

(a) Using the principle of energy conservation and the definition of electric potential difference, calculate the speed
at which the electrons strike the screen.

(b) Calculate the magnitude of the electric field.

Homework 7.3 p345 Q 2, 3, 4, 5, 6 7.4 p354 Q 1, 2, 3, 4, 5, 7

 SPH4U 7.3-7.4 Electric Field and Potential Difference

Your Turn

An electron enters a parallel plate apparatus that is 8.0 cm long and 4.0
cm wide, as shown in Figure 7. The electron has a horizontal speed of 6.0
x 107 m/s. The potential difference between the plates is 6.0 x 102 V.
Calculate the electron’s velocity as it leaves the plates.

Homework 7.3 p345 Q 2, 3, 4, 5, 6 7.4 p354 Q 1, 2, 3, 4, 5, 7