STUDENT NAME: GRADE/SECTION:

TEACHER: DATE SUBMITTED:

PRE-CALCULUS- Grade 11-Week 11

Illustrating Inverse Trigonometric Functions

You’ve studied about the six trigonometric functions, and you know about inverse
functions, so it's time to learn about inverse trigonometric functions. Recall that when trying
to find the inverse of a function like f ( x )= √ x , you change this into y= √ x and then make
x∧ y swap places. Then solve for y .
y= √ x
x=√ y
2
y=x
−1 2
f (x)=x
Essentially inverse functions sequentially undo anything operating on x in the original
function.

inverse must undo f −1 (x)=x2

f ( x )= √ x
operations

Now try y=sin x .

y=sin x Interchange x & y , then solve for y .

x=sin y
−1
s∈¿ x=s ∈¿ ¿ ¿ ¿
−1
The only way to solve for y is to take the inverse sine
−1
y=s∈¿ x ¿ of both sides. This will cancel out the sine operation on
y.

ROV_Pre-Calculus_Grade 11_Q2_Wk 7_LP11

 −1 1 1
Note that y=s∈¿ x≠ ¿ because =¿ ¿ which you already know is csc x .
sin x sin x

Sine Inverse Sine

y=sin x y=s∈¿ x ¿
−1

angle Corresponding
sine value
angle sine value

Inverse sine can also be represented this way: y=arcsin x .

You should note that for a function to have an inverse function, it must pass the
horizontal line test because when you find the inverse, you are reflecting the function across
the line y=x . The domain and range should follow the one-to-one rule to make it work as a
function. So to solve the inverse of the trigonometric functions, you should restrict the
−π π
domain. For y=sin x , you will look at a restricted domain from ¿ .
2 2
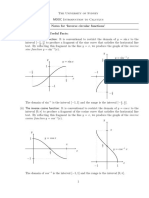
To sketch the graph of y=sin−1 x , let’s make a table of values for y=sin x and
y=sin−1 x . Recall that the graphs of y=sin x and y=sin−1 x are symmetric with respect to
the line y=x . This means that if a point (a , b) is on y=sin x , then ( b , a ) is on y=sin−1 x .
−π −π −π −π π π π π
x 0
2 3 4 6 6 4 3 2
y=sin x
−√ 3 −√ 2 −1 1 √2 √3
y −1 0 −1
2 2 2 2 2 2

−√ 3 −√ 2 −1 1 √2 √3
x −1 0 −1
−1 2 2 2 2 2 2
y=sin x
−π −π −π −π π π π π
y 0
2 3 4 6 6 4 3 2

y=sin x y=s∈¿−1 x ¿
Domain: [−1,1]

−π π
Range: [ , ]
2 2

ROV_Pre-Calculus_Grade 11_Q2_Wk 7_LP11

 Example 1: Find the exact value of each expression.

a) arcsin (
√2 )
2
b) arcsin (−1)
−1 −1
c) sin ( )
2

Solution:
a) If you recall the unit circle, the

angle that gives a sine value of

√2
2

is
π
4 ( )
. Hence arcsin
√2 = π
2 4
b) The angle that gives a sine value
−π
of −1is . Hence
2
π
arcsin (−1 )=−¿ ¿.
2
c) The angle that gives a sine value
−1 −π
of is . Hence
2 6
arcsin
−1
2 ( ) π
=¿− ¿.
6

Example 2: Sketch the graph and find the domain and range of y=sin−1 (x +1) .

Solution: Because y=sin−1 ( x +1) can be written as y=sin−1 [ x−(−1 ) ], then, the
graph of y=sin−1 ( x +1 ) shifted 1-unit to the left of y=sin−1 ( x) .

Domain: [−2,0]

−π π
Range: [ , ]
2 2

ROV_Pre-Calculus_Grade 11_Q2_Wk 7_LP11

Inverse of Cosine Function
The development of the other inverse trigonometric functions is similar to that of the
inverse sine function-they just differ in the restriction for the domain. For y=cos−1 x , the
domain is restricted from 0 to π .
Below are the table of values and graph of y=cos x and y=cos−1 x .
π π π π 2π π 3π
x 0 π
6 4 3 2 3 4 4
y=cos x
y 1
√3 √2 1
0
−1 −√ 2 −√ 3
-1
2 2 2 2 2 2

x 1
√3 √2 1
0
−1 −√ 2 −√ 3
-1
−1 2 2 2 2 2 2
y=cos x
π π π π 2π π 3π
y 0 π
6 4 3 2 3 4 4

y=cos x y=cos x
−1

Domain: [−1,1]

Range: [0 , π ]

Example 3: Sketch the graph and find the domain and range of y=cos−1 (2 x) .

ROV_Pre-Calculus_Grade 11_Q2_Wk 7_LP11

 Solution: In graphing y=cos−1 ( 2 x ) , the horizontal length of y=cos−1 (x ) is reduced in
half, while the vertical height remains the same. This comparison technique is shown below
with the graph of y=cos−1 (x ) in broken line and the graph of y=cos−1 (2 x) in solid line.

Domain: [ −1 1
,
2 2 ]
Range: [0 , π ]

Example 4: Find the exact value of each expression.

d) arccos(0)
−√ 3
e) arccos( )
2
−1 1
f) cos ( )
2

Solution:
d. If you recall the unit circle, the angle
that gives a cosine value of 0 is half π .
π
Hence arcsin ( 0 )=
2
e. The angle that gives a cosine value
−√ 3 5π
of is . Hence
2 6

( )
arcsin √ = .
− 3 5π
2 6
1
The angle that gives a cosine value of
2

is
π
3
. Hence arccos ()
1
2
π
=¿ ¿ .
3

Inverse of Tangent Function

The inverse of tangent function is similarly defined as inverse sine and cosine functions. The
domain of y=tan −1 x or y=arctan x is R .

ROV_Pre-Calculus_Grade 11_Q2_Wk 7_LP11

 y=tan −1 x or y=arctan x
means
tan y =x
−π π
where xϵ R and ≤ y≤ .
2 2

y=tan x y=arctan x

The value of arccos x , arcsin x , and other trigonometric function are called principal
values since these are selected from a restricted domain. The table below shows the domain
and principal values of the remaining inverse trigonometric functions. These are most
convenient range used in various fields in Mathematics, particularly in Calculus.
Function Graph Domain and Range

−1
Domain: (−∞ ,−1 ] ∪ ¿
y=sec x
Range: 0 , [ )π
2
∪¿

−1
Domain: (−∞ ,−1 ] ∪ ¿
y=csc x
Range: [ −π
2 )
,0 ∪ ¿

y=cot−1 x Domain: {x ∈ R }
Range: (0 , π)

ROV_Pre-Calculus_Grade 11_Q2_Wk 7_LP11

 Example 5: Sketch the graph and find the domain and range of

a. f (x)=sec −1 ( x +2)
b. f ( x )=csc−1 (x−3)
Solution:
a. In graphing f (x)=sec −1 ( x+ 2 ), the graph of f ( x)=sec −1 ( x )shifted 2 units to the
left, while the vertical height remains the same.

Domain: (−∞ ,−3 ] ∪ ¿

[ )
Range: 0 ,
π
2
∪¿

b. In graphing f ( x )=csc−1 ( x−3 )the graph of f ( x )=csc−1 ( x)shifted 3 units to the left,
while the vertical height remains the same.

ROV_Pre-Calculus_Grade 11_Q2_Wk 7_LP11

 Domain: (−∞ , 2 ] ∪ ¿

Range: [ −π
2 )
,0 ∪ ¿

Learning Competency with code

Illustrate the domain and range of inverse trigonometric functions

(STEM_PC11T-IIh-1)

Activities

Activity 1: Choose the letter of the correct answer from the choices given. Write your
answer on a separate sheet of paper.
_______1. Which among the following is read as inverse of sine x?
a. sin x b. sinarc x c. sin −1 x d. sin−2 x
1
_______2. What is the value of x in sin x= ?
2
π π π π
a. b. c. d.
3 4 5 6
_______3. Which of the following inverse trigonometric functions has no restriction in the
domain?
a. y=sin−1 x b. y=cos−1 x c. y=tan −1 x d. y=csc−1 x

_______4. What is the exact value of sec

−1
( −23√3 ) ?
2π −2 π −5 π
a. b. c. d. π
3 3 6
_______5. What is the range of y=cos−1 3 x?

a. [
−1 1
3 3
,
] b. [−3,3] c. . (
−1 1
, )
3 3
d. (−3,3 ¿

ROV_Pre-Calculus_Grade 11_Q2_Wk 7_LP11

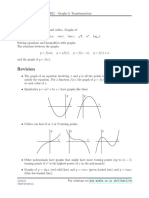
 Activity 2: Sketch the graph of the following inverse trigonometric functions.
x−1
1. y=sin
3
2. y=cos−1 ( x−2)
3. y=tan −1 2 x

Rubric for Activity 2:

POINTS CRITERIA
Performed complete and correct procedure and the graph is
5
sketched accurately.
Performed complete and correct procedure but made
4
minimal error with the graph.
Performed complete procedure but with errors leading to
3
inaccurate sketch of the graph.
Performed the procedure incompletely leading to incomplete
2
and inaccurate sketch of the graph.
Performed a wrong and incomplete procedure leading to
1
incorrect sketch of the graph.
0 No answer and calculation performed.

How did you find the activities? Draw an emoticon that would describe it
and why?

ROV_Pre-Calculus_Grade 11_Q2_Wk 7_LP11

Bacani, Jerico B.PhD, et. Al., Teaching Guide for Senior High School: Precalculus (Quezon
City: Commission on Higher Education, 2016), pp. 125 - 180.
Real Life Applications of Trigonometry | Mathnasium. Mathnasium® | Face-to-Face &
Online Math Tutoring. Last modified October 16, 2017.
https://www.mathnasium.com/real-life-applications-of-trigonometry.
Trigonometry for Solving Problems | Trigonometry, Math School, High School Math
Activities. Pinterest. Accessed October 23, 2021.

Activity 1. 1)C 2)D 3)C 4)B 5)A

Activity 2
1.

2.

3.

Prepared by:

JOSE BENAVENTE
San Jose National High School

ROV_Pre-Calculus_Grade 11_Q2_Wk 7_LP11