Module 3 – Motion in 2 Dimensions and 3 Dimensions

Kinematics in Two and Three Dimensions

Module 3

EXPECTED LEARNING OUTCOMES

3.1 Deduce the consequences of the independence of vertical and horizontal components of
projectile motion
3.2 Calculate range, time of flight, and maximum heights of projectiles
3.3 Infer quantities associated with circular motion such as tangential velocity, centripetal
acceleration, tangential acceleration, radius of curvature
3.4 Solve problems involving two-dimensional motion in contexts such as, but not limited to
ledge jumping, movie stunts, basketball, safe locations during firework displays, and
Ferris wheels

THE BIG IDEA

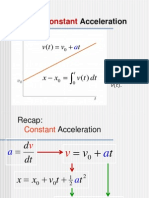
In the last chapter we developed the concepts of position, displacement, velocity, and
acceleration that are needed to describe the motion of an object along a straight line. We found that the
directional aspect of these quantities can be taken care of by + and – signs, as in one dimension only
two directions are possible. Now, we will deal with the kinematics of a particle moving in two
dimensions. Knowing the basics of two-dimensional motion will allow us to examine— in future
chapters—a wide variety of motions, ranging from the motion of satellites in orbit to the motion of
electrons in a uniform electric field. We begin by studying in greater detail the vector nature of
displacement, velocity, and acceleration. As in the case of one-dimensional motion, we derive the
kinematic equations for two-dimensional motion from the fundamental definitions of these three

[Grade 12 – Classical Physics I (Calculus Based)] 28

 Module 3 – Motion in 2 Dimensions and 3 Dimensions

quantities. We then treat projectile motion and uniform circular motion as special cases of motion in
two dimensions. We also discuss the concept of relative motion, which shows why observers in
different frames of reference may measure different displacements, velocities, and accelerations for a
given particle. Motion not confined to a plane, such as a car following a winding mountain road, is
described by three-dimensional kinematics and thus, the real world is three-dimensional. In this
module, we will examine and answer the question, why do we study motion in more than one
dimensions?

DEEPEN YOUR UNDERSTANDING

PROJECTILE MOTION
Projectile motion is the motion of an object thrown or
projected into the air, subject to only the acceleration of gravity. The
object is called a projectile, and its path is called its trajectory. The Did you know that?
motion of falling objects is a simple one-dimensional type of projectile
If a gun is fired
motion in which there is no horizontal movement. In this discussion, horizontally, and at the
we consider two-dimensional projectile motion, such as that of a same time a bullet is
football or other object for which air resistance is negligible. dropped from the same
The most important fact to remember here is that motions along height. They both hit the
perpendicular axes are independent and thus can be analyzed ground at the same time.
separately. The key to analyzing two-dimensional projectile motion is
to break it into two motions, one along the horizontal axis and the other along the vertical. Projectile
motion is a combination of uniform horizontal motion and free fall. These two components of projectile
motion are independent from each other. Just like in free fall, projectile motion also exhibits time and
speed symmetries along its vertical components.
For a projectile fired from the ground at an angle θ above the horizontal, the projectile rises to
some maximum height and then descends. It finally lands at some horizontal displacement from its
launching point. This horizontal displacement is called range. The magnitude of the range, usually
represented by R, is the horizontal distance traveled by the projectile between the launching position
and landing position, on the assumption that it returns to the same level at which it is fired.
When describing projectile motion, a coordinate system is used in which the positive y direction
is pointing upward, and the positive x direction is pointing to the right. The acceleration of gravity is in
the negative y direction.
vy = 0
vy = v0 sinθ
v0 vx = v0 cosθ

θ
vx = v0 cosθ

vx = v0 cosθ

vy = v0 sinθ
v

Range

The trajectory of a projectile thrown upward with initial velocity v0 at θ with the horizontal

[Grade 12 – Classical Physics I (Calculus Based)] 29

 Module 3 – Motion in 2 Dimensions and 3 Dimensions

As the figure above indicates, a projectile launched with an initial speed v0 at an angle θ will
have initial velocity components
vx0 = v0 cosθ and vy0 = v0 sinθ.
The launching speed and angle at which a projectile is launched affects the projectile’s
trajectory. The horizontal component of the projectile’s velocity is constant, and acceleration is 0 m/s2,
while the vertical component of velocity is changing, and acceleration is due to gravity.
The range is dependent on the angle of projection. It can be shown that maximum range occurs
when the angle of projection is 45o. It can also be shown that same ranges are obtained for two identical
projectiles fired at equal initial speeds if their angles of projection are complementary. For example,
projectiles launched at angles of projection of 30 o and 60o for a given initial velocity cover the same
range.

For the same initial speed, the same range is obtained for two projection angles that are complementary.

Example: A rifle is aimed horizontally at a target 30 m away. The bullet hits the target 1.9 cm below
the aiming point. (a) What is the bullet’s time of flight? (b) What is the muzzle velocity?

Solution: (a) First, we define our coordinates. We will use the coordinate system indicated in the
figure, where the origin is placed at the tip of the gun. Then we have x0 = 0 and y0 = 0.
We also know the acceleration:
ax = 0 and ay = −9.80 m/s2 = −g
The gun is fired horizontally so that v0y = 0, but we do not know v0x. We do not know the time
of flight, but we do know that when x has the value 30 m then y has the value −1.9 × 10−2 m
(1.9 cm).
Our equation for the y coordinate is (4th Kinematic Equation in y terms)
y = y0yt + ½ ayt2
y = 0 + ½ (–g)t2
y = –½ gt2
We can now ask: “At what time, t, does y equal −1.9 × 10−2 m?” Substitute y = −1.9 × 10−2 m
and solve:
y = –½ gt2
–2y
t2 =
g
–2(−1.9 × 10−2 m)
t2 =
9.80 m/s2
t = 0.00387755102 or 3.88 × 10−2 s2
2

[Grade 12 – Classical Physics I (Calculus Based)] 30

 Module 3 – Motion in 2 Dimensions and 3 Dimensions

Getting square root of both sides we obtain,

t = 0.0623 or 6.23 × 10−2 s
Since this is the time of impact with the target, the time of flight of the bullet is t = 6.23 ×
10−2 s.
(b) The equation for x−motion is
x = v0xt + ½ axt2
x = v0xt + ½ (0)t2
x = v0xt
From part (a) we know that when t = 6.23 × 10−2 s then x = 30 m. This allows us to solve for
v0x: x
v0x =
t
30 m
v0x =
6.23 × 10−2 s
v0x = 481.54 m/s
The muzzle velocity of the bullet is 481.54 m/s.

Example: You throw a ball with a speed of 25 m/s at an angle of 40o above the horizontal directly toward
a wall, as shown in the figure. The wall is 22 m from the release point of the ball. (a) How
long does the ball take to reach the wall? (b) How far above the release point does the ball hit
the wall? (c) What are the horizontal and vertical components of its velocity as it hits the wall?
Solution: (a) We will use a coordinate system which has its origin at the point of firing, which we take
to be at ground level.

It is when the x coordinate of the ball is equal to 22 m. Then let us write out the x−equation of
motion for the ball. The ball’s initial x− velocity is
v0x = v0 cos θ0 = (25.0 m/s) cos 40o = 19.2 m/s
and of course, ax = 0, so that the x motion is given by
x = v0xt + ½ axt2 = (19.2 m/s) t + ½ (0)t2
We solve for the time at which x = 22 m:
22 m = (19.2 m/s) t
22 m
t=
19.2 m/s
t = 1.15 s
The ball hits the wall 1.15 s after being thrown.
(b) We will be able to answer this question if we can find the y coordinate of the ball at the time
that it hits the wall, namely at t = 1.15 s.
We need the y equation of motion. The initial y velocity of the ball is
v0y = v0 sinθ0 = (25 m/s) sin 40o = 16.07 m/s
and the y acceleration of the ball is ay = −g giving:
y = v0yt + ½ ayt2 = (16.07 m/s) t – ½ gt2
which we use to find the y coordinate at t = 1.15 s:
y = (16.07 m/s) (1.15 s) – ½ (9.80 m/s2) (1.15 s)2
y = 12 m
which tells us that the ball hits the wall at 12 m above the ground level (above the release
point).

[Grade 12 – Classical Physics I (Calculus Based)] 31

 Module 3 – Motion in 2 Dimensions and 3 Dimensions

(c) The x and y components of the ball’s velocity at the time of impact, namely at t = 1.15 s are
found from 2nd Kinematic equation:
v – v0
a=
t
Manipulating the equation, we obtain
vx = v0x + axt = 19.2 m/s + (0)t = 19.2 m/s
and
vy = v0y + ayt = 16.07 m/s + (−9.80 m/s2) (1.15 s)
vy = +4.80 m/s.

CIRCULAR MOTION
Another type of two-dimensional motion worth studying about
is circular motion. A car rounding a rotunda, the recreational rides such
as Ferris wheels and carousels, satellites orbiting Earth, and a yo-yo Did you know that?
whirling on a string are examples of circular motion.
Uniform circular motion is the motion of an object traveling The best way to brush
at a constant speed on a circular path. If the speed varies, then it is called your teeth is in a circular
nonuniform circular motion. The number of cycles or revolutions a motion. Always brush
body has completed per unit of time is called frequency, f. On the other your teeth at a 45-degree
angle for the best results.
hand, the time for an object to have one complete revolution is called
period, T. Notice that assumed in this definition is the circular path
(with a given radius, r) that defines the trajectory of the motion. Also notice that the velocity, v, at any
time is along the tangent of the circular path at where the object is.

A racing car moving in uniform circular motion

The circumference of a circle over the amount of time the object travelled in either in terms of
frequency or period is referred to as tangential speed. The velocity v of a body moving in a circular path
with radius of curvature r at any instant is directed tangentially. Hence, it is called tangential velocity.
The direction of tangential velocity is always changing but its magnitude may or may not be constant.
To explain the concept of tangential velocity, suppose you are whirling a tennis ball on a string around
in circles, then suddenly the string suddenly snaps. What direction does the tennis ball fly?

3
2

Since instant velocity at any point is tangent to the circle, then the tennis ball will fly at number
3 direction.

[Grade 12 – Classical Physics I (Calculus Based)] 32

 Module 3 – Motion in 2 Dimensions and 3 Dimensions

The fact that the direction of motion of an object in a circular motion change continuously with
time suggests that the velocity vector of the object varies continuously with time. Hence the motion
must have an acceleration, a. Acceleration may be resolved into two components: (1) a component
tangent to the circular path and (2) a component directed towards the center of the circle. The first
component is called tangential acceleration, represented by at, which may be parallel or antiparallel to
tangential velocity, v. The second component is what we call accelerations giving rise to circular
motions and perpendicular to the circular path and that is called centripetal accelerations, denoted by
ar. This account changes in the direction of the velocity.
The acceleration of the particle is directed toward the center of the circle and has magnitude
v2
ar = r
where r is the radius of the circular path and v is the (constant) speed of the particle. Because of the
direction of the acceleration (i.e., toward the center), we say that a particle in uniform circular motion
has a centripetal acceleration.

Example: A child sits at a distance of 3 m from the axis of merry-go-around in an amusement park. If
merry-go-around makes 2 revolutions in 5 s, find (a) the tangential speed and (b) centripetal
acceleration of the child.
Solution: (a) Let the radius of curvature be r = 3 m. The distance that the child travels if the merry-go-
round makes 2 revolutions in two times the circumference of her circumference of her
circular path. Recall that circumference = 2πr. Thus,
total distance traveled = 2(2πr) = 2[2(π)(3 m)] = 37.68 m.
Total distance traveled 37.68 m
v= = = 7.54 m/s
time 5s
(b) Using the equation for centripetal acceleration, we obtain
v2 (7.54 m/s)2
ar = r = = 18.75 m/s2
3m

Example: In one model of the hydrogen atom, an electron orbits a proton in a circle of radius 5.28 ×
10−11 m with a speed of 2.18 × 106 m/s. (a) What is the acceleration of the electron in this
model? (b) What is the period of the motion?
Solution: (a) The electron moves in a circle with constant speed. It is accelerating toward the center of
the circle and the acceleration has magnitude
v2
ar = r
Substituting the given values,
v2 (2.18 × 106 m/s)2
ar = = = 9.00 × 1022 m/s2
r 5.28 × 10−11 m
(b) As the electron makes one trip around the circle of radius r, it moves a distance 2πr (the
circumference of the circle). If T is the period of the motion, then the speed of the electron is
given by the ratio of distance to time,
2πr
v=
T
Manipulating the formula to obtain the period, T, we have
2πr
T=
v
Substituting the given values, we get
2π(5.28 × 10−11 m)
T= = 1.52 × 10−16 s
(2.18 × 106 m/s)
The period of the electron’s motion is 1.52 × 10 −16 s.

[Grade 12 – Classical Physics I (Calculus Based)] 33

 Module 3 – Motion in 2 Dimensions and 3 Dimensions

LEARNING RESOURCES

References:
Halliday, David, Resnick, Robert, Walker, Jearl (2014) Fundamentals of Physics 10th
Edition. River Street, Hoboken, USA: John Wiley & Sons, Inc.
Silverio, Angelina A (2017) Exploring Life through Science Series General Physics 1.
Quezon City, Philippines: Phoenix Publishing House.
Centripetal force (nd). Show Me the Physics. Retrieved from
https://www.showmethephysics.com/home/notes/MotionPlane/centripetalForce.h
tm
Condition of Circular Motion (nd). Java Lab. Retrieved from
https://javalab.org/en/condition_of_circular_movement_en/
Projectile Motion (2019). People Highline. Retrieved from
https://people.highline.edu/iglozman/classes/physnotes/projectile.htm
Projectile Motion - PowerPoint PPT Presentation (2020). Slide Serve. Retrieved from
https://www.slideserve.com/santo/projectile-motion

For online exercises, you may visit the following links:

https://interactives.ck12.org/simulations/physics.html
https://phet.colorado.edu/en/simulation/moving-man

ABOUT MODULE

Module Author/Curator : Mr. Jomari B. Montalbo

Template & Layout Designer : Mr. Florence A. Somoria

[Grade 12 – Classical Physics I (Calculus Based)] 34