IJCRE

INTERNATIONAL JOURNAL OF CHEMICAL
REACTOR ENGINEERING
Volume 8 2010 Article A153
Deposition of Evaporating Droplets in a
Decelerating Boundary Layer with Wall
Suction: Mathematical Analysis
Roee Z. Orland
Rafael Tadmor
David Katoshevski
Ben-Gurion University of the Negev, orland@bgu.ac.il
Lamar University, rafael.tadmor@lamar.edu
Ben-Gurion University of the Negev, davidk@bgu.ac.il

ISSN 1542-6580
Copyright c 2010 The Berkeley Electronic Press. All rights reserved.
Deposition of Evaporating Droplets in a Decelerating
Boundary Layer with Wall Suction: Mathematical
Analysis
Roee Z. Orland, Rafael Tadmor, and David Katoshevski

Abstract
The problem of spray/droplets dynamics in a downstream decelerating bound-
ary layer accompanied by evaporation and wall suction is treated analytically.
A similarity approach is employed and explicit expressions are obtained for the
distribution of the host-gas velocity and for the distribution of the liquid phase.
Several options are considered in terms of evaporation, including the possibili-
ties of constant evaporation in the lateral direction of the boundary layer and of
evaporation dependent on proximity to the wall. The results reveal the possibility
that, under certain conditions, the liquid phase concentration reaches an extremum
inside the boundary layer domain, rather than at the wall or in the free stream.
KEYWORDS: boundary layer, similarity solution, two-phase ow
Please send correspondence to: David Katoshevski, Environmental Eng. Unit, Ben-Gurion Uni-
versity of the Negev, Beer-Sheva 84105, Israel; email: davidk@bgu.ac.il; tel. +972-503-9999-47.

Introduction

Droplet dynamics in general and, specifically, in boundary layers have various
industrial applications. The effect of droplet evaporation is of importance in
combustion facilities as well as in the paint industry, heat exchange facilities, and
pesticide spraying. Wall suction in two-phase flow has ramifications to sampling
systems in pipe and stack flows. The issue of droplet dynamics in boundary layers
and shear layers has gained little attention. The same for the case of a decelerating
spray flow. Adding to that an imposed wall suction, the outcome is a situation
which, to the best of our knowledge, has not been addressed mathematically.
The similarity solution for a boundary layer is a very well established
topic. Blasius (1908) introduced the solution for a boundary layer with a constant
free stream velocity. Falkner and Skan (1931) extended the approach to deal with
free stream velocity which behaves as a power of the longitudinal distance. In the
present work we address a decelerating boundary layer on a flat plate in which the
flow is described by the Falkner-Skan equation. A spray is introduced in that
boundary layer and suction is imposed, which affects both the flow field and the
liquid phase distribution.
It is important to note that the non-linearity of the equation for a
decelerating flow, leads to the fact that there is an infinite number of solutions
that obey the boundary conditions, and it is common to use the argument that the
solution which admits an exponential behavior towards the outer boundary
condition, should be chosen (Hartree, 1937). As deceleration increases, the
solution admits an overshoot in the velocity distribution, which is considered by
some researchers as non-physical (Hartree, 1937; Stewartson, 1954) and physical
by others (Libby and Liu, 1967). When in those cases suction is imposed, it
eliminates the overshoot and thus the solution is acceptable by all in the physical
sense. This is the case that we specifically elucidate here, where an added value of
that is the fact that it has an analytical solution, and thus can lead to useful
analytical expressions.

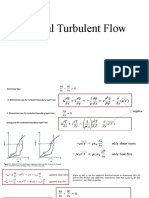
Development of the mathematical model

Hence, we represent the flow field near the wall in the boundary layer approach.
The free-stream longitudinal velocity is represented as

o
x U U =
(1)

where x is a normalized longitudinal distance, and U
is a characteristic
longitudinal velocity. At present we consider a decelerating flow, that is the power
1 Orland et al.: Deposition in a Decelerating Boundary Layer
Published by The Berkeley Electronic Press, 2010

o is negative although the formulation in general can handle acceleration as well
(o>0).
Using the conventional boundary layer normalization of the gas phase
continuity and momentum equations one obtains:

0 =
c
c
+
c
c
y
v
x
u
(2)
x
c
F
U
x
y
u
x
p
y
u
v
x
u
u
p
1
2 2
2
+
c
c
+
c
c
=
c
c
+
c
c
(3)

where u and v are the normalized gas velocity components in the x and y
directions, respectively, p is the normalized pressure and p is the mixture density.
F
x
describes the interaction-force between the gas and the aerosol particles. In the
frame of the current analysis we assume that the droplets are small enough to
follow the host gas streamlines, i.e. the velocity lag between the gas and the
droplet is negligible and we may neglect the interaction force-term.

Solving for the gas velocities

For the similarity approach we define the commonly used stream function + and
similarity variable n
( )
( )
( ) n o
o
f x
2 / 1
2 / 1
1
2
1
+
+ = + (4)
( )
( ) 2 / 1
2 / 1
1
2
1

+ =
o
o n x y (5)

which leads to the normalized similarity function for the velocity profile

' f U u = (6)
where prime denotes differentiation with respect to n. that is
n d
df
f = ' , and U is
the free-stream velocity.
The lateral velocity component is

|
.
|
\
|
+
+
|
.
|
\
| +
=

'
2
1
2
1
2
1
2 / ) 1 (
2 / 1
f f x v n
o o o
o
(7)

2 International Journal of Chemical Reactor Engineering Vol. 8 [2010], Article A153
http://www.bepress.com/ijcre/vol8/A153

The momentum equation in terms of the similarity variable has the Falkner-Skan
form:
( ) | | 0 ' 1
1
2
' ' ' ' '
2
=
+
+ + f ff f
o
o
(8)

As this is a well-established solution, we forego a more detailed derivation (a
detailed derivation is presented in many fluid mechanics books, such as Evans
(1968), Schlichting (2000)).
The term
1
2
+ o
o
, which was used by Falkner and Skan, (1931) is in itself a
constant, and shall hereto be replaced by | , as used by Hartree (1937), which has
become more common in boundary-layer literature.
The boundary conditions we employ at the wall, that is at y = 0 and 0 = n ,
are:

0 ' ) 0 ( '
0
= = f f (9)
0
) 0 ( f f = (10)

where the former is associated with the no-slip condition, and the latter with
suction velocity through the porous boundary. As we move away from the wall at

: + n
1 ' =
f (11)

signifying the finite thickness of the boundary layer.
A non-slip condition (Eq. 9) can be assumed at the solid-fluid interface for
certain systems, see for example Brenner (2009), typically depending on the
commensurability and relative strength of wall-fluid interaction (c.f. Thompson
and Troian, 1997). For a fluid that contains droplets, the no-slip condition is more
prevalent because once a droplet hits a surface, a three phase contact line is
formed, which acts to further increase the wall-liquid intermolecular interaction
(Tadmor et al 2009), and hence increase stagnation at the wall (no-slip) of the
fluid as a whole.
The behavior of the solution for the above momentum equation is very
sensitive to the value of the parameter o . For negative values of that parameter,
which represent flow deceleration (see Eq (1)), the boundary condition at the
outer region (Eq (11)) is satisfied regardless of the condition at the wall surface.
This form of behavior is discussed by Katoshevski et. al., (1993). As the solution

is thus non-unique, the common approach, as mentioned before, is to choose the
velocity profile that has an exponential behavior, and thus the boundary layer is
minimal in thickness, a condition known as the Hartree criterion (Hartree, 1937;
Rosenhead, 1963). This condition is based on a variational analysis of the
asymptotic behavior of a satisfactory solution, which showed that ' f must tend to
unity as rapidly as possible for continuity of solutions between
+
0 o and
0 o . Another feature of that equation for a decelerating flow velocity is the

appearance of an overshoot in the velocity profile, that is, ' f in some areas
becomes larger than unity, and this is subject to the value of
0
f (Eq. 10).
We now turn to present an analytical solution for a particular case of
interest.

Analytical solution for a particular case of downstream decelerating flow

For a specific case in which the flow decelerates in the form of
3 / 1
x , that is when
3
1
= o . an analytical solution may be obtained as a function of the suction
rate, or in other words as a function of the boundary condition at the surface
0
f f = (Eq. 10) representing the mechanism of mass transfer to the wall.
Next we present a particular analytical solution for the flow field. For
3
1
= o the momentum equation (Eq. 8) becomes

( ) 1 ' ' ' ' ' '
2
= + + f f f f (12)

This equation may be integrated twice:

Y f f f = + ' ' ' (13)
a Y f f 2
2
1
2
1
'
2 2
+ = + (14)

where Y=n+c, and c and a are constants whose values are to be determined.
Employing the boundary conditions at the surface in Eq. (13), one obtains:

c f =
0
' ' (16)

and from Eq. (14) :

2 / 1 2
0
) 4 ( a c f + = (17)

or ( ) a f c 4
2
0
= (where the condition of positive shear at the wall was used to
determine that c be taken as positive). Orland et al (2009) have demonstrated
that there is no physical or mathematical reason for f to attain only real values,
and it may in fact attain purely imaginary values (but not complex values, where
both real and imaginary components exist). However, as ' f is a ratio of velocities
and must be real, an imaginary value of f or ' ' f requires also that n be
imaginary. Thus, imaginary values require that o be smaller than -1, and as a
direct consequence 2 > | . As the current analysis holds only for 1 = | , we may
conclude that 0 4
2
> + a c (for f to be real-valued) and also for c to be real-
valued (as it is the boundary value of ' ' f ) . These combined result in the value of
a being larger than a real, non-positive number
4
2
c
.
The solution for Eq. (14) involves parabolic-cylinder functions
(Abramowitz and Stegun, 1972). For
2
1
= a it admits an exponential behavior
(Rosenhead, 1963), and this value, which is chosen on the basis of the principle of
minimal boundary layer thickness (referred to earlier), enables a uniqueness of the
solution, which is:

( )
|
.
|
\
|
+
|
.
|
\
|
+ =
Y
dS S k
Y
Y Y f
2
2
2
1
exp
2
1
exp 2
(15)

where k is a constant which is determined by the boundary conditions, and the
limits of integration are c , corresponding to the minimal value of Y, and c + n at
the particular point. Note that this choice also limits
0
f to values equal to or
greater than 2 .
Another option to determine the value of a is by comparing it to
measurements.
Thus, the constant c and the parameter
0
f are interconnected, and for a
known value of a determining one of them, say
0
f , as it is a measure of suction, a
characteristic of the flow which we may control, will lead to the value of the
other. This also leads to a value of the parameter k in the analytical solution, Eq.
(15).

From the no-slip condition we arrive at

( )
2
2 2
exp 2
2
1
exp
2 1 0
k
c k c c
dy
df
c y
+ |
.
|
\
|
= =
=
(16)

From which we may derive positive and negative values for k :

( )
|
.
|
\
|
+ + =
2 2
1
2
1
exp 2 c c c k (17a)
( )
|
.
|
\
|
+ =
2 2
2
2
1
exp 2 c c c k (17b)

However, as a negative value of k would guarantee that at certain values of n the
solution would produce an overshoot, we require that k be positive (eq. 17a).
Note that the same result would be achieved if, instead of a condition for
c Y
dY
df
=

we had used a condition for
c Y
f
=
.

Figure 1 - ' f as a function of n for different values of
0
f


Solving for the liquid-phase mass distribution in the boundary layer

We adopt the mono-sectional portrayal for description of the spray as previously
used by Katoshavski and Greenberg (2007).
The mass conservation for the spray, assuming droplets follow the
streamlines, is:

Q E
y
v
x
u
Q
y
Q
v
x
Q
u
~
=
c
c
+
c
c
+
c
c
+
c
c
(18)

where Q is the normalized mass fraction of liquid and E
~
is the evaporation
coefficient that may be a function of x and y.
Next we assume the following behavior for Q:

( ) n
o
q x Q= (19)

Experiments in jet flow, for example, have shown that centerline droplet
concentrations decrease by
1
x (Yule et al, 1982), and here we assume that inside
the boundary layer concentrations relative to the free stream are governed by the
same similarity principle as the flow field. Such a form of representation allows
us to implement, by a negative value of the power o. the fact that the amount of
particles decreases in the downstream direction.
In order to ensure that Q depends on the similarity variable only, it is
necessary to set

( ) n
o
E x E
1
~

= (20)

a relation necessary for the arrival at an ordinary differential equation. Not
unreasonably, Eq.(20) implies that the evaporation coefficient decreases as the
droplets move downstream. The significance of equation (20) is that the
evaporation coefficient E
~
takes on a particular functional dependence on the
similarity variable. However, such dependence may readily be attributed to the
way in which, in a realistic situation, local conditions of the flow field, ambient
temperature and gaseous composition, alter the evaporation rate of the droplets in
the spray. Clearly, this new solution is specific to such circumstances only.
However, if experimental data for E
~
is available, a series of best-fit correlations
for ( ) n E may be used. These will no doubt be affected by the accommodation
factor of the specific system in question, ambient and surface temperatures

(including possible downstream distribution) and the specific properties of both
phases, but these would result in variation of the best-fit functions used, and at
present we do not wish to limit these, although in the Results section we do
address specific rudimentary functions.
From Eq. (18) we thus obtain
( ) 0 ' 4 ' ) 1 ( 2 = + + q E f q f o o (21)
The boundary condition that the function q must satisfy is

) (
1
n q q = at ) (
1
< =n n

Where
1
n is the set of similar points at which we have information regarding the
concentration, e.g. 0
1
= n , signifying the boundary (as employed by Orland et al
(2009)),
v
n n =
1
, the set of points at which there is an appreciable onset of
evaporation (i.e. points where the droplets in the spray begin to reach their boiling
temperature; as employed by Katoshevski and Greenberg (2007)), or
n , i.e. the
points at the outer edge of the boundary layer.
Applying the boundary condition in a general form, we arrive at
( ) ( ) ( )
|
|
.
|
\
|
+
|
|
.
|
\
|
=

+
n
o n n
n
n
o
o
d
f
E
f
f
q
q
1
1
2
exp
1
2
1 1
(22)

For the case of no evaporation Eq. (22) is reduced to
( ) ( )
1
2
1 1
+
|
|
.
|
\
|
=
o
o
n n f
f
q
q
(23)

which converges with the solution derived by Orland et al (2009).
Away from the boundary, we may evaluate f as:
( )
|
.
|
\
|
+ + =
|
.
|
\
|
+
|
.
|
\
|
+ =
2
2
2
2
1
2
1
exp
2
1
exp 2
n n O c
dS S k
Y
Y Y f
Y

where ( ) 2
2
0
= f c , as discussed earlier.
This would be within 5% of the value of f for 54 . 1 > n .

If we were to consider cases for which n and
1
n are both larger than 1.54,
equation 22 would further reduce to
( )

+
|
|
.
|
\
|
+
+
~

n
n
o
n
n n
n
n
1
3 exp
3
1 1
d
c
E
c
c
q
q
(24)
Please note that as we assume that, to a first approximation, droplets follow the
gas streamlines, the normalized mass flux at the boundary would be
( ) = |
.
|
\
|
+
+
|
.
|
\
| +
= =
=
= 0
2 / ) 1 (
2 / 1
0
*
'
2
1
2
1
2
1
n
o o
n
o o o
f f x q x Q v j
y

2
1 2
2
1
+
+
=
o o
o
x (25)
We now turn to present an analysis of various features of the analytical solution.

Results and Discussion

In order to extract a solution to Eq. (22) and for illustrative purposes we consider
the particular flow field for which 3 / 1 = o , with different possible functions for
E . This is merely illustrative, and in physical situations experimental results for
E , not readily available to us, may be used to establish correlations. Moreover, in
real situations a single functional form of E may not be advised, but rather a
series of functions of the form:

( ) ( ) | | ( ) ( ) | |
( ) ( ) | |
n n n
E H H
E H H E H H E
n n n n
n n n n n n n
+
+ + =
1
2 2 1 1 1
...
...
(26)

Where H is the Heaviside step function,
n
n n n , ,
2 1
are points where the best-fit
function should be altered and
n
E E E , ,
2 1
are the best-fit functions for each
region.

Constant values of E

First, we employ 0 = E , which was the case presented by Orland et al (2009).
Figure (2) presents results for q in the similarity coordinate (a) and as contours in
the (non-dimensional) x-y plane (b). Figure (3) presents contours of Qin said x-y
plane. The maximum value of q is found at the wall.

Figure (2) Representation of q in two ways: (a) as a function of n , and (b) as
contours of constant value in the (non-dimensional) x-y plane, for
0 ,
2
1
,
3
1
= = = E o o


Figure (3) Contours of constant values of Q in the (non-dimensional) x-y plane,
for 0 ,
2
1
,
3
1
= = = E o o

For a larger constant value of E the trends are reversed (Figures (4,5))
and the value of q is increased with distance from the wall.


Figure (4) - q (a) as a function of n and (b) as contours of constant value in the
(non-dimensional) x-y plane, for 1 ,
2
1
,
3
1
= = = E o o


Figure (5) Contours of constant values of Q in the x-y (non-dimensional) plane,
for 1 ,
2
1
,
3
1
= = = E o o

Varying values of E

For thicker boundary layers, however, it is reasonable to assume that variation of
temperature away from the boundary (here we assume that the boundary is
warmer than the ambient fluid) will give rise to variations in E . As E is
constrained to being a function of n only, we next present two such cases, where
E decreases away from the boundary: n n =

E and ( ) n = exp E .
Figures (6,7) display results for n n =

E . Under this condition the
function q reaches a maximum at 362 . 2 ~ n . However, as this is close to the edge
of the boundary layer, it is not easily discerned from Fig. (6). Moreover, as the
negative value of o suggests a decrease in Q as x increases (and n decreases),
this extremum is further concealed.


(non-dimensional) x-y plane, for n n o o = = =

E ,
2
1
,
3
1


for n n o o = = =

E ,
2
1
,
3
1

Figures (8,9) display results for ( ) n = exp E . Under this condition the
function q reaches a maximum at 155 . 1 ~ n . As this extremum is located further
into the boundary layer than in the case of n n =

E , it affects the trends of q
and Q more appreciably.
Figure (10) displays contours of n which may be of assistance in
analyzing the results shown in figure (8). The contour of maximum concentration
inside the boundary layer is the contour of 15 . 1 = n , displayed in figure (10). To
avoid misunderstanding, we emphasize that figure (10) does not, in fact, present
any results of physical significance, but rather a map in cartesian coordinates of
the similarity variable, to assist the reader when attempting to correlate physical
results in the similarity plane to the physical plane.
Figure (9), which displays contours of actual concentration, accounts for
the negative effect of increasing downstream distance. Note that the entire region
addressed in all figures is within the boundary layer ( 84 . 2 s n ).

(non-dimensional) x-y plane, for ( ) n o o = = = exp ,
2
1
,
3
1
E

for ( ) n o o = = = exp ,
2
1
,
3
1
E

Figure 10 - n as contours of constant value in the (non-dimensional) x-y plane,
for
3
1
= o

Conclusions

An analytical solution for an evaporating spray in a boundary layer was presented,
incorporating a new analytical solution for the flow field at
3
1
= o with a
mass-conservation approach to a second, liquid phase. Additional parameters
were restricted to forms which allowed the solution to remain self-similar. It
should be noted that, as n is linearly dependent on y, at a given longitudinal
distance n changes linearly with distance from the boundary, and the dependence
on n and on y is essentially the same, with a stretching effect.
For decaying evaporation as we move away from the boundary a maximal
value of the concentration may be observed inside the boundary layer, which is a
phenomenon which warrants further experimental investigation.
These results may be of interest in combustion facilities, heat exchangers,
spraying of pesticides, predicting mist wetting a soil, spray-cooling systems for
super computers, chemical reactors where sedimentation is required (such as
heterogeneous-reaction processes) or other systems where a two-phase flow near
a surface is of interest.

Nomenclature

a Constant
c Constant
E
~

Evaporation coefficient
E
Part of E
~
only dependent on n
f Part of the stream function only dependent on n
' f
n d
df

0
f f at 0 = n
x
F Interaction force between gas and aerosol particles
*
j
Normalized mass flux at boundary
k Constant
p Normalized pressure
Q Normalized mass fraction
q
Part of Q only dependent on n
u Local longitudinal velocity
U Free stream velocity
U

Characteristic longitudinal distance

v Local lateral velocity
x Normalized longitudinal distance
y Normalized lateral distance
Y
c + n

Greek letters

+ Stream function
o Power by which free stream velocity changes downstream
|
1
2
+ o
o

o Power by which Q changes with downstream distance
n
Similarity variable
1
n Set of similar points at which we have information regarding the
concentration
v
n Set of points at which there is an appreciable onset of
evaporation
n Set of points at outer edge of the boundary layer

p
Fluid density

References

Abramowitz M, Stegun IA, Handbook of Mathematical Functions: with
Formulas, Graphs and Mathematical Tables, 1970, Dover Publications.

Blasius H, "Grenzschichten in Flussigkeiten mit Kleiner Reibung. (The Boundary
Layer in Fluids with Very Little Friction)", 1908, Zeit. Math. Phys. 56,1.

Brenner H, "A Nonmolecular Derivation of Maxwell's Thermal-Creep Boundary
Condition in Gases and Liquids via Application of the LeChatelier-Braun
Principle to Maxwell's Thermal Stress", Phys. Fluids, 2009, 21, 053602.

Evans HL, Laminar Boundary Layer Theory, 1968, Addison-Wesley

Falkner VM, Skan SW, "Some Approximations of the Boundary Layer
Equations", Philos. Mag. 1931, 12, 865.


Hartree DR, "On an Equation Occurring in Falkner and Skan's Approximate
Treatment of the Equations of the Boundary Layer", Proc. Camb. Phil.
Soc., 1937, 33, 223.

Katoshevski, D, Frankel I, Weihs D,"Viscous Interaction Between Parallel Radial
Streams", Fluid Dynamics Research, 1993, 12, 153.

Katoshevski D, Greenberg JB, "A New Solution for an Evaporating Spray in a
Shear Layer, Including Downstream Flow Deceleration/Acceleration,
Atomization Sprays, 2007, 17(7), 641.

Orland RZ, Broday D, Katoshevski D,"New Imaginary-valued Similarity
Solutions for Laminar Boundary Layers with Sprays", Atomization
Sprays, 2009, 19(12), 1111

Rosenhead L, Laminar Boundary Layers, Oxford University Press, 1963

Schlichting H, Boundary-Layer Theory, McGraw Hill, 1968

Stewartson K, "Further Solutions of the Falkner-Skan Equation, Proc. Camb.
Phil. Soc., 1954, 50, 454

Tadmor R, Bahadur P, Leh A, Nguessan HE, Jaini R, Dang L,"Measurement of
Lateral Adhesion Forces at the Interface between a Liquid Drop and a
Substrate", Phys. Rev. Lett., 2009, 103, 266101.

Thompson PA, Troian SM, "A General Boundary Condition for Liquid Flow at
Solid Surfaces, Nature, 1997, 389, 360.

Yule AJ, Seng CAH, Felton PG, Ungut A, Chigier N, A Study of Vaporizing
Fuel Sprays by Laser techniques, Combust Flame, 1982, 44, 71


IJCRE

Uploaded by

Copyright:

Available Formats

You might also like

IJCRE

Uploaded by

Document Information

Original Description:

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

IJCRE

Uploaded by

Copyright:

Available Formats

INTERNATIONAL JOURNAL OF CHEMICAL

Ben-Gurion University of the Negev, orland@bgu.ac.il

Lamar University, rafael.tadmor@lamar.edu

Ben-Gurion University of the Negev, davidk@bgu.ac.il

Roee Z. Orland, Rafael Tadmor, and David Katoshevski

0 o . Another feature of that equation for a decelerating flow velocity is the

n Set of points at outer edge of the boundary layer

You might also like