OAK INTERNATIONAL SCHOOL, BENIN Good luck!

Second Marking Period Examination 2022/2023

Subject: AP CALCULUS AB/BC

Name:……………………. Grade: 11 Date:…………. Duration: 2 ¼ HRS

PART A
MULTIPLE CHOICE QUESTIONS

INSTRUCTION: For each of the questions 1 to 16 in this part, write IN BLOCK LETTER the option
which corresponds to the correct answer in your answer booklet. SUBMIT YOUR QUESTION PAPER
ALONGSIDE YOUR ANSWER BOOKLET.

1. Select the FALSE statement C. 1 and III only

A. An instantaneous rate of change is a D. II and III only
function 3. If 𝑥 = 1 is the vertical asymptote and 𝑦 = −3
B. An instantaneous rate of change is the is the horizontal asymptote for the graph of the
same as a derivative function 𝑓 , which of the following could be
C. An instantaneous rate of change is the the equation of the curve?
slope of a tangent line −3𝑥 2
A. 𝑓(𝑥 ) =
𝑥−1
D. An instantaneous rate of change is the −3(𝑥−1)
B. 𝑓(𝑥 ) =
slope of a function 𝑥+3
−3(𝑥 2−1)
C. 𝑓(𝑥 ) =
(𝑥−1)2
2. Which of the following lines is an asymptote −3𝑥
D. 𝑓(𝑥 ) =
𝑥 2+5𝑥+6 (𝑥−1)2
of the graph of 𝑓 (𝑥 ) = ?
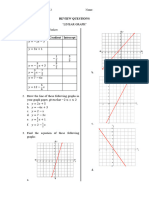
𝑥 2−𝑥−12

I. 𝑥=3 4. Determine the average rate of change of the

II. 𝑥=4 function 𝑦 = 3𝑥 on the interval [2, 4]
A. 2
III. 𝑦=1
B. – 2
A. II only C. – 3
B. III only D. 3
 9. The horizontal asymptote of the rational
3 ′ 2𝑥 2 −3𝑥+5
5. Given that 𝑓(𝑥 ) = −2𝑥 , determine 𝑓 (𝑥) function
A. −6𝑥 𝑥−1
A. is the line 𝑦 = 0
B. 6𝑥 2
B. does not exist
C. 6𝑥
C. is the line 𝑦 = 2
D. −6𝑥 2
D. is the line y = - 1

10. The vertical asymptote of the rational function

1
2𝑥−1
A. does not exist
B. is the line 𝑥 = 1
1
C. is the line 𝑥 =
2
1
6. The graph of the function 𝑓 is shown in the D. is the line 𝑥 = −
2
figure above. At how many points in the
interval 𝑎 < 𝑥 < 𝑗 is 𝑓′ not defined? 11. Given the function 𝑦 = 8, find 𝑦′
A. 3 A. 8𝑥
B. 4 B. – 8
C. 5 C. 1
D. 6 D. 0

12. Given that 𝑓(𝑥 ) = 1 − 2𝑥 − 𝑥 3 . Find 𝑓(−1)

7. Given the instantaneous rate of change A. 0
2 ln(1+ℎ)−0 B. – 3
lim , determine the 𝑥 −value of the
ℎ→0 ℎ
C. 4
instantaneous rate of change.
D. – 4
A. –1
B. 1 13. Given that 𝑓(𝑥 ) = 𝑥 − 6𝑥 3 , find 𝑓′(𝑥)
C. 0 A. −18𝑥 2
D. –2 B. 1 − 18𝑥 2
C. 18𝑥 2 − 1
8. Given the instantaneous rate of change D. 18𝑥 2
2(𝑥−2)2+3(𝑥−2)+1−(3)
lim , determine the 𝑥
𝑥→−2 𝑥+2
14. Evaluate lim
original function. 𝑥→0 𝑠𝑖𝑛𝑥
A. 𝑓(𝑥 ) = 2𝑥 2 − 3𝑥 − 3 A. 0
B. 𝑓(𝑥 ) = 𝑥 2 + 3𝑥 + 1 B. -1
C. 𝑓(𝑥 ) = 2𝑥 2 + 3𝑥 + 1 C. 1
D. 𝑓(𝑥 ) = 2𝑥 2 + 3𝑥 − 3 D. ∞
 Using the graph above, find the average rate of
change of 𝑓(𝑥) on the interval −2 ≤ 𝑥 ≤ −1.
15.
A. −3
B. 3
C. −2
D. 2
E.
16. Given that 𝑦 = cos(3 − 2𝑥) find 𝑦′
A. − sin(3 − 2𝑥)
B. 2 sin(3 − 2𝑥)
C. −2 sin(3 − 2𝑥)
D. Sin (3 − 2𝑥 )

PART B
THEORY
INSTRUCTION: Answer ALL questions in this part

1. Given the function 𝑓 (𝑥 ) = 1 − 5𝑥 − 𝑥 2

a) Find the average rate of change over the closed interval [1 , 3]
b) Instantaneous rate of change at x = 2

2. Given the table below:

𝑥 𝑓 (𝑥 ) 𝑓′(𝑥) 𝑔(𝑥 ) 𝑔 ′ (𝑥 )
3 7 2 1 6
4 −3 3 4 −2

𝑓(𝑥)−2𝑔(𝑥)
If ℎ(𝑥 ) = 𝑓 (𝑥 )𝑔(𝑥 ) − 4𝑓(𝑥) and 𝑝(𝑥 ) = , find
𝑓(𝑥)

a) ℎ′(3)
b) 𝑝′(4)
1
3. If ℎ(𝑥 ) = 𝑥 ∙ 𝑓 (𝑥 ) ∙ 𝑔(𝑥) , find ℎ′(1) if 𝑓(1) = −2, 𝑔(1) = 3, 𝑓 ′ (1) = 1 and 𝑔′ (1) = .
2
𝑥
4. Let 𝑔(𝑥 ) = . Find 𝑔′′(4)
√𝑥−1

5. Given that 𝑦 = 3𝑥 2 sin (4𝑥 − 1), find 𝑦′′(𝑥)

Good luck!