6 Statistics for mining engineering

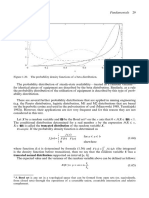
the values are real numbers and this function fulfils the above axioms. The probability is a
number for a fixed event. This approach is more general than the original one.
It is worth adding here that where the definitions of probability are concerned, there are
also some other theories dealing with probability, i.e. the theory of subjective probability
and Bayesian theory. The first theory formalises the personal assessment of the chances of
the occurrence of a given random event. In practical applications individuals assessing the
chances of this appearance are selected purposely by presuming that their estimation will be
significant, which is important because they have substantial knowledge in the case being
considered. The second theory applies two terms – a priori probability for the description of
knowledge about the investigated phenomenon before the investigation is done and a posteri-
ori probability for the description of enriched knowledge because the results of investigation
are known.
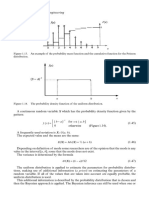
The conditional probability denoted by P(A|B) is the probability of the occurrence of event
A provided that event B has appeared (i.e. P(B) > 0). It is calculated as the quotient of the
joint probability of A and B and the probability of B6,7

P(A B )
P(A | B ) = (1.7)
P(B )

The probability of the sum of two events A and B

P(A ∪ B) = P(A) + P(B) – P(A ∩ B) (1.8)

We say that the random variable A is stochastically independent8 of an event B if

P(A|B) = P(A) (1.9)

This means that the occurrence of one does not affect the probability of the other. The
concept of independence extends to any dealing with collections of more than two events or
random variables.
Considering the above, we can easily see that for two independent events the following equa-
tion holds:

P(A ∩ B) = P(A) P(B) (1.10)

Remark. Events can be pairwise independent but simultaneously jointly dependent.

Consider a set {A1, A2, …, Ak} of pairwise disjoint events whose union is the entire space.
For any event B of the same probability space, the following relation holds:
k
P ( B ) = ∑ P ( Ai ) P ( B | Ai ) (1.11)
i =1

This is the formula for the total probability.

6
This is the so-called classical Kolmogorov definition. A different approach was presented by Bruno de
Finetti who preferred to introduce conditional probability as an axiom of probability.
7
Notice, that if for a certain event B, the corresponding P(B) = 0, the expression P(A|B) is undefined.
Nevertheless, it is possible to define a conditional probability with respect to a σ-algebra of such events
(such as those arising from a continuous random variable).
8
The following terms can be found in the literature: statistically independent, marginally independent
or absolutely independent.

Book.indb 6 12/9/2013 12:21:52 PM