Fundamentals 15

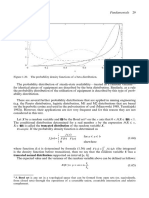
function are different. However, because the availability of actually constructed machines is
high as a rule and their utilisation also, thus the probability distribution that is applied has
a negative skew and the positions of the mode, median and mean is opposite to the one in
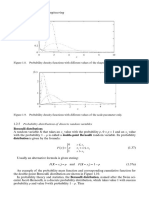
Figure 1.5. An example of the probability distribution of the utilisation of a hoist is shown
in Figure 1.6.
The last term that will be defined in this chapter is a class of probability distributions.
A class of probability distribution creates a family of distributions that have the same
cumulative function (or mass/density function) but whose structural parameters can be
different.
The parameters of probability density functions can be divided into three groups:
• location parameters
• shape parameters
• scale parameters.
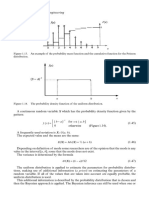
If there is a change in the value of the location parameter, the probability density function
is displaced along the x axis (Figure 1.7).
If there is a change in the value of the shape parameter, the probability density function
changes its profile (Figure 1.8).
A change in the value of the scale parameter makes the probability density function fatter
or causes it to be raised up (Figure 1.9).
A function of a random variable is a random variable as well.
Let us review some of the most frequently applied probability distributions in mining
engineering.

4
3.5
3
f.X(x) 2.5
2
1.5
1
0.5
0.5 0.6 0.7 0.8 0.9 1.0
x E(X) Mo(X)
Me(X)

Figure 1.6. Probability density function of the utilisation of a hoist; Mo(X) > Me(X) > E(X).

0.04

0.03
f(x)
f1(x) 0.02

0.01

0
0 50 100 150
x

Figure 1.7. Two probability density functions with different values of the location parameter only.

Book.indb 15 12/9/2013 12:22:05 PM