22 Statistics for mining engineering

0.5 f(x)

0.4 ξ≤1

0.3

0.2
ξ>1

0.1

x
0
0 2 4 6 8 10 12 14 16 18 20

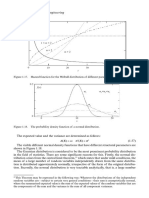
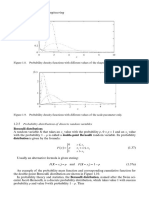
Figure 1.15. Gamma probability density functions.

If the scale parameter is not larger than 1, the distribution is extremely asymmetric.
Different shapes of the gamma probability distribution are shown in Figure 1.15.
The gamma distribution is applied to describe the load and strength of some machine ele-
ments (Warszyński 1988). It is also employed for the modelling of the lifetime of items that
are subject to cumulating agents. It is suitable for modelling the processes of the wearing of
the elements of machines and devices (Gertzbah and Kordonsky 1966).
In mining, winders have probability distributions of times of work and repair states that
can be satisfactorily described by the gamma distribution. The repair time of dumpers used
in open pit mines as well as of power shovels can be described by this distribution. The
gamma distribution is frequently applied in the mathematical description of the processes of
the wearing of tyres.
This probability distribution was also applied in the study of the processes of the sepa-
ration of grains in pulsators. It was assumed that the length of a single jump of a particle
during water pulsation is a random variable of the gamma distribution (Smirnow 1979).
The application of a generalised gamma distribution for the approximation of the composi-
tion functions for grains was presented by Nipl (1979). Some particular cases of the gamma
distribution have been used in the description of certain material characteristics during ore
enrichment processes (vide: Tumidajski and Saramak 2009 p. 63).
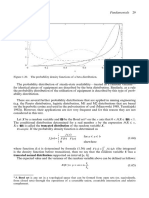
If the shape parameter is 1 in the gamma distribution, then the probability density func-
tion is given by the formula
(1.52)
f ( x ) = νe − νx ν>0

and this distribution is called an exponential distribution (Figure 1.16).

This probability distribution has many applications in engineering practice because it is
easy to use. Many electric and electronic parts have a lifetime probability distribution of an
exponential character. When the first models of the processes of the changes of states for
technical objects occurred in literature, they were almost exclusively composed of exponen-
tial random variables. The processes of changes of states in which the times of the states are
mutually independent and described by exponential distributions are called Markov proc-
esses. Their parameters and characteristics are shown in an explicit form, which is easy to
use. For this reason, exponential distribution was widely applied during the early days of
reliability development as well as in the theory of the exploitation of premature growth. This
distribution was abused in those days, but excuses can be found in the poor development
of advanced modelling by applying other, more complicated distributions. In those days,

Book.indb 22 12/9/2013 12:22:15 PM