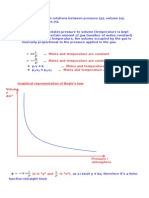
Thermal Equation of Stat for perfect gases

Theory Recap

Analytical expression of the thermal equation of state for

perfect gases:

a) pV = mRT , valid for m [kg] of gas

where p = absolute pressure of the gas [Pa];
V = volume of the gas [m3];
T = temperature of the gas [K];
m = mass of the gas [kg];
RM  J 
R= is the specific or gas constant
M  kgK 
J
with - RM = 8314,23 – universal (molar) constant
kmolK

- M – molar mass of the gas, i.e.:

kg kg kg
M O2 = 32 M = 44 M = 18
kmol ; kmol ; kmol ; etc.
CO2 H 2O

OBS: we will consider RM = 8315 J/(kmol K))

b) pv = RT , valid for 1 kg of gas

𝑉 𝑚3
where 𝑣 = 𝑚 [ 𝑘𝑔 ] = specific volume of the gas.
c) p = RT , equivalent of c), but expressed with density
m  kg 
where = = gas density.
V  m 3 

d) pV = n M RM T , valid for nM [kmol] of gas

m
where nM = kmol  = number of kmol.
M

e) pVM = RM T
V  m3 
where VM =   = molar volume.
nM  kmol 

f)Thermal equation of state applied in the normal state:

pNVN = mRTN

The normal state is defined by reference values of pressure

and temperature:
𝑝𝑁 = 760𝑚𝑚𝐻𝑔 = 1.013𝑏𝑎𝑟 = 1.013 × 105 𝑃𝑎
{
𝑇𝑁 = 273.15𝐾

The molar volume in the normal state has the same

value for any gas:
𝑅𝑀 𝑇𝑁 8315 ⋅ 273.15
𝑝𝑁 𝑉𝑀,𝑁 = 𝑅𝑀 𝑇𝑁 ⇒ 𝑉𝑀,𝑁 = =
𝑝𝑁 1.013 ⋅ 105
3
𝑚𝑁
= 22.414
𝑘𝑚𝑜𝑙