MODULE 8: RESISTANCE, INDUCTANCE, & CAPACITANCE

- current lags, while the voltage leads

OUTLINE A Voltage-current relation for an inductor in the a. time
I. Resistance domain, b. frequency domain
II. Inductance
III. Capacitance
IV. Voltage and Current Relationship
V. Impedance and Admittance
a. Impedance
b. Impedance in Rectangular Form
i. Example 1
c. Admittance
d. Conductance, Susceptance, and Admittance
VI. Types of Series Circuit
a. Series R-L
b. Series R-C
c. Series L-C
If it will be graphed
d. Series R-L-C
i. Example

RESISTANCE
AC through purely resistive circuit
-means that the current and voltage are in phase
The behavior of pure resistor in an AC Circuit is exactly similar
to that DC Circ
The voltage-current relations for a resistor in the a. time
domain, b. frequency domain

It shows that the current lags

CAPACITANCE
A perfect CAPACITOR in AC Circuit takes current that lead
the impressed voltage by exactly 90 electrical degrees.
-current leads
Voltage-current relations for a capacitor in the a. time
domain, b. frequency domain

If it will be graphed, then:

If it will be graphed

They contains same angle.

INDUCTANCE
A pure INDUCTOR in an AC Circuit takes current that lags
behind the impressed voltage by exactly 90 electrical degrees.
-a circuit contains an inductor

PALAYPAYON 1. POMAREJOS 2. SADSAD 3. SISON 4. TOLENTINO 5. | BIOE 2101 1

 Where x can be used as XL or Xc; Xc will be ued since it is the
one in series

𝑍 = 𝑅 + 𝑗𝑋𝑐

𝑍 = 5 + 𝑗(377)(50 𝑥 10−3 )

𝑍 = 5 + 𝑗18.85Ω
Convert it into polar form
𝑍 = 19.5019∠75.1443𝑜 Ω
ADMITTANCE
The current leads It is sometimes convenient to work with the reciprocal of
VOLTAGE AND CURRENT RELATIONSHIPS impedance, known as admittance
The admittance Y is the reciprocal of impedance, measure in
Element Z (Z=R + jx) Time Frequency siemens (S)
Domain Domain The admittance Y of an element (or a circuit) is the ratio of
R R 𝑉 = 𝑅𝑖 V = RI the phasor current through it to the phasor voltage across it, or
L 𝑗𝜔𝐿 𝑑𝑖 𝑉 = 𝑗𝜔𝐿𝐼 1
𝑣=𝐿 𝑌=
𝑑𝑡 𝑍
C 1 𝑑𝑣 1 Or
𝑖=𝐶 𝑉=
𝜔𝑐 𝑑𝑡 𝑗𝜔𝑐 𝐼
𝑌=
𝑉
IMPEDANCE AND ADMITTANCE As a complex quantity, we may write Y as
IMPEDANCE 𝑌 = 𝐺 + 𝑗𝐵
Frequency Formula Where:
𝑉 1 1
𝑍= 𝐺 = and 𝑗𝐵 =
𝐼 𝑅 𝑥
Z is a frequency-dependent quantity known as impedance, Therefore:
measured in ohms. 1
𝐺 + 𝑗𝐵 =
𝑅 + 𝑗𝑋
𝑉 = 𝑍𝐼 CONDUCTANCE, SUSCEPTANCE, AND ADMITTANCE
The impedance represents the opposition that the circuit
exhibits to the flow of sinusoidal current. Although the Conductance Susceptance Admittance
impedance is the ratio of two phasors, it is not a phasor, because Reciprocal of Reciprocal of Reciprocal of
it does not correspond to a sinusoidally varying quantity. Resistance Reactance Impedance
IMPEDENCE IN RECTANGULAR FORM Symbol is G Symbol is B Symbol is Y
As a complex quantity, the impudence may be expressed in 1 1 1
rectangular form as: 𝐺= 𝐵= 𝑌=
𝑅 𝑋 𝑍
𝑍 = 𝑅 ± 𝑗𝑋 Unit is Siemens Unit is Siemens Unit is Siemens
Where R = Re Z is the resistance and X = Im Z is the
reactance. The reactance, X, is just a magnitude, a positive
TYPES OF SERIES CIRCUIT
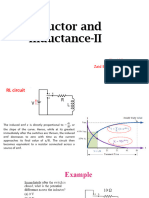
SERIES R-L
value, but when used as a vector, a j is associated with
Inductive is always lagging
inductance and a −j is associated with capacitance. Thus,
impedance Z = R + jX is said to be inductive or lagging since Total impedance of the circuit:
current lags voltage, while impedance Z = R − jX is capacitive or 𝑍 = 𝑅 ± 𝑗𝑋
leading because current leads voltage. 𝑍 = 𝑍∠𝜃
The impedance, resistance, and reactance are all measured
in ohms. The impedance may also be expressed in rectangular 𝑍𝑡 = √𝑅 2 + 𝑋𝐿 2
or polar form as Total supply voltage:
𝑍 = 𝑅 ± 𝑗𝑋 𝐸 2 = 𝐸𝑅 2 + 𝐸𝐿 2
Converting into polar form: Voltage drop across the resistor (volt)
|𝑍|∠𝜃
𝐸𝑅 = 𝐼𝑡 𝑅
Where
±𝑋 Voltage drop across the inductor (volt)
|𝑍| = √𝑅2 + 𝑋 2 , 𝜃 = 𝑡𝑎𝑛−1 𝐸𝐿 = 𝐼𝑡 𝑋𝐿
𝑅
And Total Supply Voltage
𝑅 = |𝑍| 𝑐𝑜𝑠𝜃, 𝑋 = |𝑍| 𝑠𝑖𝑛𝜃
𝐸𝑡 = √(𝐸𝑅 )2 + (𝐸𝐿 )2
EXAMPLE 1: Total current drawn:
𝐸𝑡
A resistance of 5Ω is connected in series with a 50mH inductor, 𝐼𝑡 =
find the impendence of the circuit; use w=377 𝑍𝑡
Solution: Power Factor = cosθ
𝑉𝑅 𝐼𝑅 𝑅 𝑃
Series RL circuit: 𝑃. 𝑓 = = = =
𝑉 𝐼𝑍 𝑍 𝑆
𝑍 = 𝑅 ± 𝑗𝑋 SERIES R-C
Voltage

PALAYPAYON 1. POMAREJOS 2. SADSAD 3. SISON 4. TOLENTINO 5. | BIOE 2101 2

 𝑉 2 = 𝑉𝑅 2 + 𝑉𝐶 2
Total impedance of the circuit: 𝑍1 = 50 + 𝑗(337)(150 𝑥 10−6 )
𝑍 = 𝑅 − 𝑗𝑋 𝑍1 = 50 + 𝑗56.55
𝑍 = 𝑍∠𝜃
1
𝑍𝑡 = √𝑅2 + 𝑋𝐶 2 𝑍2 = −𝑗[ ]
377(50 𝑥 10−6
Voltage drop across the Capacitor 𝑍2 = −𝑗53.0504
𝐸𝐶 = 𝐼𝑡 𝑋𝐶
Total supply voltage: 𝑍𝑇 = [(𝑧1 )−1 + (𝑧2 )−1 ]
𝐸𝑡 = √(𝐸𝑅 )2 + (𝐸𝐶 )2 𝑍𝑇 = [(50 + 𝑗56.55)−1 + (−𝑗53.0504)−1 ]
Total current drawn: 𝑍𝑇 = 56.0125 + 𝑗56.9708
𝐸𝑡 Transforming into polar form
𝐼𝑡 = 𝑍𝑇 = 79.8942∠−45.48𝑜
𝑍𝑡
Power Factor = cosθ Solving 𝐼𝑇
𝑉𝑅 𝐼𝑅 𝑅 𝑃 𝑉𝑠
𝑃. 𝑓 = = = = 𝐼𝑙 (𝑡) =
𝑉 𝐼𝑍 𝑍 𝑆 𝑍𝑇
Leading 100∠30𝑜
𝐼𝑙 (𝑡) =
Reactive Factor: 79.8942∠−45.48𝑜
𝑉𝐶 𝐼𝑋𝐶 𝑋𝐶 𝑄 𝐼𝑙 (𝑡) = 1.2517∠75.4860 Ω
𝑠𝑖𝑛θ = = = = 𝐼𝑙 (𝑡) = 1.2517 sin(377𝑡 + 75.4860) 𝐴
𝑋 𝐼𝑍 𝑍 𝑆
SERIES L-C
Total impedance of the circuit:
𝑍𝑡 = (𝑋𝐿 − 𝑋𝐶 )
Voltage drop across the inductor
𝐸𝐿 = 𝐼𝑡 𝑋𝐿
Voltage drop across the Capacitor:
𝐸𝐶 = 𝐼𝑡 𝑋𝐶
Total supply voltage:
𝐸𝑡 = (𝐸𝐿 − 𝐸𝐶 )
Total current drawn:
𝐸𝑡
𝐼𝑡 =
𝑍𝑡
Case 1: if 𝑋𝐶 > 𝑋𝐿
𝐸 = 𝐸𝐶 − 𝐸𝐿
𝑍 = 𝑋𝐶 − 𝑋𝐿
Case 2: if 𝑋𝐶 < 𝑋𝐿
𝐸 = 𝐸𝐿 − 𝐸𝐶
𝑍 = 𝑋𝐿 − 𝑋𝐶
SERIES R-L-C
Total impedance of the circuit:
𝑍𝑡 = √𝑅2 + (𝑋𝐿 − 𝑋𝐶 )2
Voltage drop across the resistor (volt)
𝐸𝑅 = 𝐼𝑡 𝑅
Voltage drop across the inductor (volt)
𝐸𝐿 = 𝐼𝑡 𝑋𝐿
Voltage drop across the Capacitor
𝐸𝐶 = 𝐼𝑡 𝑋𝐶
Total supply voltage:
𝐸𝑡 = √(𝐸𝑅 )2 + (𝐸𝐿 − 𝐸𝐶 )2
Total current drawn:
𝐸𝑡
𝐼𝑡 =
𝑍𝑡
EXAMPLE :
A coil of 50 ohms resistance and of 150 mH inductance is
connected in parallel with a 50 uF capacitor. The source voltage
is 100 sin (377t + 30 degrees). What is the equation of the line
current?
Solution
𝑉𝑆 = 100∠30𝑜
𝑉(𝑡) = 𝑉𝑚 sin 𝜔𝑡 + 0
𝑉(𝑡) = 100 sin 377 + 30𝑜

PALAYPAYON 1. POMAREJOS 2. SADSAD 3. SISON 4. TOLENTINO 5. | BIOE 2101 3