Professional Documents
Culture Documents
Math1314 5.1
Math1314 5.1
Uploaded by
Azizah IslamiyahOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Math1314 5.1
Math1314 5.1
Uploaded by
Azizah IslamiyahCopyright:
Available Formats
Section 5.
1 Polynomial Functions and Models
Term:
A term is an expression that involves only multiplication and/or division with constants
and/or variables.
A term is separated by ‘+’ or ‘–’
Polynomial:
A polynomial is a single term or the sum of two or more terms containing variables
with whole number exponents
A polynomial is a monomial or the indicated sum or difference of monomials
A Monomial is a polynomial that has exactly one term
A Binomial is a polynomial with two terms
A Trinomial is a polynomial with three terms
Coefficient: A number written next to a variable indicates multiplication.
Leading Coefficient is the coefficient of the term of the largest degree
Degree of a Polynomial is the greatest degree of all the terms of the polynomial
Degree of a nonzero constant term is 0
The constant ‘0’ has no defined degree.
Examples
Number Types Degree
Leading
Expression Of Of Of
Coefficient
Terms Polynomial Polynomial
2 1 Monomial 0
–2 1 Monomial 0
2x 1 Monomial 1 2
–2x 1 Monomial 1 –2
–53x3 1 Monomial 3 –53
4x + x3 2 Binomial 3 1
4 2 Binomial 4 –1
5 7 3 Trinomial 3 5
1
2 Not Polynomial since the exponent is not whole #
3
4 2 Not Polynomial since the exponent 2 is not whole #
2
3 2 1 3 Not Polynomial since the exponent is not whole #
3
0 1 Monomial Undefined
Definition of a Polynomial function:
A polynomial function is a function that can be written in the form of
⋯ 0
, where , , , are real numbers and is nonnegative integer. The number is
the leading coefficient, the coefficient of the variable to the highest power. The degree of the
polynomial function is .
Cheon-Sig Lee Page 1
Section 5.1 Polynomial Functions and Models
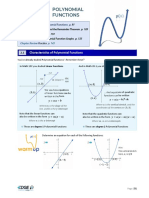
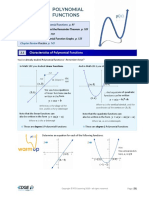
End Behavior of Polynomial Functions
⋯ 0
If the Degree of a polynomial function is Odd,
, leading coefficient, is POSITIVE , leading coefficient, is NEGATIVE
The graph falls left and rises right The graph rises left and falls right
If the Degree of a polynomial function is Even,
, leading coefficient, is POSITIVE , leading coefficient, is NEGATIVE
The graph rises left and right The graph falls left and right
Power Functions
A power function of degree is a monomial function of the form , where
is a none-zero real number and is a positive integer.
Turning Points
If is a polynomial function of degree , then has at most 1 turning points
If the graph of has 1 turning points, the degree of is as least .
Zeros of Polynomial Functions
The zero of polynomial function is the values of x for which is equal to 0.
If is a function of a real number for which , then is called a real zero of .
The following statements are equivalent
is a real zero of a polynomial function .
is an x-intercept of the graph of .
is a solution to the equation 0.
is a factor of .
Multiplicity
Multiplicities of Zeros
Zero
If is even, then the graph touches the x-axis and turns around at .
If is odd, then the graph crosses the x-axis at .
Cheon-Sig Lee Page 2
Section 5.1 Polynomial Functions and Models
Real Zeros and Factors of a function
For a real number leading coefficient and real zeros , , ⋯ , of a function
If the multiplicities of real zeros are , ,⋯, respectively, then the factor form of the
function is
⋯
Finding Zeros of Polynomial Functions
Method 1: Factoring by hand to find zeros
Method 2: Using a graphing calculator to find zeros of polynomial functions.
TI-83: Y= > ⋯ > 2nd MODE > 2nd TRACE > 2: ZERO
TI-83: Y= > ⋯ > 2nd GRAPH
TI-89: F2 > 2: Solve ⋯ 0,
Intermediate Value Theorem for Polynomial Functions
Let be a polynomial function with real number coefficients. If and have
opposite signs, then there is at least one value of between and for which 0.
Exercises
1. (Solution 1)
The factor form of a polynomial is
⋯
The leading coefficient 1.
Real zeros 1, 0, 2.
1 because the number of
zeros is equal to the degree of the polynomial.
1 1 0 2
1 2
2. (Solution 2)
The factor form of a polynomial is
⋯
1, 2, 1, 3, 4
1 because the number of zeros
is equal to the degree of the polynomial.
1 2 1 3 4
2 1 3 4
3. (Solution 3)
The factor form of a polynomial is
⋯
1, 9, 1, 3, 2
1 9 3
9 3
Cheon-Sig Lee Page 3
Section 5.1 Polynomial Functions and Models
4.
(Solution 4.a)
If is a factor of a polynomial function , is a zero of multiplicity of .
8 0→ 0 ⇒ the zero is 8 and the multiplicity of 8 is 1.
4 0→ 4 ⇒ the zero is 4 and the multiplicity of 4 is 2.
(Solution 4.b)
Because the larger zero is 8 and its multiplicity is odd, the graph crosses the x-axis at the larger x-intercept.
Because the smaller zero is 4 and its multiplicity is even, the graph touches the x-axis at the smaller x-intercept.
(Solution 4.c)
The maximum number of turning points is one less than the degree of the polynomial.
Because the degree of the function is 3, the maximum number of turning points is 3 1 2
(Solution 4.d)
The graph of the polynomial ⋯ resembles the graph of .
The degree of 7 8 4 is 3. Thus, its graph resembles the graph of 7 .
5.
(Solution 5.a)
49 0 → the solution to 49 0 is not real number
2 0→ 2 ⇒ the zero is 2 and its multiplicity is 3
Cheon-Sig Lee Page 4
Section 5.1 Polynomial Functions and Models
Question 5 continued…
(Solution 5.b)
Because the multiplicity of 2 is odd, the graph crosses the x-axis at the larger x-intercept.
(Solution 5.c)
49 → Degree is 2; 2 → Degree is 3. Therefore, 8 49 2 → Degree is 5
Because the degree of the function is 5, the maximum number of turning points is 5 1 4.
(Solution 5.c)
The degree of 8 49 2 is 5. Thus, its graph resembles the graph of 8 .
6.
(Solution 6.a)
0→ 0 ⇒ the zero is 0 and its multiplicity is 2.
7 0→ √7 √7 0⇒ √7, √7 ⇒ zeros are √7 and √7 .
The multiplicity of √7 is 1. The multiplicity of √7 is 1.
(Solution 6.b)
Because the largest x-intercept is √7 whose multiplicity is odd, the graph crosses the x-axis at the point.
Because the middle x-intercept is 0 whose multiplicity is even, the graph touches the x-axis at the point.
Because the smallest x-intercept is √7 whose multiplicity is odd, the graph crosses the x-axis at the point.
(Solution 6.c)
→ Degree is 2; 7 → Degree is 2. Therefore, 7 7 → Degree is 4
Because the degree of the function is 5, the maximum number of turning points is 4 1 3.
(Solution 6.d)
The degree of 7 7 is 4. Thus, its graph resembles the graph of 7
Cheon-Sig Lee Page 5
You might also like
- The Big Book Comes Alive (Transcribed)Document151 pagesThe Big Book Comes Alive (Transcribed)briespot100% (2)
- St. Augustine Choir Booklet-1Document255 pagesSt. Augustine Choir Booklet-1Henry Kaweesa97% (58)
- Lesson 1 First Among Equals Equations UnitDocument20 pagesLesson 1 First Among Equals Equations Unitapi-2618943550% (1)
- Sac Training Guide 2019 Final PDFDocument49 pagesSac Training Guide 2019 Final PDFArmando Santos100% (1)
- Algebraic ExpressionsDocument6 pagesAlgebraic ExpressionsCaitlene Lee UyNo ratings yet
- SAP FICO MaterialDocument24 pagesSAP FICO MaterialNeelam Singh100% (1)
- Title Card Guide Card Activity Card Assessment Card Enrichment Card Answer CardDocument39 pagesTitle Card Guide Card Activity Card Assessment Card Enrichment Card Answer CardAllen Abegando BitterNo ratings yet
- Na U3m07l01Document12 pagesNa U3m07l01Ateeq RehmanNo ratings yet
- Module 2, Lsseon 3Document8 pagesModule 2, Lsseon 3alayca cabatanaNo ratings yet
- Adding and Subtracting Polynomials 7.1: Essential QuestionDocument8 pagesAdding and Subtracting Polynomials 7.1: Essential QuestionMatematika SsvNo ratings yet
- College Algebra Tutorial 35: Graphs of Polynomial FunctionsDocument26 pagesCollege Algebra Tutorial 35: Graphs of Polynomial Functionssalman saeedNo ratings yet
- Writing in Math: Divine Word College of Legazpi Junior High School Department Legazpi CityDocument3 pagesWriting in Math: Divine Word College of Legazpi Junior High School Department Legazpi CityB E L ANo ratings yet
- PolynomialDocument6 pagesPolynomialuzairsofiNo ratings yet
- Chapter 2 - Polynomial Functions (Sample)Document62 pagesChapter 2 - Polynomial Functions (Sample)Math 30-1 EDGE Study Guide Workbook - by RTD LearningNo ratings yet
- 2.1 - Characteristics of Polynomial Functions Math 30-1Document14 pages2.1 - Characteristics of Polynomial Functions Math 30-1Math 30-1 EDGE Study Guide Workbook - by RTD LearningNo ratings yet
- Algebraic ExpressionsDocument6 pagesAlgebraic ExpressionsCaitlene Lee UyNo ratings yet
- Concept MapDocument1 pageConcept Mapapi-558321133No ratings yet
- Algebra 2 - Journal - Quarter 1Document54 pagesAlgebra 2 - Journal - Quarter 1somaya bakrNo ratings yet
- 1 Las M10 Week 1Document10 pages1 Las M10 Week 1Alma Delos ReyesNo ratings yet
- Polynomial FunctionsDocument31 pagesPolynomial FunctionsAdnan BukhariNo ratings yet
- Parts of An Algebraic Expression: Learn About The MathDocument4 pagesParts of An Algebraic Expression: Learn About The MathJhairah's ChannelNo ratings yet
- Harmonic Sequence: Reviewer By: S.Santos and J.Flores (Review Also Your Quizzes, Notes, PPT, and Recorded Lessons)Document2 pagesHarmonic Sequence: Reviewer By: S.Santos and J.Flores (Review Also Your Quizzes, Notes, PPT, and Recorded Lessons)scrthhNo ratings yet
- 5.1 Roots of A EquationDocument30 pages5.1 Roots of A EquationSATHIASEELAN SIVANANDAM, AdvocateNo ratings yet
- WEEK 1 Concept of PolynomialDocument8 pagesWEEK 1 Concept of PolynomialAngelo Rey NavaNo ratings yet
- Smp08alg Na Te2 C11 L04 11Document5 pagesSmp08alg Na Te2 C11 L04 11Fatima Fe VillamorNo ratings yet
- Factoring Polynomials Factoring Polynomials Factoring PolynomialsDocument11 pagesFactoring Polynomials Factoring Polynomials Factoring PolynomialsxxxxNo ratings yet
- 4 Polynomial ExpressionsDocument14 pages4 Polynomial ExpressionstaeNo ratings yet
- Logarithmic FunctionDocument22 pagesLogarithmic FunctionAngel Grace Delacerna DelicanoNo ratings yet
- Algebra +polynomial +LEDocument6 pagesAlgebra +polynomial +LEGaurav Kumar SinghNo ratings yet
- Polynomials Reviewer RevisedDocument24 pagesPolynomials Reviewer RevisedErica SantoniaNo ratings yet
- Lesson 3 - Algebraic Expression - PolynomialsDocument22 pagesLesson 3 - Algebraic Expression - PolynomialsShaineNo ratings yet
- Math Bridging TransesL2Document3 pagesMath Bridging TransesL2Ara Belle PonceNo ratings yet
- Introduction To Rational FunctionDocument75 pagesIntroduction To Rational FunctionJose Manga Jr.No ratings yet
- Degree of PolynomialDocument8 pagesDegree of Polynomialapi-127466285No ratings yet
- Quarter 2 Session 2part 2 Behavior of Graph of PFDocument21 pagesQuarter 2 Session 2part 2 Behavior of Graph of PFDale DelimNo ratings yet
- GM Reviewer Q1Document2 pagesGM Reviewer Q1Tricia BaltazarNo ratings yet
- 1-Polynomials TheoremsDocument35 pages1-Polynomials Theoremsm.lenasanz.c.sNo ratings yet
- ElemukilDocument11 pagesElemukilsriramxerox54No ratings yet
- Polynomial FunctionsDocument29 pagesPolynomial FunctionsJessel PalermoNo ratings yet
- 756639Document9 pages756639Jerry DNo ratings yet
- Quarter 2 Lesson 1 Illustrate Polynomial Functions Read Only1Document22 pagesQuarter 2 Lesson 1 Illustrate Polynomial Functions Read Only1Ramil J. MerculioNo ratings yet
- Math 10 FinalsDocument2 pagesMath 10 FinalsKrystel MamarilNo ratings yet
- ALGEBRAIC EXPRESSIONS. HandoutsDocument4 pagesALGEBRAIC EXPRESSIONS. HandoutsROBBGENO PADINASNo ratings yet
- Q2 MathDocument54 pagesQ2 MathPola WDNo ratings yet
- MODULE 04 - Equations of Order One - Homogeneous Differential EquationsDocument10 pagesMODULE 04 - Equations of Order One - Homogeneous Differential Equations2022310707No ratings yet
- PreCalculus Fall 2012 Lesson 021 - End Behavior of Polynomial FunctionsDocument3 pagesPreCalculus Fall 2012 Lesson 021 - End Behavior of Polynomial FunctionsROSA LAGRIMASNo ratings yet
- Logarithmic FunctionDocument27 pagesLogarithmic FunctionMary Joyce C. VillanuevaNo ratings yet
- 1.2 - Characteristics of Polynomial FunctionsDocument5 pages1.2 - Characteristics of Polynomial FunctionsPavni ChandaniNo ratings yet
- Inverse Functions: Teks Focus VocabularyDocument7 pagesInverse Functions: Teks Focus VocabularyAadarsh BalireddyNo ratings yet
- Protocolo IndividualDocument15 pagesProtocolo Individualoscar ortega mendozaNo ratings yet
- 7.4 Subchapter NotesDocument3 pages7.4 Subchapter NotesMe, Myself and INo ratings yet
- COLLEGE AND ADVANCE ALGEBRA Chapter 4Document31 pagesCOLLEGE AND ADVANCE ALGEBRA Chapter 4Myla VelascoNo ratings yet
- Characteristics of Rational FunctionsDocument27 pagesCharacteristics of Rational FunctionsGina VenturinaNo ratings yet
- CHAPTER 2 Revised Math Ed 101Document24 pagesCHAPTER 2 Revised Math Ed 101jinscollantesNo ratings yet
- Grade 7 Math Lesson 20: Polynomials Learning Guide: Term Is A Constant, A Variable or A Product of Constant and VariableDocument3 pagesGrade 7 Math Lesson 20: Polynomials Learning Guide: Term Is A Constant, A Variable or A Product of Constant and VariableKurt ManuelNo ratings yet
- 5.1 A S P P F: Ddition and Ubtraction of Olynomials and Olynomial UnctionsDocument11 pages5.1 A S P P F: Ddition and Ubtraction of Olynomials and Olynomial UnctionsJean Marie Ga LacsonNo ratings yet
- Finite Element Analysis-CharlesDocument91 pagesFinite Element Analysis-CharlesakshayaNo ratings yet
- Exponential Functions: More Mathematical ModelingDocument38 pagesExponential Functions: More Mathematical ModelingDaniel ClementeNo ratings yet
- 2017 Unit 3 Notes CH 6 CP A2Document47 pages2017 Unit 3 Notes CH 6 CP A2Ross HamiltonNo ratings yet
- Interpolation Part2Document122 pagesInterpolation Part2Thotakuri Sai Amith ChowdaryNo ratings yet
- Reviewer Simplifying RAEDocument8 pagesReviewer Simplifying RAEJashmine Mhae Mercado ArelladoNo ratings yet
- The Number Concept, True its Definition and The Division by ZeroFrom EverandThe Number Concept, True its Definition and The Division by ZeroNo ratings yet
- Reading StrategiesDocument10 pagesReading StrategiesAzizah IslamiyahNo ratings yet
- 1parts of SpeechDocument9 pages1parts of SpeechAzizah IslamiyahNo ratings yet
- 3.3 Division of Polynomials and The Remainder and Factor TheoremsDocument4 pages3.3 Division of Polynomials and The Remainder and Factor TheoremsAzizah IslamiyahNo ratings yet
- 4 9 Modeling With Polynomial FunctionsDocument5 pages4 9 Modeling With Polynomial FunctionsAzizah IslamiyahNo ratings yet
- MTM Lab (Metrology Part) - Spring 2021Document12 pagesMTM Lab (Metrology Part) - Spring 2021Rahul Raghunath BodankiNo ratings yet
- 2021 HhhhhhhterqasdwqwDocument1 page2021 HhhhhhhterqasdwqwHassan KhanNo ratings yet
- CHEMEXCILDocument28 pagesCHEMEXCILAmal JerryNo ratings yet
- Testbank ch01Document14 pagesTestbank ch01HườngNo ratings yet
- Chapter 10: Interrogative and Wh-Question ConstructionsDocument65 pagesChapter 10: Interrogative and Wh-Question ConstructionsHaithamNo ratings yet
- Lab Manual (Text)Document41 pagesLab Manual (Text)tuan nguyenNo ratings yet
- Santa Cruz Scanner FreqsDocument35 pagesSanta Cruz Scanner FreqsdonsterthemonsterNo ratings yet
- 5db83ef1f71e482 PDFDocument192 pages5db83ef1f71e482 PDFRajesh RoyNo ratings yet
- The Bishop ScoreDocument3 pagesThe Bishop ScoreJheanAlphonsineT.MeansNo ratings yet
- Safety AuditDocument25 pagesSafety AuditpoojaupesNo ratings yet
- St. John Adaptive Montessori School Magsaysay, Alicia, Isabela Monthly Exam in Science September Grade VI Name: - DateDocument3 pagesSt. John Adaptive Montessori School Magsaysay, Alicia, Isabela Monthly Exam in Science September Grade VI Name: - Date渡辺正平No ratings yet
- Department of Education: Republic of The PhilippinesDocument4 pagesDepartment of Education: Republic of The PhilippinesLOIDA AGUILARNo ratings yet
- Global Wine IndustryDocument134 pagesGlobal Wine IndustrySaifur Rahman Steve100% (2)
- Road Construction MethodsDocument163 pagesRoad Construction MethodsVetcher ColumnaNo ratings yet
- 3 PBDocument11 pages3 PBSuci DwiNo ratings yet
- PET-UT-U4 Without AnswersDocument2 pagesPET-UT-U4 Without AnswersAlejandroNo ratings yet
- Top 40 C Programming Interview Questions and AnswersDocument8 pagesTop 40 C Programming Interview Questions and Answersasanga_indrajithNo ratings yet
- Remanufactured Genuine Parts CatalogueDocument22 pagesRemanufactured Genuine Parts CatalogueHenrique CorreiaNo ratings yet
- COOKERY 9 Q3.Mod1Document5 pagesCOOKERY 9 Q3.Mod1Jessel Mejia Onza100% (4)
- Weebly Homework Article Review Standard 2Document11 pagesWeebly Homework Article Review Standard 2api-289106854No ratings yet
- Submarine Diesel EngineDocument106 pagesSubmarine Diesel EngineDharma Gita Surya PrayogaNo ratings yet
- Remembering and ForgettingDocument12 pagesRemembering and ForgettingChrstn BuenaventuraNo ratings yet
- Machining of Bezier Curve by Macro ProgrammingDocument7 pagesMachining of Bezier Curve by Macro ProgrammingAtul ChauhanNo ratings yet
- Tabel PeriodikDocument2 pagesTabel PeriodikNisrina KalyaNo ratings yet
- Vanishing Point by Felix Cheong SampleDocument13 pagesVanishing Point by Felix Cheong SampleWendy ChanNo ratings yet
- The Sabbath As FreedomDocument14 pagesThe Sabbath As Freedomapi-232715913No ratings yet