4⁄ 2 =2

RATIONAL FUNCTION AND F(-1) = 3(0) - 1 ⁄ 0 - 1

0 - 1 ⁄ -1
ITS GRAPH -1 ⁄ -1
1 ⁄ 1
Cartesian Plane example:
(divide both numbers to their
opposite sign)
REMEMBER: NO NEGATIVE
RESULTS

F(1) = 3(1) - 1 ⁄ 1 - 1
3-1⁄ 0
2 ⁄ 0 UNDEFINED
REMEMBER: DOMAIN SHOULD NOT
BE ZERO.

F(1) = 3(2) - 1 ⁄ 2 - 1
6-1⁄ 1
5 ⁄ 1 OR 5

POLYNOMIAL FUNCTION – where the

domain should not be zero.

Solving example:
Table of values:
X -2 -1 0 1 2

Y 7/3 2 1 0 5
OR or
F(X 2.3
)

GIVEN F(x)= 3x-1 ⁄ x-1

● Get the given function and
substitute the value of x.

If x = -2, therefore:
F(-2) = 3(-2)-1 ⁄ (-2) - 1
-6 - 1 ⁄ - 3
-7 ⁄ - 3 = 2.3

F(-1) = 3(-1)-1 ⁄ (-1) - 1

-3 - 1 ⁄ 2
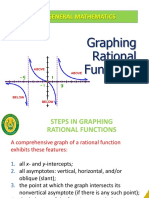
LESSON 1: INTERCEPS, ASYMPTOTES - an imaginary line to
which graph gets closer and closer as
ZEROES, AND the x or y increases or decreases its
ASYMPTOTES OF value without limit.
RATIONAL FUNCTIONS.
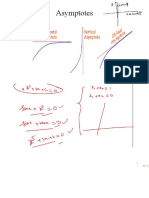
KINDS OF ASYMPTOTES
● Vertical asymptote
POLYNOMIAL FUNCTIONS
● Horizontal asymptote
- expressed as a quotient and can
● Oblique / slant
be written the form f(x)= p(x) ⁄
asymptote
q(x).
- q(x) is not a zero function or
VERTICAL ASYMPTOTES - to find this
should not be zero called
first reduce the given function to simplist
RATIONAL FUNCTIONS.
form then find the zeroes of the
denominator that are not zeroes of the
DOMAIN - set of first coordinates of a
numerator.
relation.
RANGE- set of first coordinates
HORIZONTAL ASYMPTOTE - to find
this, compare the degree of the
The points of intersection of its graph
numerator n and the degree of the
and an axis are the INTERCEPTS OF
denominator d.
THE GRAPH OF A RATIONAL
FUNCTION.
OBLIQUE / SLANT ASYMPTOTE - to
find this, divide the numerator by the
LET Y=0 to find the x intercept of a
denominator by either using long
function.
division or synthetic division. It is also
LET X=0 to find the y intercepts of a
the quotient with the remainder ignored
function.
and set equal to y.
The zeroes of the function is ALSO
SOLVING:
THE X - INTERCEPTS.
A. - DOMAIN - set of all numbers
B. - X INTERCEPT - let y = 0
INTERCEPTS - points of interaction of
C. - Y INTERCEPT - let x = 0
its graph and axis.
D. - ZEROES - same as x intercept
E. - VERTICAL ASYMPTOTE -
Y - INTERCEPT - to find y intercepts
restricted value for x
simply evaluate the function at x = 0.
F. - HORIZONTAL ASYMPTOTE -
(degree of
X - INTERCEPT - to find x intercept
numerator/denominator)
equate the function to zero.
dn < dd - Y = 0
dn = dd - Y = a/b
ZEROES OF A FUNCTION - are the
dn > dd - none
value of x which make the function zero.
GIVEN: FUNCTION IS DENOTED BY f. IT IS
f(x) = x² - x - 6 ⁄ x - 3 DEFINED BY THE EQUATION OF f(y) =
(x - 3) (x + 2) ⁄ x - 3 x IF AND ONLY IF f(x) = y FOR ANY y
IN RANGE B. SINCE BOTH ARE
A. DOMAIN FUNCTIONS, THEN A FUNCTION HAS
X - 3 = 0 (transpose 3 to the right) TO BE ONE-TO-ONE FOR ITS
X=3 INVERSE TO BE A FUNCTION AND AT
THE SAME TIME. IF IT IS A
{x|x∊R, except 3}
MANY-TO-ONE FUNCTION, ITS
INVERSE IS ONE-TO-MANY WHICH IS
B. X INTERCEPT NOT A FUNCTION.
Y = x² - x - 6 ⁄ x - 3 let y=0
0 = x² - x - 6 ⁄ x - 3 TO FIND THE INVERSE OF A
- multiply 0 to the denominator ONE-TO-ONE FUNCTION, CONSIDER
0 = f(x) = x² - x - 6 THE FOLLOWING:
(x - 3) (x + 2) A. EXPRESS THE FUNCTION IN THE
(x = 3) (x= -2) FORM OF y=f(x)
(3,0) (-2,0) B. INTERCHANGE THE x AND y
VARIABLE IN THE EQUATION
C. Y INTERCEPT C. SOLVE FOR y IN TERMS OF x.
Y = x² - x - 6 ⁄ x - 3
Y = 0² - 0 - 6 ⁄ 0 - 3
-6 ⁄ -3 = 2
(0,2)

D. ZEROES
X-2

E. VERTICAL ASYMPTOTE
X=3
FIND THE INVERSE FUNCTION OF
f(x)=3x-8
F. HORIZONTAL ASYMPTOTE - REPLACE X TO Y
NONE - INTERCHANGE THE VARIABLES
- TRANSPOSE
LESSON 2: INVERSE - DIVIDE BOTH SIDES BY 3 TO
ISOLATE THE Y
FUNCTION - FINAL ANSWER

INVERSE FUNCTION - IS A
FUNCTION WITH DOMAIN B AND
RANGE A GIVEN THAT THE
ORIGINAL FUNCTION IS DOMAIN A
AND RANGE B

THIS INVERSE FUNCTION OF

 JUST LIKE THE PREVIOUS PART WE
FIRST SOLVE FOR OUR INVERSE
FUNCTION

- REPLACE X TO Y
- INTERCHANGE THE VARIABLES - REPLACE X TO Y
- MULTIPLY Y-3 TO BOTH SIDES - INTERCHANGE THE VARIABLES
- DISTRIBUTE X - TRANSPOSE
- FACTOR OUT Y - DIVIDE BOTH SIDES BY 3 TO
- DIVIDE BOTH SIDES BY X-4 ISOLATE THE Y
- FINAL ANSWER - FINAL ANSWER

- SUBSTITUTE THE VALUE OF (X) TO

X
- MULTIPLY
- REPLACE X TO Y - ADD OR SUBTRACT
-INTERCHANGE THE VARIABLES - FINAL ANSWER
- TAKE THE CUBE ROOT TO BOTH - REPEAT THE SAME TO THE REST
SIDES
- CANCEL CUBE TO ISOLATE THE Y
- FINAL ANSWER

TABLE VALUES AND GRAPHS

 Exponential Function

Example:

Exponential Equations,
Exponential Inequalities and
Exponential Functions

Solving Exponential equation,

Exponential inequality and
Exponential functions

Steps for Solving Exponential

Equations
1.Determine if the numbers can be
written using the same base.

2.Rewrite the problem using the same

base.

3.Use one-to-one property of equality of

exponential functions, if the bases are
the same, then the exponents must be
equal. Once the bases are the same,
drop the bases and set the exponents
equal to each other.
4.Finish solving the problem by isolating
the variable.
4.Finish solving the problem by isolating
the variable.
Rules for Solving Inequalities
A. The direction of the inequality is
retained if:

i. The base 𝑏 of an inequality is greater

than 1.

ii. The same real number is added or

subtracted from both sides of an
inequality.

iii. Both sides of an inequality are

multiplied by or divided by the same
positive real number.

B. The direction of the

inequality is reversed if:
i. The base 𝑏 of an inequality is less
than 1.

ii. Both sides of an inequality are multiplied by

or divided by the same negative real number.

Steps for Solving Exponential

inequalities
1.Determine if the numbers can be
written using the same base.

2.Rewrite the problem using the same

base.

3.Use one-to-one property of equality of

exponential functions, if the bases are
the same, then the exponents must be
equal. Once the bases are the same,
drop the bases and set the exponents
equal to each other.