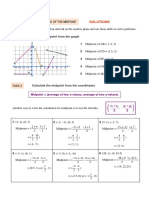
EXTENDING UNDERSTANDING OF THE MIDPOINT

Practise finding the midpoint of an interval. Then use this skill to solve problems.

TASK 1 Find the midpoint from the graph

Determine the coordinates of the midpoints of the intervals drawn on the graph.

1 Midpoint of AB = (−2, _____)

2 Midpoint of CD = ( _____ , _____ )

3 Midpoint of EF =

4 Midpoint of GH =

5 Midpoint of JK =

TASK 2 Calculate the midpoint from the coordinates

The pairs of coordinates are the end points of intervals.

Calculate the midpoint of each interval using:

Midpoint = (average of two x-values, average of two y-values)

1 (2, 3), (6, 7) 2 (−2, −1), (8, 3) 3 (5, 1), (−1, 7)

2+6 3+7 −2 + −1 + Midpoint =

Midpoint = ( , ) Midpoint = ( , )
2 2 2 2

8 10
=( , ) =( , )
2 2 2 2

= ( 4, ____ ) = ( ___ , ___ )

4 (−5, 1), (6, 1) 5 (−3, 8), (−2, –8) 6 (28, 1), (0, 43.5)

Midpoint = Midpoint = Midpoint =

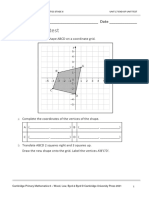
TASK 3 Determine the endpoint of an interval

Imagine M is the midpoint of an interval PQ.

P and M are shown on the diagram, but the other
end point, Q, is missing.
Determine the coordinates of Q using either the
diagram or the formula. Describe your method.

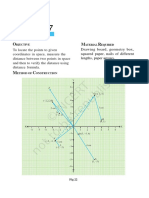
TASK 4 Use midpoints to investigate a relationship

AB and CD are parallel lines.

P and S are points on AB.
R and Q are points on CD.

1 Read off the midpoints of the two.

intervals.

Midpoint of PQ =

Midpoint of RS =

2 Mark the two midpoints on the graph and carefully draw the line through them. What do you notice
about your new line and the two lines AB and CD?

______________________________________________________________________________

______________________________________________________________________________

3 Draw in other intervals between the parallel lines. What do you notice about the midpoints of these
intervals?

______________________________________________________________________________

______________________________________________________________________________