Unit 6: Optimization

Lesson 6.1
The Critical Points and Extremum of a Function
Contents
Introduction 1

Learning Objectives 2

Warm Up 2

Learn about It! 4

Extrema of a Function 4
Critical Numbers 5
Absolute Extrema 8
Finding Absolute Extrema on a Closed Interval 9
Relative Extrema 10
First Derivative Test for Relative Extrema 11

Key Points 27

Check Your Understanding 29

Challenge Yourself 30

Bibliography 31

Key to Try It! 31

Unit 6: Optimization
Lesson 6.1

The Critical Points and Extremum

of a Function

Introduction
Have you ever wondered how engineers plan and estimate the cost of building a house
before they build it? They consider a lot of things, such as determining how many tiles should
be used, what materials they should use, or how many pipes they should use. Ultimately,
they should be able to maximize the use of their resources while keeping their costs to a
minimum.

6.1. The Critical Points and Extremum of a Function 1

Unit 6: Optimization
One of the useful applications of derivatives is optimization. In this method, we can
determine the minimum or maximum value in a situation, such as determining the
maximum volume of a box made from a sheet of cardboard or determining the minimum
costs of goods. This involves solving for the extrema of a function.

We can use the Extreme Value Theorem to identify the extrema of a function given the graph
of a function. In this lesson, we will discuss how to identify the extrema of a function given
its equation.

Learning Objectives
DepEd Competency
In this lesson, you should be able to do the
Solve optimization problems using
following:
critical points and extremum
● Determine the extrema of a function.
(STEM_BC11D-IIIg-1).
● Solve for the critical number(s) of a
function.
● Illustrate the relative and absolute
extrema of a function.

Warm Up
Lowest or Highest? 10 minutes
This activity will illustrate the maximum and minimum values.

Materials
● graphing paper
● pen

6.1. The Critical Points and Extremum of a Function 2

Unit 6: Optimization
Procedure
1. Graph the following quadratic functions on a rectangular coordinate system. Use the
table of values below as a format. The vertex is at (ℎ, 𝑘).

Data Table
Table 6.1.1. Table of values for 𝑓(𝑥) = 𝑥 2 + 2𝑥 − 1 and 𝑓(𝑥) = −𝑥 2 − 6𝑥 + 1
𝒙 ℎ−2 ℎ−1 ℎ ℎ+1 ℎ+2
𝒇(𝒙) 𝑘

a. 𝑓(𝑥) = 𝑥 2 + 2𝑥 − 1
b. 𝑓(𝑥) = −𝑥 2 − 6𝑥 + 1

2. Identify the vertex of each function and determine whether it is the highest or the
lowest point.
a. 𝑓(𝑥) = 𝑥 2 + 2𝑥 − 1
Vertex: ____________________
Highest or lowest point: ____________________

b. 𝑓(𝑥) = −𝑥 2 − 6𝑥 + 1
Vertex: ____________________
Highest or lowest point: ____________________

Guide Questions
1. Which function opens upward? downward?
2. Which function has a lowest point? highest point?
3. How can you determine if a quadratic function has a lowest point or a highest point
based on the equation?

6.1. The Critical Points and Extremum of a Function 3

Unit 6: Optimization

Learn about It!

In the Warm Up activity, you were able to locate the point where the extremum of a quadratic
function is located. The extremum of a quadratic function is at its vertex. Other functions have
extrema as well.

How do we determine the extrema of a function?

Extrema of a Function
The extrema (singular: extremum) of a function are the minimum and maximum points of a
function. The extrema of a function can be either relative or absolute, depending on the
interval and the function itself.
Let 𝑓 be a continuous function on an interval [𝑎, 𝑏] containing 𝑥0 .
1. 𝑓(𝑥0 ) is a minimum value of 𝑓 if 𝑓(𝑥0 ) ≤ 𝑓(𝑥) for all 𝑥 in [𝑎, 𝑏].
2. 𝑓(𝑥0 ) is a maximum value of 𝑓 if 𝑓(𝑥0 ) ≥ 𝑓(𝑥) for all 𝑥 in [𝑎, 𝑏].

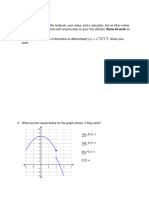
Consider Fig. 6.1.1.

Fig. 6.1.1. Graph of a continuous function on an interval [−2, 2]

6.1. The Critical Points and Extremum of a Function 4

Unit 6: Optimization
Based on the graph, we can observe that its lowest point is located at (𝟎. 𝟗, −𝟔. 𝟏). This means
that the function has a minimum of −𝟔. 𝟏 at 𝒙 = 𝟎. 𝟗. Similarly, its highest point is located at
(−𝟏. 𝟓, 𝟎. 𝟗). This means that the function has a maximum of 𝟎. 𝟗 at 𝒙 = −𝟏. 𝟓. These are the
extrema of the function at the given interval [−2, 2].

Critical Numbers
Let 𝑓 be a function defined at 𝑥0 . We say that 𝑥0 is a critical number if:
1. 𝑓 ′ (𝑥0 ) = 0, or
2. 𝑓 ′ (𝑥0 ) does not exist (𝑓 is not differentiable at 𝑥0 ).

The critical point of a function is shown in the following graphs.

Graph of the function 𝑓(𝑥) where 𝑓 ′ (𝑥0 ) = 0

6.1. The Critical Points and Extremum of a Function 5

Unit 6: Optimization

Graph of the function 𝑓(𝑥) where 𝑓′(𝑥0 ) does not exist

To find the critical numbers of the function 𝑓(𝑥), we can follow these steps:
1. Differentiate the function.
2. Find the value of 𝑥 where 𝑓 ′ (𝑥) = 0 or 𝑓′(𝑥) does not exist.

Example:
To find the critical numbers of the function 𝑓(𝑥) = 𝑥 2 − 2𝑥 + 1, we solve for its derivative.

𝑓(𝑥) = 𝑥 2 − 2𝑥 + 1
𝑓 ′ (𝑥) = 2𝑥 − 2

Since the derivative 𝑓′ is a polynomial, then it exists for any real number. Hence, to find the
critical numbers, equate 𝑓′ to zero.

2𝑥 − 2 = 0
2𝑥 = 2
𝑥=1

Thus, 𝒙 = 𝟏 is a critical number of the function 𝑓(𝑥) = 𝑥 2 − 2𝑥 + 1.

6.1. The Critical Points and Extremum of a Function 6

Unit 6: Optimization

What is/are the critical number(s) of

𝒈(𝒙) = 𝟑𝒙𝟐 − 𝟔𝒙 + 𝟖?

Remember
To find the critical numbers of a rational function, we equate both the
numerator and denominator of its derivative to zero.

𝑥2 𝑥 2−4𝑥
For example, the derivative of the function 𝑓(𝑥) = 𝑥−2 is 𝑓′(𝑥) = (𝑥−2)2 .

Let us solve the critical numbers of 𝑓(𝑥).

a. Equate the numerator to 0.

𝑥 2 − 4𝑥 = 0
𝑥(𝑥 − 4) = 0

𝑥 = 0, 𝑥 = 4

b. Equate the denominator to 0.

(𝑥 − 2)2 = 0
𝑥−2=0
𝑥=2

Since 𝑥 = 2 is not in the domain of 𝑓, the critical numbers of 𝑓 are

𝑥 = 0 and 𝑥 = 4.

6.1. The Critical Points and Extremum of a Function 7

Unit 6: Optimization
Absolute Extrema
The Extreme Value Theorem guarantees the existence of absolute (or global) extrema of a
function on a closed interval. Consider Fig. 6.1.2.

Fig. 6.1.2. Graph of a continuous function on an interval [−1.2, 2.5]

Notice that the lowest and highest points of the graph occur at the endpoints of the interval.
These endpoints serve as absolute extrema of the function. The function has an absolute
minimum of −1.4 at 𝑥 = −1.2 and an absolute maximum of 2.6 at 𝑥 = 2.5.

Let 𝑓 be a continuous function on a closed (or bounded) interval [𝑎, 𝑏] and 𝑥0 is in [𝑎, 𝑏].
1. 𝑓 has an absolute minimum at 𝑥0 if 𝑓(𝑥0 ) ≤ 𝑓(𝑥) for all 𝑥 in [𝑎, 𝑏].
2. 𝑓 has an absolute maximum at 𝑥0 if 𝑓(𝑥0 ) ≥ 𝑓(𝑥) for all 𝑥 in [𝑎, 𝑏].

Theorem 6.1.1
If 𝑓 is a continuous function on a closed interval [𝑎, 𝑏], then 𝑓 has absolute extrema, both
absolute minimum and absolute maximum, on this interval.

6.1. The Critical Points and Extremum of a Function 8

Unit 6: Optimization
Finding Absolute Extrema on a Closed Interval
Given an equation, the absolute extrema of a function 𝑓 (either minimum or maximum) on a
closed interval [𝑎, 𝑏] can be found by following these steps:
1. Determine the critical numbers of 𝑓.
2. Evaluate 𝑓 at the critical numbers and at the endpoints of [𝑎, 𝑏].
3. The least of these values is the absolute minimum of 𝑓, while the greatest of these
values is the absolute maximum of 𝑓.

A function can only have one absolute maximum and one absolute minimum on a closed
interval but may occur on at least one value of 𝒙. These extrema may occur at the critical
numbers or the endpoints of the interval.

Example:
The function 𝑓(𝑥) = 𝑥 2 − 2𝑥 + 1 has only one critical number, 𝑥 = 1. Evaluating 𝑓 at the critical
number 𝑥 = 1 and the endpoints of the interval [0, 3], we have the table of values below.

Table 6.1.2. Table of values for 𝑓(𝑥) = 𝑥 2 + 2𝑥 − 1

𝑥 0 𝟏 𝟑

𝑓(𝑥) 1 𝟎 𝟒

Based on the table, the function has an absolute minimum of 𝟎 at 𝒙 = 𝟏 and an absolute
maximum of 𝟒 at 𝒙 = 𝟑 on the interval [0, 3].

6.1. The Critical Points and Extremum of a Function 9

Unit 6: Optimization
Relative Extrema
Consider Fig. 6.1.3.

Fig. 6.1.3. Graph of a continuous function on an open interval (−1.2, 2.5)

Based on the graph, the relative (or local) extrema occur at the points (1.5, −0.6) and
(−0.2, 2.1). This means that the function has a relative minimum of −0.6 at 𝑥 = 1.5 and a
relative maximum of 2.1 at 𝑥 = −0.2.

Let 𝑓 be a continuous function and 𝑥0 , 𝑎, and 𝑏 are in the domain of 𝑓 such that 𝑎 < 𝑥0 < 𝑏.
1. 𝑓 has a relative minimum at 𝑥0 if there exists an open interval (𝑎, 𝑏) such that
𝑓(𝑥0 ) ≤ 𝑓(𝑥) for all 𝑥 in (𝑎, 𝑏).
2. 𝑓 has a relative maximum at 𝑥0 if there exists an open interval (𝑎, 𝑏) such that
𝑓(𝑥0 ) ≥ 𝑓(𝑥) for all 𝑥 in (𝑎, 𝑏).

Theorem 6.1.2
If 𝑓 has a relative extremum on an open interval at 𝑥0 , then 𝑥0 is a critical number of 𝑓.

Theorem 6.1.3
If 𝑓 has an absolute extremum on an open interval, then it occurs at the critical number of 𝑓.

6.1. The Critical Points and Extremum of a Function 10

Unit 6: Optimization
First Derivative Test for Relative Extrema
Suppose 𝑥0 is a critical number of a continuous function 𝑓.
1. If 𝑓′ changes from positive to negative at 𝑥0 , then 𝑓 has a relative maximum at 𝑥0 .
2. If 𝑓′ changes from negative to positive at 𝑥0 , then 𝑓 has a relative minimum at 𝑥0 .
3. Other ways that 𝑓 might have a relative extremum at 𝑥0 is if it is constant on one side
(or both sides) of 𝑥0 (that is, when 𝑓′ is zero on one or both sides of 𝑥0 ).
4. If 𝑓′ is both positive on both sides of 𝑥0 , or negative on both sides of 𝑥0 , then 𝑓 has no
relative extremum at 𝑥0 .

How can we determine if the extremum of a

function is maximum or minimum if we have an
open interval?

Let’s Practice!

Example 1
Determine the absolute extrema of the function 𝑓(𝑥) = 𝑥 2 − 8𝑥 + 12 on [−5, 3].

Solution
Step 1: Determine the critical number/s of the function.

Differentiate 𝑓(𝑥) = 𝑥 2 − 8𝑥 + 12.

𝑓(𝑥) = 𝑥 2 − 8𝑥 + 12
𝑓 ′ (𝑥) = 2𝑥 − 8

Equate 𝑓 ′ (𝑥) = 2𝑥 − 8 to zero and solve for 𝑥.

2𝑥 − 8 = 0
2𝑥 = 8
𝑥=4

6.1. The Critical Points and Extremum of a Function 11

Unit 6: Optimization
Thus, there is only one critical number, which is 𝑥 = 4.

Step 2: Evaluate 𝑓 at the critical number and the endpoints of [−5, 3].

Let us evaluate 𝑓 at 𝑥 = −5 and 𝑥 = 3. We will not be including 𝑥 = 4 since it is

not included in the interval [−5, 3].

𝑓(𝑥) = 𝑥 2 − 8𝑥 + 12

𝑓(−5) = (−5)2 − 8(−5) + 12

= 25 + 40 + 12
= 77
𝑓(3) = 32 − 8(3) + 12
= 9 − 24 + 12
= −3

𝑥 −𝟓 𝟑
𝑓(𝑥) 𝟕𝟕 −𝟑

Based on the table, the function has an absolute minimum of −𝟑 at 𝒙 = 𝟑 and an absolute
maximum of 𝟕𝟕 at 𝒙 = −𝟓.

1 Try It!
Determine the absolute extrema of the function 𝑓(𝑥) = −2𝑥 2 + 12𝑥 on [1, 4].

6.1. The Critical Points and Extremum of a Function 12

Unit 6: Optimization
Example 2
Find all relative extrema of the function 𝑓(𝑥) = 2𝑥 2 + 8𝑥 − 11.

Solution
Step 1: Determine the critical number/s of the function.

Differentiate 𝑓(𝑥) = 2𝑥 2 + 8𝑥 − 11.

𝑓(𝑥) = 2𝑥 2 + 8𝑥 − 11
𝑓 ′ (𝑥) = 4𝑥 + 8

Equate 𝑓 ′ (𝑥) = 4𝑥 + 8 to zero and solve for 𝑥.

4𝑥 + 8 = 0
4𝑥 = −8
𝑥 = −2

Step 2: Perform the first derivative test.

Since 𝑥 = −2 is the critical number, we will determine the signs of the values of
𝑓′(𝑥) at 𝑥 < −2 and 𝑥 > −2. In this case, let us use 𝑥 = −3 and 𝑥 = −1.

𝑓 ′ (𝑥) = 4𝑥 + 8
𝑓 ′ (−3) = 4(−3) + 8
= −12 + 8
= −4

This suggests that at 𝑥 < −2, 𝑓′(𝑥) is negative.

𝑓 ′ (𝑥) = 4𝑥 + 8
𝑓 ′ (−1) = 4(−1) + 8
= −4 + 8
=4

6.1. The Critical Points and Extremum of a Function 13

Unit 6: Optimization
This suggests that at 𝑥 > −2, 𝑓 ′ (𝑥) is positive.

Let us summarize the results using a table below.

𝒙 < −𝟐 𝒙 > −𝟐

𝑓 ′ (𝑥) − +

Based on the table, 𝑓′ changes from negative to positive at 𝑥 = −2. By the First
Derivative Test, 𝑓 has a relative minimum at 𝑥 = −2.

Step 3: Find the relative extrema.

To find the relative minimum, we evaluate the function at 𝑥 = −2.

𝑓(𝑥) = 2𝑥 2 + 8𝑥 − 11
𝑓(−2) = 2(−2)2 + 8(−2) − 11
= 2(4) − 16 − 11
= 8 − 16 − 11
= −19

Therefore, the function 𝑓(𝑥) = 2𝑥 2 + 8𝑥 − 11 has a relative minimum of −𝟏𝟗 at 𝒙 = −𝟐.

2 Try It!
Find all relative extrema of the function 𝑓(𝑥) = 2𝑥 2 + 8𝑥 − 11.

6.1. The Critical Points and Extremum of a Function 14

Unit 6: Optimization
Example 3
Find the absolute extrema of the function 𝑓(𝑥) = 𝑥 3 − 5𝑥 2 − 8𝑥 + 3 on the interval [−2, 5].

Solution
Step 1: Determine the critical number/s of the function.

Differentiate 𝑓(𝑥) = 𝑥 3 − 5𝑥 2 − 8𝑥 + 3.

𝑓(𝑥) = 𝑥 3 − 5𝑥 2 − 8𝑥 + 3
𝑓 ′ (𝑥) = 3𝑥 2 − 10𝑥 − 8

Equate 𝑓 ′ (𝑥) = 3𝑥 2 − 10𝑥 − 8 to zero and solve for 𝑥.

3𝑥 2 − 10𝑥 − 8 = 0
(3𝑥 + 2)(𝑥 − 4) = 0

3𝑥 + 2 = 0
2
𝑥=−
3
𝑥−4=0
𝑥=4

2
Thus, there are two critical numbers, which are 𝑥 = − 3 and 𝑥 = 4.

Step 2: Evaluate 𝑓 at the critical numbers and the endpoints of [−2, 5].

2
Let us determine the values of 𝑓(𝑥) at 𝑥 = −2, 𝑥 = − 3, 𝑥 = 4 and 𝑥 = 5.

𝑓(𝑥) = 𝑥 3 − 5𝑥 2 − 8𝑥 + 3

6.1. The Critical Points and Extremum of a Function 15

Unit 6: Optimization

𝑓(−2) = (−2)3 − 5(−2)2 − 8(−2) + 3

= −8 − 5(4) + 16 + 3
= −8 − 20 + 19
= −9

2 2 3 2 2 2
𝑓 (− ) = (− ) − 5 (− ) − 8 (− ) + 3
3 3 3 3
8 4 16
=− − 5( ) + +3
27 9 3
8 20 16
=− − + +3
27 9 3
157
=
27
≈ 5.815

𝑓(4) = 43 − 5(4)2 − 8(4) + 3

= 64 − 5(16) − 32 + 3
= 64 − 80 − 29
= −45

𝑓(5) = 53 − 5(5)2 − 8(5) + 3

= 125 − 5(25) − 40 + 3
= 125 − 125 − 37
= −37

𝟐
𝑥 −2 − 𝟒 5
𝟑
𝑓(𝑥) −9 𝟓. 𝟖𝟏𝟓 −𝟒𝟓 −37

Based on the table, the function has an absolute minimum of −𝟒𝟓 at 𝒙 = 𝟒 and an
𝟐
absolute maximum of 𝟓. 𝟖𝟏𝟓 at 𝒙 = − 𝟑.

6.1. The Critical Points and Extremum of a Function 16

Unit 6: Optimization

3 Try It!
Find the absolute extrema of the function 𝑓(𝑥) = 𝑥 3 − 6𝑥 2 + 12𝑥 − 1 on [−3, 1].

Example 4
2 3
Find the relative extrema of the function 𝑓(𝑥) = 3 𝑥 3 + 2 𝑥 2 − 2𝑥 + 9.

Solution
Step 1: Determine the critical number/s of the function.

2 3
Differentiate 𝑓(𝑥) = 3 𝑥 3 + 2 𝑥 2 − 2𝑥 + 9.

2 3 3 2
𝑓(𝑥) = 𝑥 + 𝑥 − 2𝑥 + 9
3 2
2
𝑓′(𝑥) = 2𝑥 + 3𝑥 − 2

Equate 𝑓 ′ (𝑥) = 2𝑥 2 + 3𝑥 − 2 to zero and solve for 𝑥.

2𝑥 2 + 3𝑥 − 2 = 0
(2𝑥 − 1)(𝑥 + 2) = 0

2𝑥 − 1 = 0
1
𝑥=
2

𝑥+2=0
𝑥 = −2

1
Thus, there are two critical numbers, which are 𝑥 = 2 and 𝑥 = −2.

6.1. The Critical Points and Extremum of a Function 17

Unit 6: Optimization
Step 2: Check the sign of 𝑓′ on both sides of the critical number.

1
The critical numbers 𝑥 = 2 and 𝑥 = −2 suggest that we can divide the number
1 1
line into three intervals: 𝑥 < −2, −2 < 𝑥 < 2, and 𝑥 > 2. Let us use some test

values to determine the sign of 𝑓′(𝑥) in the given intervals.

For 𝑥 < −2, let us use 𝑥 = −3.

𝑓 ′ (𝑥) = 2𝑥 2 + 3𝑥 − 2
𝑓 ′ (−3) = 2(−3)2 + 3(−3) − 2
= 2(9) − 9 − 2
= 18 − 9 − 2
=7

1
For −2 < 𝑥 < 2, let us use 𝑥 = 0.

𝑓 ′ (𝑥) = 2𝑥 2 + 3𝑥 − 2
𝑓 ′ (0) = 2(0)2 + 3(0) − 2
=0+0−2
= −2

1
For 𝑥 > 2, let us use 𝑥 = 1.

𝑓 ′ (𝑥) = 2𝑥 2 + 3𝑥 − 2
𝑓 ′ (1) = 2(1)2 + 3(1) − 2
=2+3−2
=3

6.1. The Critical Points and Extremum of a Function 18

Unit 6: Optimization
Note that we only have to observe the signs of the results of each value on the
given interval. Let us summarize the results using the table below.

𝟏 𝟏
𝒙 < −𝟐 −𝟐 < 𝒙 < 𝒙>
𝟐 𝟐

𝑓 ′ (𝑥) + − +

Based on the table, 𝑓′ changes from positive to negative at 𝑥 = −2, By the First
Derivative Test, 𝑓 has a relative maximum at 𝑥 = −2.

1
Similarly, 𝑓′ changes from negative to positive at 𝑥 = 2. This means that 𝑓 has a
1
relative minimum at 𝑥 = 2.

Step 3: Find the relative extrema.

1
To find the relative extrema, we evaluate the function at 𝑥 = −2 and at 𝑥 = 2.

2 3
𝑓(𝑥) = 𝑥 3 + 𝑥 2 − 2𝑥 + 9
3 2
2 3
𝑓(−2) = (−2)3 + (−2)2 − 2(−2) + 9
3 2
2 3
= (−8) + (4) + 4 + 9
3 2
16
= − + 6 + 13
3
41
=
3

6.1. The Critical Points and Extremum of a Function 19

Unit 6: Optimization
1 2 1 3 3 1 2 1
𝑓( ) = ( ) + ( ) − 2( )+ 9
2 3 2 2 2 2
2 1 3 1
= ( )+ ( )−1+9
3 8 2 4
1 3
= + +8
12 8
203
=
24

2 3 𝟒𝟏
Therefore, the function 𝑓(𝑥) = 3 𝑥 3 + 2 𝑥 2 − 2𝑥 + 9 has a relative maximum of at 𝒙 = −𝟐
𝟑
𝟐𝟎𝟑 𝟏
and a relative minimum of at 𝒙 = 𝟐.
𝟐𝟒

4 Try It!
1 5
Find the relative extrema of the function 𝑓(𝑥) = 3 𝑥 3 − 2 𝑥 2 − 6𝑥 − 2.

Tips
We can determine whether the absolute extremum of a polynomial
function is maximum or minimum by determining the behavior of its
graph.

1. Even functions have an absolute minimum if the leading

coefficient is positive, and an absolute maximum if the
leading coefficient is negative.
2. Odd functions have no absolute extremum.

Examples:
• The function 𝑓(𝑥) = 3𝑥 2 + 2 is an even function with a positive
leading coefficient. Thus, it has an absolute minimum.
• The function 𝑓(𝑥) = −𝑥 4 + 2𝑥 2 + 2 is an even function with a
negative leading coefficient. Thus, it has an absolute

6.1. The Critical Points and Extremum of a Function 20

Unit 6: Optimization
maximum.
• The function 𝑓(𝑥) = 𝑥 3 − 𝑥 is an odd function. Thus, it has no
absolute extremum although it has relative extrema.

Example 5
Find the absolute extrema of the function 𝑓(𝑥) = sin2 𝑥 + 2 cos 𝑥 on [0, 2𝜋].

Solution
Step 1: Determine the critical number/s of the function.

Differentiate 𝑓(𝑥) = sin2 𝑥 + 2 cos 𝑥.

𝑓(𝑥) = sin2 𝑥 + 2 cos 𝑥

𝑓(𝑥) = (sin 𝑥)(sin 𝑥) + 2 cos 𝑥
𝑑 𝑑 𝑑
𝑓 ′ (𝑥) = {sin 𝑥 (sin 𝑥) + [ (sin 𝑥)] sin 𝑥} + 2 ∙ (cos 𝑥)
𝑑𝑥 𝑑𝑥 𝑑𝑥
𝑓 ′ (𝑥) = [sin 𝑥 cos 𝑥 + cos 𝑥 sin 𝑥] + 2(− sin 𝑥)
𝑓 ′ (𝑥) = 2 sin 𝑥 cos 𝑥 − 2 sin 𝑥
𝑓 ′ (𝑥) = 2 sin 𝑥 (cos 𝑥 − 1)

Equate 𝑓 ′ (𝑥) = 2 sin 𝑥 (cos 𝑥 − 1) to zero and solve for 𝑥.

2 sin 𝑥 (cos 𝑥 − 1) = 0

2 sin 𝑥 = 0
sin 𝑥 = 0
𝑥 = 𝑛𝜋, 𝑛 ∈ ℤ

cos 𝑥 − 1 = 0
cos 𝑥 = 1
𝜋
𝑥 = + 𝑛𝜋, 𝑛 ∈ ℤ
2

6.1. The Critical Points and Extremum of a Function 21

Unit 6: Optimization
Given the interval [0, 2𝜋], we have the following critical numbers:

For 𝑥 = 𝑛𝜋, 𝑛 ∈ ℤ, we have 𝑥 = 0, 𝑥 = 𝜋, and 𝑥 = 2𝜋.

𝜋 𝜋 3𝜋
For 𝑥 = + 𝑛𝜋, 𝑛 ∈ ℤ, we have 𝑥 = and 𝑥 = .
2 2 2

Step 2: Evaluate 𝑓 at the critical numbers and the endpoints of [0, 2𝜋].

𝜋 3𝜋
Let us evaluate 𝑓(𝑥) at 𝑥 = 0, 𝑥 = 2 , 𝑥 = 𝜋, 𝑥 = and 𝑥 = 2𝜋.
2

𝑓(𝑥) = sin2 𝑥 + 2 cos 𝑥

𝑓(0) = sin2 0 + 2 cos 0

= 02 + 2(1)
=2

𝜋 𝜋 𝜋
𝑓 ( ) = sin2 + 2 cos
2 2 2
2
= (1) + 2(0)
=1

𝑓(𝜋) = sin2 𝜋 + 2 cos 𝜋

= 02 + 2(−1)
= −2

3𝜋 3𝜋 3𝜋
𝑓( ) = sin2 + 2 cos
2 2 2
2
= (−1) + 2(0)
=1

𝑓(2𝜋) = sin2 2𝜋 + 2 cos 2𝜋

= 02 + 2(1)
=2

6.1. The Critical Points and Extremum of a Function 22

Unit 6: Optimization

𝜋 3𝜋
𝑥 𝟎 𝝅 𝟐𝝅
2 2
𝑓(𝑥) 𝟐 1 −𝟐 1 𝟐

Based on the table, the function has an absolute minimum of −𝟐 at 𝒙 = 𝝅 and an

absolute maximum of 𝟐 at 𝒙 = 𝟎 and 𝒙 = 𝟐𝝅.

5 Try It!
1 1
Find the absolute extrema of the function 𝑓(𝑥) = − 2 𝑥 − 2 sin 𝑥 on [0, 2𝜋].

Example 6
What is the minimum sum of a positive number and its reciprocal?

Solution
Step 1: Express the sum 𝑓(𝑥) in terms of the number 𝑥.

1
Let 𝑥 be the number. Thus, its reciprocal is 𝑥. Hence, the sum is expressed as
1
𝑓(𝑥) = 𝑥 + 𝑥. Simplifying the function, we have

1
𝑓(𝑥) = 𝑥 +
𝑥
2
𝑥 +1
𝑓(𝑥) = .
𝑥

Step 2: Determine the critical number/s of the function.

𝑥 2+1
Differentiate 𝑓(𝑥) = .
𝑥

6.1. The Critical Points and Extremum of a Function 23

Unit 6: Optimization
𝑥2 + 1
𝑓 (𝑥) =
𝑥
𝒅 𝟐 𝒅
𝑥∙ (𝒙 + 𝟏) − (𝑥 2 + 1) ∙ 𝒙
′
𝑓 (𝑥) = 𝒅𝒙 𝒅𝒙
𝑥 2
2
𝑥(𝟐𝒙) − (𝑥 + 1)(𝟏)
𝑓 ′ (𝑥) =
𝑥2
2𝑥 2 − 𝑥 2 − 1
𝑓 ′ (𝑥) =
𝑥2
𝑥2 − 1
𝑓 ′ (𝑥) =
𝑥2

𝑥 2−1
Equate the numerator and denominator of 𝑓 ′ (𝑥) = to zero and solve for
𝑥2

𝑥.

𝑥2 − 1 = 0
𝑥2 = 1
𝑥 = ±1
𝑥 = 1 and 𝑥 = −1

𝑥2 = 0
𝑥=0

Step 3: Check the sign of 𝑓′ on both sides of the critical number.

The critical numbers 𝑥 = −1, 𝑥 = 0, and 𝑥 = 1 suggest that we can divide the
number line into four intervals: 𝑥 < −1, −1 < 𝑥 < 0, 0 < 𝑥 < 1, and 𝑥 > 1. Let
us use some test values to determine the sign of 𝑓′(𝑥) in the given intervals.

6.1. The Critical Points and Extremum of a Function 24

Unit 6: Optimization
For 𝑥 < −1, let us use 𝑥 = −2.

𝑥2 − 1
𝑓′(𝑥) =
𝑥2
(−2)2 − 1
𝑓′(−2) =
(−2)2
4−1
=
4
3
=
4

1
For −1 < 𝑥 < 0, let us use 𝑥 = − 2.

𝑥2 − 1
𝑓′(𝑥) =
𝑥2
1 2
1 (− 2) − 1
𝑓′ (− ) =
2 1 2
(− 2)
1
−1
=4
1
4
3
−4
=
1
4
= −3

1
For 0 < 𝑥 < 1, let us use 𝑥 = 2.

𝑥2 − 1
𝑓′(𝑥) =
𝑥2
1 2
1 (2) − 1
𝑓′ ( ) =
2 1 2
(2)
1
−1
=4
1
4

6.1. The Critical Points and Extremum of a Function 25

Unit 6: Optimization
3
−
= 4
1
4
= −3

For 𝑥 > 1, let us use 𝑥 = 2.

𝑥2 − 1
𝑓 ′ (𝑥) =
𝑥2
22 − 1
𝑓 ′ (2) =
22
4−1
=
4
3
=
4

𝒙 < −𝟏 −𝟏 < 𝒙 < 𝟎 𝟎<𝒙<𝟏 𝒙>𝟏

𝑓 ′ (𝑥) + − − +

Note that in the given problem, we are only dealing with positive numbers of
𝑥. Thus, we will be dealing with the interval [0, ∞).

Based on the table, 𝑓′ changes from negative to positive at 𝑥 = 1. By the First

Derivative Test, we have a relative minimum at 𝑥 = 1.

Step 4: Find the relative minimum.

𝑥2 + 1
𝑓(𝑥) =
𝑥
2
1 +1
𝑓(1) =
1
1+1
=
1
=2

6.1. The Critical Points and Extremum of a Function 26

Unit 6: Optimization
Therefore, the minimum sum that a positive number and its reciprocal can have is 2. This
happens when the number is 1.

6 Try It!
Find a positive number such that the sum of twice the number and the reciprocal of
twice the same number is a minimum.

Key Points
___________________________________________________________________________________________

● Let 𝑓 be a continuous function on an interval [𝑎, 𝑏] containing 𝑥0 .

○ 𝑓(𝑥0 ) is a minimum value of 𝑓 if 𝑓(𝑥0 ) ≤ 𝑓(𝑥) for all 𝑥 in [𝑎, 𝑏].
○ 𝑓(𝑥0 ) is a maximum value of 𝑓 if 𝑓(𝑥0 ) ≥ 𝑓(𝑥) for all 𝑥 in [𝑎, 𝑏].
● Let 𝑓 be a function defined at 𝑥0 . We say that 𝑥0 is a critical number if:
○ 𝑓 ′ (𝑥0 ) = 0, or
○ 𝑓 ′ (𝑥0 ) does not exist (𝑓 is not differentiable at 𝑥0 ).
● Let 𝑓 be a continuous function on a closed (or bounded) interval [𝑎, 𝑏] and 𝑥0 is in
[𝑎, 𝑏].
○ 𝑓 has an absolute minimum at 𝑥0 if 𝑓(𝑥0 ) ≤ 𝑓(𝑥) for all 𝑥 in [𝑎, 𝑏].
○ 𝑓 has an absolute maximum at 𝑥0 if 𝑓(𝑥0 ) ≥ 𝑓(𝑥) for all 𝑥 in [𝑎, 𝑏].
● If 𝑓 is a continuous function on a closed interval [𝑎, 𝑏], then 𝑓 has absolute extrema,
both absolute minimum and absolute maximum, on this interval.
● Given an equation, the absolute extrema of a function 𝑓 (either minimum or
maximum) on a closed interval [𝑎, 𝑏] can be easily found by following these steps:
○ Determine the critical numbers of 𝑓.
○ Evaluate 𝑓 at the critical number/s and at the endpoints of [𝑎, 𝑏].
○ The least of these values is the absolute minimum of 𝑓, while the greatest of
these values is the absolute maximum of 𝑓.

6.1. The Critical Points and Extremum of a Function 27

Unit 6: Optimization
● Let 𝑓 be a continuous function and 𝑥0 , 𝑎, and 𝑏 are in the domain of 𝑓 such that
𝑎 < 𝑥0 < 𝑏.
○ 𝑓 has a relative minimum at 𝑥0 if there exists an open interval (𝑎, 𝑏) such that
𝑓(𝑥0 ) ≤ 𝑓(𝑥) for all 𝑥 in (𝑎, 𝑏).
○ 𝑓 has a relative maximum at 𝑥0 if there exists an open interval (𝑎, 𝑏) such that
𝑓(𝑥0 ) ≥ 𝑓(𝑥) for all 𝑥 in (𝑎, 𝑏).
● If 𝑓 has a relative extremum on an open interval at 𝑥0 , then 𝑥0 is a critical number of
𝑓.
● If 𝑓 has an absolute extremum on an open interval, then it occurs at the critical
number of 𝑓.
● Suppose 𝑥0 is a critical number of a continuous function 𝑓. The First Derivative Test
for relative extrema states that:
○ If 𝑓′ changes from positive to negative at 𝑥0 , then 𝑓 has a relative maximum at
𝑥0 .
○ If 𝑓′ changes from negative to positive at 𝑥0 , then 𝑓 has a relative minimum at
𝑥0 .
○ Other ways that 𝑓 might have a relative extremum at 𝑥0 is if it is constant on
one side (or both sides) of 𝑥0 (that is, when 𝑓′ is zero on one or both sides of 𝑥0 )
○ If 𝑓′ is both positive on both sides of 𝑥0 , or negative on both sides of 𝑥0 , then 𝑓
has no local extremum at 𝑥0 .
___________________________________________________________________________________________

6.1. The Critical Points and Extremum of a Function 28

Unit 6: Optimization

Check Your Understanding

A. Determine all the critical numbers of the following functions.

1. 𝑓(𝑥) = 𝑥 2 − 4𝑥 + 1
2. 𝑓(𝑥) = |2𝑥 − 5| − 3
3. 𝑓(𝑥) = 𝑥 3 + 5𝑥 2 − 8𝑥 − 7
𝑥 2+5
4. 𝑓(𝑥) = 𝑥−1
𝑥 sin 𝑥
5. 𝑓(𝑥) = − 2 + +5
2

B. Determine the absolute extrema of the following functions and the

𝑥-values where the extrema occur on the given intervals.

1. 𝑓(𝑥) = 𝑥 2 + 2𝑥 − 3; [−2, 0]
2. 𝑓(𝑥) = 2𝑥 2 − 12𝑥 + 9; [1, 4]
3. 𝑓(𝑥) = 4𝑥 2 + 3𝑥 + 2; [−1, 0]
4. 𝑓(𝑥) = 𝑥 3 + 4𝑥 2 + 4𝑥 − 9; [−3, −1]
5. 𝑓(𝑥) = 2𝑥 3 + 6𝑥 2 − 18𝑥 + 5; [−5, 2]
4
6. 𝑓(𝑥) = 2𝑥 4 − 3 𝑥 3 − 16𝑥 2 + 16𝑥 + 1; [−3, 3]

7. 𝑓(𝑥) = − cos 𝑥 − 𝑥 + 2; [0, 𝜋]

8. 𝑓(𝑥) = sin 𝑥 + 1; [0, 𝜋]
9. 𝑓(𝑥) = −2 cos 𝑥 + 𝑥 + 3; [0, 2𝜋]
10. 𝑓(𝑥) = sin 𝑥 + cos 𝑥 ; [0, 2𝜋]
11. 𝑓(𝑥) = cos 𝑥 − sin 𝑥 − 4; [0, 2𝜋]
6
12. 𝑓(𝑥) = 𝑥 2−4 ; [−1, 1]

6.1. The Critical Points and Extremum of a Function 29

Unit 6: Optimization
C. Determine the extrema of the following functions and the 𝑥-values
where the extrema occur. Also, identify if it is relative or absolute.

1. 𝑓(𝑥) = 2𝑥 3 + 18𝑥 2 + 48𝑥 − 3

3 45 2
2. 𝑓(𝑥) = 4 𝑥 4 + 2𝑥 3 − 𝑥 +1
2
1 4 5 1 4
3. 𝑓(𝑥) = 3 𝑥 6 + 𝑥 − 2 𝑥4 − 3 𝑥3 +2
5

Challenge Yourself

Do as indicated.

1. Explain why 𝑓(𝑥) = 𝑥 3 has no extremum.

2. Give two quadratic functions 𝑓(𝑥) and 𝑔(𝑥) such that the absolute minimum of 𝑓(𝑥)
is 𝑥 = 2, and the absolute maximum of 𝑔(𝑥) is 𝑥 = 2.

3. Find a number such that the sum of the square of this number and the square of one
more than this number is a minimum.
4. A wire with a length of 20 meters is to be bent to form the largest possible rectangle.
What should be the dimensions of this rectangle?
5. An object is thrown vertically upward with an initial velocity of 64 feet per second. The
1
height ℎ feet of the object in 𝑡 seconds is given by the formula ℎ(𝑡) = 𝑣0 𝑡 − 2 𝑔𝑡 2 , where

𝑔 = 32 feet per second. At what time will the object reach its maximum height?

6.1. The Critical Points and Extremum of a Function 30

Unit 6: Optimization

Bibliography

Edwards, C.H., and David E. Penney. Calculus: Early Transcendentals. 7th ed. Upper Saddle
River, New Jersey: Pearson/Prentice Hall, 2008.

Larson, Ron H., and Bruce H. Edwards. Essential Calculus: Early Transcendental Functions.
Boston: Houghton Mifflin, 2008.

Leithold, Louis. The Calculus 7. New York: HarperCollins College Publ., 1997.

Smith, Robert T., and Roland B. Milton. Calculus. New York: McGraw Hill, 2012.

Tan, Soo T. Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach.
Australia: Brooks/Cole Cengage Learning, 2012.

Key to Try It!

1. absolute minimum of 10 at 𝑥 = 1, absolute maximum of 18 at 𝑥 = 3
2. minimum of −19 (relative and absolute) at 𝑥 = −2
3. absolute minimum of −118 at 𝑥 = −3, absolute maximum of 6 at 𝑥 = 1
7
4. relative minimum of −56 at 𝑥 = 6, relative maximum of 6 at 𝑥 = −1

5. absolute minimum of −𝜋 at 𝑥 = 2𝜋, absolute maximum of 0 at 𝑥 = 0

1
6. 2

6.1. The Critical Points and Extremum of a Function 31