4.

2 Preliminary Concepts
- Fourier Transform
• De nition: the Fourier transform of a continuous function
f (t) of a continuous variable t:

Euler’s formula
e jq = cos q + j sin q
Fourier transform pair
• inverse Fourier transform
¥
f (t ) = ò F ( µ )e j 2pµt
dµ
-¥
fi

 4.2 Preliminary Concepts

- Fourier Transform
• De nition: the Fourier transform of a continuous function
f (t) of a continuous variable t:

• Note: Fourier transform is an expansion of f(t) multiplied

by sinusoidal terms whose frequencies are determined by
the values of µ. Thus, because the only variable left after
integration is frequency, we say that the domain of the
Fourier transform is the frequency domain.
fi

 4.2 Preliminary Concepts

- Fourier Transform
• Example of the Fourier transform
f(t)

¥ W /2
F ( µ ) = ò f (t )e - j 2pµt
dt = ò Ae - j 2pµt dt
-¥ -W / 2

sin(pµW )
=
A
j 2pµ
e jpµW
[
-e - jpµW
= AW
(pµW )
] = AWsinc( μW )

sin(pm)
jq - jq sinc function: sinc(m) =
sin q = (e - e )/2 j (pm)

 4.2 Preliminary Concepts

- Fourier Transform
• Example of the Fourier transform
f(t)

¥ W /2
F ( µ ) = ò f (t )e - j 2pµt
dt = ò Ae - j 2pµt dt
-¥ -W / 2

sin(pµW )
=
A
j 2pµ
e [
jpµW
-e - jpµW
= AW ]
(pµW )
= AWsinc( μW )

sin q = (e jq - e - jq ) / 2 j
sinc function:

 4.2 Preliminary Concepts

- Fourier Transform
• Example of the Fourier transform

• Fourier transform:
width W

F ( µ ) = AWsinc( μW ) inversely proportional

contains complex terms

• Fourier spectrum:
Ch 3.2

for display purposes to

work with the magnitude

 4.2 Preliminary Concepts

- Fourier Transform
• Example of the Fourier transform of an impulse
f(t)
¥
F ( µ ) = ò f (t )e - j 2pµt
dt
-¥

¥
= ò d (t )e - j 2pµt dt = e - j 2pµ 0 = e 0 = 1
-¥

For impulse at t = t0
¥
F ( µ ) = ò d (t - t0 )e - j 2pµt
dt = e - j 2pµt 0
-¥

= cos(2pµt0 ) - j sin(2pµt0 )
a unit circle centered on the
origin of the complex plane

 4.2 Preliminary Concepts

- Fourier Transform
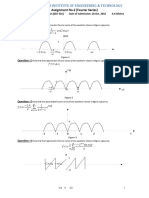
• Example of the Fourier transform of an impulse train
• Fourier transform pair:

¥ ¥
Á{F (t )} = ò F (t )e - j 2pµt
dt = ò F (t )e j 2p ( - µ ) t
dt = f (-u )
-¥ -¥

Á{d (t - t0 )} = e - j 2pµt 0

{ }
Á e - j 2pµt0 = d (- µ - t0 ) = d ((-t0 ) - µ ) = d (µ - (-t0 ) )

credit of this slide: Y. P. Hung

 4.2 Preliminary Concepts

- Fourier Transform
• Example of the Fourier transform of an impulse train
• Impulse train
¥
sDT (t ) = å d (t - nDT )
n = -¥

¥ 2pn ¥ 2pn 2pn

j t 1 1 j t DT / 2 -j t
åc e å ò
expressed as a
sDT (t ) = DT
= where ec = n
DT sDT (t )e DT
dt
Fourier series
n = -¥
n
DT n = -¥ DT - DT / 2

¥ 2pn ¥ 2pn
j t 1 j t
sDT (t ) = åc e
n = -¥
n
DT
=
DT
åe
n = -¥
DT

credit of this slide: Y. P. Hung

 4.2 Preliminary Concepts

- Fourier Transform
• Example of the Fourier transform of an impulse train

ìï 1 ¥ 2pn
ü 1 ìï ¥ j 2DpTn t ü
S ( µ ) = Á{sDT (t )} = Áí
j t

ïî DT
åe DT
ý= Áí å e ý
n = -¥ þ DT ïîn = -¥ þ
¥
1 æ n ö
=
DT
å dçµ -
n = -¥ è
÷
DT ø

Fourier transform of an impulse

¥

å d (t - nDT )
train is also an impulse train, but
with inverse proportional period sDT (t ) =
n = -¥