DEPARTAMENTO DE ENGENHARIA ELECTROTÉCNICA

3º TESTE DE ELECTRÓNICA III (2013/2014)

12 DE JUNHO DE 2013 – GRANDE AUDITÓRIO
14:00/15:15H
PROBLEM 1:
Consider a second order PLL with the block diagram depicted in Figure 1. The frequency of the
input frequency is 200 Mrad.s-1. Consider that the output frequency of the VCO as a function of the
( )
 285 + 1 − e − (vc − 4V ) × 100 if vc > 4 V

control voltage is given by: ωOUT ( vc ) = 5 + 80 × ( vc − 0.5) if 0.5V < vc ≤ 4V [Mrad/s]
 5 if vc ≤ 0.5 V

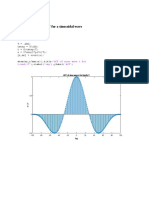
400
384.752
350

300

ωi Id(t) vc(t) v (t) 250

out
PD F(s) VCO ω.out v.c 200
vin(t) ωout ( ) 150

Figure 1: Block diagram of the PLL 100

50
5
0
0 1 2 3 4 5 6 7 8 9 10
0 v.c 10

Figure 2: VCO transfer function

a) Determine the linear model of the VCO for the input frequency value.
b) Considering that a XOR gate is used as phase detector, determine the linear model of the phase
detector, assuming that VDD=5V and that VSS=0V, justify your answer.
c) Considering that the loop filter (F(s)) has a pole and a zero, suggest a circuit that is capable of
implementing this transfer function, justify your answer by calculating the circuit transfer
function.
d) Calculate the closed loop transfer function of the PLL and calculate the values of the components
of the loop filter in order to obtain a closed loop bandwidth of 0.1 Mrad/s and a closed loop
system critically damped.
e) Determine the lock-in range of the PLL assuming that the input signal frequency changes slowly.
f) Draw the circuit of a 3-state phase-frequency detector with a charge pump current of 10 µA and
determine its linear model.
g) Considering that the loop filter (F(s)) has a pole and a zero, suggest a circuit that is capable of
implementing this transfer function using a charge pump, justify your answer by calculating the
circuit transfer function.
h) Explain why the static phase error of the PLL with this new phase detector is 0.
i) Calculate the closed loop transfer function of the PLL and calculate the values of the components
of the loop filter in order to obtain a closed loop bandwidth of 0.1 Mrad/s and a closed loop
system critically damped.
j) Explain how you would modify the PLL block diagram of figure 1 in order for the PLL to
produce an output frequency equal to 200 Mrad/s from an input frequency equal to 10 Mrad/s.
Calculate any new parameter value of the new block diagram.