LEARNING CONCEPTS AND ACTIVITIES

INVERSE OF A FUNCTION

We defined a function as a set of ordered pairs (𝑥, 𝑦) such that for every element 𝑥 in the domain,
there corresponds exactly one element 𝑦 in the range.

For example, the function 𝑓 relates the three sections 𝑥 and their class schedule 𝑦.
𝑓 = {(𝑇𝐿𝐸 𝑉𝑜𝑐, 1𝑝𝑚), (𝐻𝑈𝑀𝑆𝑆, 5𝑝𝑚), (𝑆𝑇𝐸𝑀 𝐴, 6𝑝𝑚)}

To find the inverse, interchange the elements in the domain with the elements in the range. Hence,
the inverse of the given function is given by
{(1𝑝𝑚, 𝑇𝐿𝐸 𝑉𝑜𝑐), (5𝑝𝑚, 𝐻𝑈𝑀𝑆𝑆), (6𝑝𝑚, 𝑆𝑇𝐸𝑀 𝐴)}

Inverse of a Function
If the function 𝑓 is a set of ordered pairs (𝑥, 𝑦), then the inverse of 𝑓 is the set
of ordered pairs (𝑦, 𝑥).

Example: Find the inverse of the following functions.

1. {(−1,1), (0,0), (1,1)} 2. {(−2, 2), (−1, 3), (0, 4), (1, 5), (2, 6)}
Answer: Answer:
The inverse of the given function is found The inverse of the given function is
by interchanging the entries in each {(𝟐, −𝟐), (𝟑, −𝟏), (𝟒, 𝟎), (𝟓, 𝟏), (𝟔, 𝟐)}
ordered pair.
{(𝟏, −𝟏), (𝟎, 𝟎), (𝟏, 𝟏)}

ONE-TO-ONE FUNCTION
A function is called one-to-one function if no elements of (A) have the same image in elements of
(B).
Australia = AU
Philippines = PH
Singapore = SG
United States = US
Hongkong = HK

There is a unique Learner’s Number Each country has a unique

assigned to every student and it country code then. Each unique
cannot be given to another. It is an code is assigned to only one
example of one-to-one function. country. Therefore, it is a one-to-
one function.

Consider the given functions below. The arrow diagram shows an example and non-example of
one-to-one function.
One-to-one function Not One-to-one function

GENERAL MATHEMATICS Page | 1

 The element in B correspond to
only one value in set A.
Therefore, it is a one-to-one
function.
The element in B correspond to two values in A.
{(𝟏, 𝟒), (𝟐, 𝟔), (𝟑, 𝟖), (𝟒, 𝟖)}
The range element 8 has two different x-coordinates,
3 and 4. Interchanging the 𝑥-value and 𝑦-value
produces a relation that violates the definition of a
function.
{(𝟒, 𝟏), (𝟔, 𝟐), (𝟖, 𝟑), (𝟖, 𝟒)}
Hence, it is not one-to-one function.

Ways to Determine if a Function is One-to-One

• Algebra Manipulation
If you substitute both positive and negative of a number to function and gives a unique
answer, then it is one-to-one.

𝟏. 𝒇(𝒙) = 𝟐𝒙 𝟐. 𝒇(𝒙) = 𝒙𝟐 − 𝟏 𝟑. 𝒇(𝒙) = 𝟐𝒙𝟑 𝟒. 𝒇(𝒙) = |𝒙|

𝑓(1) = 2(1) = 2 𝑓(2) = (2)2 − 1 = 3 𝑓(3) = 2(3)3 = 2(27) 𝑓(10) = |10| = 10

𝑓(−1) = 2(−1) = −2 𝑓(−2) = (−2)2 − 1 = 54 𝑓(−10) = |−10| = 10
=3 𝑓(−3) = 2(−3)3
It is one-to-one = 2(−27) = −54 It is not one-to-one.
function because it It is not one-to-one.
gives different It is one-to-one
elements in the function.
range.

• Horizontal Line Test

It is a test used to determine if a function is one-to-one. If a horizontal line intersects a
function’s graph more than once, then the function is not one-to-one.

Restricting the Domain

Inverse of a Function
• The inverse of the function 𝑓 is often denoted by 𝑓 −1 . The notation 𝑓 −1 for an inverse function
1 1
does not mean . The function denoted by is called reciprocal function and is an entirely
𝑓 𝑓
different function from 𝑓 −1 .
• A function 𝑓 has an inverse function if and only if it is a one-to-one function.

To find the inverse 𝑓 −1 of the one-to-one function 𝑓:

1. Substitute 𝑦 for 𝑓(𝑥).
2. Interchange 𝑥 and 𝑦.
3. Solve, if possible, for 𝑦 in terms of 𝑥.
4. Substitute 𝑓 −1 (𝑥) for 𝑦.
5. Verify that the domain of 𝑓 is the range of 𝑓 −1 and that the range of 𝑓 is the domain of 𝑓 −1 .

GENERAL MATHEMATICS Page | 2

Examples:
Find the inverse of the following functions.
1. 𝑓(𝑥) = 4𝑥 + 6
3𝑥
2. 𝑔(𝑥) =
𝑥+2
𝑥+1
3. ℎ(𝑥) =
3
4. 𝑖(𝑥) = 𝑥3 −
2
5. 𝑗(𝑥) = 𝑥 + 4𝑥 − 2
2

𝑓(𝑥) = 4𝑥 + 6 3𝑥 𝑥+1 𝑖(𝑥) = 𝑥 3 − 2 𝑗(𝑥) = 𝑥 2 + 4𝑥 − 2

𝑔(𝑥) = ℎ(𝑥) =
𝑥+2 3
Begin by 𝑦 = 𝑥3 − 2 This is a quadratic
substituting 𝑦 for Replace g(x) with 𝑥+1 𝑥 = 𝑦3 − 2 function with a
𝑦=
𝑓(𝑥). y. 3 𝑦3 = 𝑥 + 2 graph in the
3𝑥 𝑦+1
shape of a
3
𝑦 = 4𝑥 + 6 𝑥= 𝑦 = √𝑥 + 2
𝑦= 3
Interchanging 𝑥 𝑥+2 parabola that
Interchange x 3𝑥 = 𝑦 + 1
and 𝑦 yields 3
𝑖 −1 = √𝑥 + 2 open upward.
and y. 𝑦 = 3𝑥 − 1
𝑥 = 4𝑦 + 6
Solve for 𝑦. 3𝑦
𝑥= It is not one-to-
𝑦+2 ℎ−1 (𝑥) = 3𝑥 − 1
4𝑦 = 𝑥 − 6 one function as it
𝑥−6 Solve for 𝑦. fails the
𝑦= 𝑥(𝑦 + 2) = 3𝑦
4 HORIZONTAL TEST.
The inverse 𝑥𝑦 + 2𝑥 = 3𝑦
notation, 2𝑥 = 3𝑦 − 𝑥𝑦 Therefore, the
𝒙−𝟔 2𝑥 = 𝑦(𝑥 − 3)
𝒇−𝟏 (𝒙) = function 𝑗(𝑥) has
𝟒 2𝑥
=𝑦 no inverse.
𝑥−3
2𝑥
𝑦=
𝑥−3
−1
2𝑥
𝑔 (𝑥) =
𝑥−3

• A relation reversing the process performed by any function 𝑓(𝑥) is called the inverse of 𝑓(𝑥).
This means that the domain of the inverse is the range of the original function and that
range of the inverse is the domain of the original function.

If 𝑓 is a one-to-one function with domain 𝑋 and range 𝑌, and 𝑔 is a function

with domain 𝑌 and range 𝑋, then 𝑔 is the inverse function of 𝑓 if and only 𝑖𝑓
𝒇[𝒈(𝒙)] = 𝒙 , for all 𝑥 in the domain of 𝑔 and
𝒈[𝒇(𝒙)] = 𝒙 , for all 𝑥 in the domain of 𝑓.

Example:
Determine whether the functions below are inverses of each other or not.
1 𝑥+2 𝑥
1. 𝑓(𝑥) = − 𝑥 and g(𝑥) = −2𝑥 2. 𝑓(𝑥) = 4𝑥 − 2 and g(𝑥) = 3. 𝑓(𝑥) = 3𝑥 + 1 and 𝑔(𝑥) =
2 4 3

𝑓[𝑔(𝑥)] = 𝑓(−2𝑥) 𝑥+2 𝑥

𝑓[𝑔(𝑥)] = 𝑓 ( ) 𝑓[𝑔(𝑥)] = 𝑓 ( )
1 4 3
= − (−2𝑥) 𝑥
2 𝑥+2 = 3( )+1
=𝑥 = 4( )−2 3
4 =𝑥+1
=𝑥+2−2
1 =𝑥
𝑔[𝑓(𝑥)] = 𝑔 (− 𝑥) 𝑔[𝑓(𝑥)] = 𝑔(3𝑥 + 1)
2 3𝑥 + 1
1 𝑔[𝑓(𝑥)] = 𝑔(4𝑥 − 2) =
= −2𝑥 (− 𝑥) (4𝑥 − 2) + 2 3
2 1
=𝑥 = =𝑥+
4 3
4𝑥
=
Therefore, by definition, the two 4 𝑓[𝑔(𝑥)] ≠ 𝑔[𝑓(𝑥)] ≠ 𝑥
functions are inverses of each =𝑥
Thus, the functions are not
other. inverses of each other.
𝑓[𝑔(𝑥)] = 𝑔[𝑓(𝑥)] = 𝑥

GENERAL MATHEMATICS Page | 3

 The functions 𝑓 and 𝑔 are
inverses of each other.

APPLICATION OF INVERSE FUNCTION

GRAPH OF THE INVERSE FUNCTION

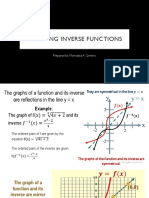
The graph of a function 𝑓 and the graph of the inverse function 𝑓 −1 are symmetric
with respect to the line given by 𝑦 = 𝑥.

Sketch the graph of 𝑔(𝑥) = 𝑥 2 at 𝑥 ≥ 0. The graph below is a one-to-one function 𝒚 =

𝒇(𝒙). Draw the graph of its inverse.
x 0 1 2 3 4
y 0 1 4 9 16

x -5 -2 4
y 6 2 -3

Since the points (–5, 6), (– 2, 2), and (4, –3) are
The line 𝑦 = 𝑥 is not part of the graph of 𝑔 or its on the graph of 𝑓, then the points (6, –5), (2, –
inverse 𝑔−1 . It is included to illustrate that the 2), and (–3, 4) are on the graph of 𝑓 −1 .
graph of 𝑔 and 𝑔−1 are symmetric with respect
to the line 𝑦 = 𝑥. Inverse Function
x 6 2 -3
y -5 -2 4

GENERAL MATHEMATICS Page | 4