Industrial

Fans and Blowers Plant Design

mechanism, support for a belt drive or a direct connection.

Centrifugal fans are those in which the flow of air changes
its direction, in an angle of 90°, between the entrance and
exit.
Fans and Blowers Drawings
A fan is a rotodynamic device and is the driving part
Propeller Fan – wheel usually
of all ventilating systems. The energy of rotation applied to
have two or more single thickness
the fan shaft is converted into pressure difference, causing
blades in a single ring enclosure.
the air, gas, or particulate matter to flow through the duct-
Efficiencies are generally low and use
work or discharge into a free space.
is limited to low pressure. Applica-
tion – High volume air moving
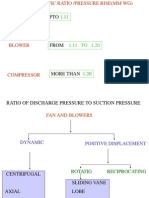
To be classed as a fan, the work per unit mass on
application such as air circulation
the gas must be less than 25 kJ/kg; above this value it is
within a space or ventilation through a wall without attached
called a turbo compressor. Hence, the fan pressure must not
duct work.
exceed the standard air density of 1.2 kg/m3 x 25 kJ/kg,
giving 30 kPa (~3000 mmwg) with the pressure ratio not
Tube axial – the wheel is
exceeding 1.30, taking atmospheric pressure as 100 kPa.
similar to the propeller type except
Note: air's density at 101325 Pa, 21.111°C (70°F) is
it usually has more blades of a
1.200058.
heavier thickness to increase
efficiency and pressure capability.
Category According to Work per Unit Mass
Application – Ducted HVAC
application where air distribution
Descrip- Work per unit Maximum fan
on the downstream side is not critical. Industrial applications
tion mass, kJ/kg pressure, kPa Class
include drying ovens, paint spray booths and fume exhaust
systems.
Low 0 – 0.6 0 – 0.7 1
Pressure 0.6 – 0.833 0.7 – 1.0 2
Vane axial – The most
0.833 – 1.333 1.0 – 1.6 3
efficient axial type fan. It uses
1.333 – 1.667 1.6 – 2.0 4
straightening vanes to improve
High 1.667 – 3.00 3.0 – 3.6
efficiency and pressure capa-
bility. Blades often have airfoil
shapes and may be available with
A blower is a fan used to force air under pressure.
adjustable pitch. Pressure capabilities are medium to high.
That is, the resistance to gas flow is imposed primarily upon
Application – General HVAC systems especially where
the outlet.
straight through flow and compactness is required. Good
down-stream air distribution. Used in many industrial
An exhauster is a fan used to withdraw air under
applications.
suction. That is, the resistance to gas flow is imposed
primarily upon the inlet
Inline Centrifugal – This type
is actually a centrifugal fan with an
Fans are workhorses of exhaust ventilation system.
airfoil or backward inclined wheel in
They must be the appropriate size and type to make the
a vane axial casing. Good efficiency
ventilation system work effectively. They must provide
but with lower pressure than a
enough air pressure difference (“suction”) to capture
similar type centrifugal fan.
contaminants at the source, draw them through the hood,
Application – Used primarily for low pressure return air
carry them through the ducting and exhaust them outdoors.
systems in HVAC applications. Has straight through flow.
There are two main types of exhaust fans – axial
Forward Curved – The
fans and centrifugal fans. Axial fans, usually resembling
wheel’s blades are small and
propellers, draw air straight through the fan. Centrifugal
curved forward in the direction of
fans, resembling squirrel cages, draw air into the center of
the wheel’s rotation. This fan runs
the fan and exhaust it at a 90-degree angle.
at a relatively low speed to move a
given amount of air. This wheel
Axial or propeller fans are most commonly used
type is most often called a squirrel
for dilution ventilation or for cooling. These fans are often
cage wheel. Application – Primarily for low pressure HVAC
mounted in a wall or ceiling. They can move large amounts
such as domestic furnaces, central station units and
of air if there is little resistance, but are not suited for local
packaged air conditioning equipment.
exhaust ventilation because they do not provide enough
suction to withdraw air through the system.
Radial blade – This wheel is
like a paddle wheel with or without
Centrifugal fans can operate against a high
side rims. The blades are
resistance and are typically used in local exhaust ventilation
perpendicular to the direction of
systems. There are several types of centrifugal fans. The
the wheel’s rotation and the fan
rugged radial blade centrifugal fans are the best type for
runs at a relatively medium speed
exhausting heavy amounts of dust because they are less
to move a given amount of air.
likely to become clogged or abraded by the dust.
Application – the radial blade type is designed for material
handling applications. It features rugged construction and
Types of Fans simple field repair. It is also used for high-pressure industrial
requirements.
Propeller fan – consists of a propeller or disk type
wheel within a mounting ring or plate and includes a driving Backward inclined – the
mechanism, support for a belt drive or a direct connection. wheel blades are flat and lean
away from the direction of the
Tube axial fan – consists of a propeller or disk wheel’s rotation. This fan runs at a
type within a cylinder and includes a driving mechanism, relatively high speed to move a
support for a belt drive or a direct connection. given amount of air. It is more
efficient that the above listed
Centrifugal fan – consists of a fan rotor or rotor types. Application – general HVAC systems. Used in many
wheel within a scroll type of housing and includes a driving industrial applications where the airfoil blade might be

1 Patrick D. Sta. Maria / February 26, 2023

 Industrial
Fans and Blowers Plant Design

subjected to erosion from light dust. The capacity of the fan is the volume flow rate of
the fan outlet.
Airfoil blade – Although not a
“basic type”, this is an important Q = AV
refinement of the backward
inclined wheel design. It has the The power output of a fan or air power is based
highest efficiency and runs at a on fan volume and the fan total pressure.
slightly higher speed than the
standard flat blade to move a given PAIR = QWAIRhAIR
amount of air. Applications – Most efficient of all
centrifugals, this is usually used in both large HVAC system Q – fan capacity, m3/s
and clean air industrial applications where the energy W – specific weight of air
savings are significant. Can be made with special – 11.772 N/m3 at 21.11°C
construction for dusty air. h – total head, m of air

Radial Tip – The wheel’s Fan heads are usually given in centimeters of water
blades are somewhat cupped in (cmwg), that is, head in terms of water. To calculate the fan
the direction of the wheel’s power required using Qwh, the head given needs to be con-
rotation but the blades leans back verted to meters of air using the densities of both fluids.
so that its outside tip approaches a
radial position. This fan runs at P = hWwW = hAwA
approximately the same speed as
a backward inclined wheel to move a given amount of air. hA = (9810 N/m3)(hW)
Applications – This type is also designed for material 11.772 N/m3 hA = 833.33 hW
handling or dirty or erosive applications and is more efficient
that the radial blade type.
This means that for air at 21.11°C to exert the same
pressure as 1 m of water, the column of air needs to be
Performance of Fans 833.33 m high. Power is then calculated by the formula
given above.
Fan performance is a statement of volume, total
pressures, static pressures, speed, power input, mechanical Since pressure is the product of the specific weight
and static efficiency at standard air density. of the fluid and the height of its column, power may also be
calculated if the wh part of the equation is replaced by pres-
Static Head is the height of the surface of a fluid sure in N/m2 or Pa.
above the gauge point.
hS = ρW hW P = (m3/s)(N/m2) = N-m/s = W
ρA
In English units, the pressure is usually given in
hS – static head, m of air inches of water and the horsepower requirement is calcu-
hW – manometer reading, m of water lated using the same formula, P = Qwh, where both w and h
ρW – density of water, 1000 kg/m3 pertains to the same fluid.
– 9810 N/m3
ρA – density of air, 1.2 kg/m3 At 70°F (21.11°C) air has a density of
– 11.772 N/m3 at 21.11°C (70°F)
m = (14.69595 lb/in2)(144 in2/ft2)
(53.34 ft-lb/lb-°R)(70 + 459.67°R)
11.772N/m3 = (1.2kg/m3)(9.81 N/kg) m = 0.0749 lb/ft3
1.2kg/m3 = density of air at 21.11°C 101.3 kPa
Densities of 62.4 lb/ft3 for water and 0.075 lb/ft3 for
Static pressure is air pressure caused by its air will be used. Power is then P = Qwh/550 where:
degree of compression. It can be positive or negative. In the
fan, it is equivalent to the difference between the static Q – discharge, ft3/s
outlet pressure and the total inlet pressure. w – specific weight, lb/ft3
h – height, ft
Velocity Head is the head required to produce the 550 – conversion factor from ft-lb/s to horsepower
flow of fluid.

The power input of a fan or its brake power is

hV = V2 / 2g g = 9.81 m/s2, 32.174 ft/s2
the power delivered to the fan shaft.
Dynamic pressure is air pressure caused by move-
ment. Dynamic pressure can only be positive. In the fan, it is PBRAKE = PAIR / eM
equivalent to the average of the speeds at the outlets.
eM – mechanical efficiency of the fan
Total head is the sum of the static head and the
velocity head. The static efficiency of the fan is the mechanical
efficiency multiplied by the ratio of the static pressure to the
h = hS + hV
total pressure.
eS = eM (hS / h)
notes: in fan design there is no elevation head because
fans are

Total pressure is air pressure owing to compres-

Fan Laws
sion and movement. It is the algebraic sum of the dynamic
and static pressures at a certain point. Therefore, if the air is There are three basic fan laws which encompass all
motionless the total pressure equals the static pressure. In fan functional principles.
the fan, it is the difference between the total pressures
determined at its inlet and outlet. 1. Fan Speed Variation (constant fan size, constant
density)
Q2 = N2 H2 = N2 2 P2 = N2 3
Capacity of Fan Q1 N1 H1 N1 P1 N1

2 Patrick D. Sta. Maria / February 26, 2023

 Industrial
Fans and Blowers Plant Design

2. Fan Size Variation (constant speed, constant gymnasiums 2 – 10

density) kitchens, hospitals 2–5
Q2 = D2 H2 = D2 2 P2 = D2 3 kitchens, resident 2–5
Q1 D1 H1 D1 P1 D1 kitchens, restaurant 1–3
laboratories 1–5
3. Gas Density Variation (constant speed, constant laundries 1–3
fan size) markets 2 – 10
offices 2 – 10
Q2 = Q1 H2 = ρ2 P2 = ρ2 3 packing houses 2–5
H1 ρ1 P1 ρ1 plating rooms 1–5
pool rooms 2–5
projection rooms 1–3
Bernoulli’s Equation Applied to Fans recreation rooms 2 – 10
residences 2–5
Total Head = Static Pressure Head + Velocity Head
sales rooms 2 – 10
+ Head Loss
theaters 2–8
toilets 2–5
h = PD – PS + VD – VS + hL transformer rooms 1–5
wA 2g warehouses 2 – 10

h – total head, m
P – pressure, Pa Allowable Velocities In Fan systems
wA – specific weight of air, N/m3 (feet per minute)
V – velocity, m/s KENT’s Power Volume / 12–50
D – discharge
S – suction Location
Residences School and Industrial
Note : The head may be computed or expressed Public Buildings Buildings
either in terms of meters of water or meters of air. Use outside air intake
proper material for the specific weight, i.e., water or air. 700 - 800 800 – 900 1000 – 1200
filters
250 – 300 300 – 350 350
Density of Water (°C – kg/m3) air washers
500 500 500
11999.6002 31995.4211 fan suction connection
12999.5002 32995.0249 700 - 900 800 – 1000 1000 – 1400
13999.3005 33994.7279 fan outlets
14999.2006 34994.4312 1000 – 1700 1300 – 2200 1600 – 2800
15999.1008 35994.0358 main ducts
16998.9012 36993.7394 700 - 1000 1000 – 1400 1200 – 2000
17998.8014 37993.3446 branch ducts
18998.6020 38992.9501 600 - 700 600 – 1000 800 – 1200
19998.4026 39992.6544 branch risers
20998.2032 40992.2604 500 - 650 600 – 900 800 – 1000
21998.0040 41991.8667 ceiling registers
22997.8048 42991.4733 400 - 500 500 – 1400 800 – 2000
23997.6057 43991.0803 return grilles
24997.3073 44990.5894 350 - 500 500 – 1000 800 – 1500
25997.1084 45990.1970
26996.8102 46989.8050 Multiply by 0.00508 to convert to m/s.
27996.5122 47989.3154
28996.3136 48988.9241
29996.0159 49988.4353
30995.7184 50988.0447
Fan Calculations
Average Air Changes Required Per
Minute for Good Ventilation A fan is a rotodynamic device and is the driving part
of all mechanical ventilating systems. The energy of rotation
minutes per change applied to the fan shaft is converted into pressure
assembly hall 2 – 10 difference, causing the air, gas, or particulate matter to flow
auditoriums 2 – 10 through the ductwork or discharge into a free space.
bakeries 2–3
banks 3 – 10 To be classed as a fan, the work per unit mass on
barns 10 – 20 the gas must be less than 25 kJ/kg; above this value it is
bars 2–5 called a turbo compressor. Hence, the fan pressure must not
beauty parlors 2–5 exceed the standard air density of 1.2 kg/m3 x 25 kJ/kg,
boiler rooms 1–5 giving 30 kPa (~3000 mmwg) with the pressure ratio not
bowling alleys 2 – 10 exceeding 1.30, taking the atmospheric pressure as 100 kPa.
churches 5 – 10 (Industrial Ventilation Handbook p. 742)
clubs 2 – 10
dairies 2–5
dance halls 2 – 10
dining rooms 3 – 10
dry cleaners 1–5
engine rooms 1–3
factories 2–5
forge shops 2–5
foundries 1–5
garages 2 – 10
generator rooms 2–5

3 Patrick D. Sta. Maria / February 26, 2023

 Industrial
Fans and Blowers Plant Design

w = (1.18 kg/m3)(9.81 kg/m3) w = 11.576 N/m3

3 3
P = (20 m /s)(11.576 N/m )(110.756 m)
P = 25.642 kW

Problem 04. A fan has a total head of 190 m and a static

pressure of 200 mmwg. If the air density is 1.20 kg/m 3,
calculate the air velocity.

– static head
hs = (0.20 m)(1000 kg/m3)
1.20 kg/m3 hsa = 166.667 m
hv = h – hs = 190 – 166.667 hv = 23.333 m
hv = v2 / 2g; v2 = 2ghv
v2 = (2)(9.81 m/s2)(23.333 m) v = 21.396 m/s
Pressure Units to Pascals
atmosphere (atm) – 101325 Pa
Problem 05. Find the motor size needed to provide the
760 mmHg
forced draft service to a boiler that burns coal at the rate of
29.921 inHg
10 MT/h. The air requirement is 100,000 m 3/h with air being
14.696 psi
provided under 150 mmwg by a fan which has a mechanical
10.332 56 mWg
efficiency of 60%.
lb/in2 (psi) – 6894.757 Pa
inches of mercury (inHg) – 3386.388 158 Pa
– in terms of water
ft of water – 2989.06692 Pa
P = Qwh
mm of mercury (mmHg) – 133.321 8421 Pa
P = (100,000 m3/h)(9.81 kN/m3)(0.15 m)
millibar (mb) – 100 Pa
(3600 s/h)(0.60)
cm of water (cmwg) – 98.0665 Pa
P = 68.125 kW
torr – 1 mmHg
– in terms of air
ha = (0.15 m)(9.81 kN/m3)
Density of water 11.772 N/m3 ha = 125 m
P = (100,000 m3/h)(11.772 N/m3)(125 m)
1000 kg/m3 (3600 s/h)(0.60)
62.427 96 lb/ft3 P = 68.125 kW
8.3454 lb/gal

Discharge Units Problem 06. Air is flowing in a duct with velocity of 7.60
m/s and a static pressure of 22.5 mmwg. The duct diameter
m3/min (cmm) – 264.172 gpm is 1.2 m. Barometric pressure and temperature is at 99.4
m3/h (cmh) – 4.4029 gpm kPa, 30°C. What is the total pressure of air against which
ft3/s (cfs) – 448.831 17 gpm the fan will generate in mmwg? What is the fan’s air power?
ft3/min (cfm) – 7.480 52 gpm Use ρ = 995.718 kg/m3 for water at 30°C.

h = hs + hv hs = 22.5 mmwg
Problem 01. What power is required to keep air moving at – density of air
0.1 m/s through a 1 m by 0.6 m duct under a pressure of ρ = m/v = 99.4 kPa
750 Pa? (287.08 J/kg-K)(30 + 273 K)
ρa = 1.143 kg/m3
– head and discharge, P = ρgh; ρg = w – converting hw to ha
h= P h = 750 N/m2 hsa = (0.0225 m)(995.718 kg/m3)
w 11.772 N/m3 ha = 63.71 mw 1.143 kg/m3 hsa = 19.601 m
Q = (1 m)(0.6 m)(0.1 m/s) Q = 60 L/s hva = v2/2g = (7.60 m/s)2
P = (60 L/s)(11.772 N/m3)(63.71 m) P = 45 W (2)(9.81 m/s2) hva = 2.944 m
– also, Power = Qwh, h = p / w ha = 19.601 + 2.944 ha = 22.545 m
Power = (Q)(p) – pressure
P = (0.06 m3/s)(750 N/m2) P = 45 W p = waha = (1.143 kg/m3)(9.81 m/s2)(22.545 m)
p = 252.793 Pa
– total head, water gauge
Problem 02. A 12-hp motor is used to drive a fan that has hw = 252.793 N/m2
a total head of 20 m. If the fan efficiency is 70%, what is its 9810 N/m3 h = 25.769 mmwg
maximum capacity in cms? – check:
hw = (22.545 m)(1.143 kg/m3)
P = (12 hp)(0.70)(745.7 W/hp) 995.718 kg/m3 h = 25.880 mmwg
P = 6263.880 W
Q= 6263.880 W Discrepancy due to w = 9810 N/m3 which is not
(1.2 kg/m3)(9.81 N/kg)(20 m) correct when ρ = 995.718 kg/m3, it should be 9767.994
Q = 26.605 m3/s N/m3.

– power in terms of air

Problem 03. Calculate the air power of a fan that delivers Q = (π/4)(1.2 m)2 (7.60 m/s) Q = 8.595 m3/s
1200 cmm of air through a 1 m by 1.5 m outlet. Static w = (1.143 kg/m3)(9.81 N/kg)
pressure is 120 mmwg and density of air is 1.18 kg/m3. w = 11.213 N/m3
Pa = (8.595 m3/s)(11.213 N/m3)(22.545 m)
– static head Pa = 2172.791 W
hs = (0.12 m)(1000 kg/m3) – power in terms of water
1.18 kg/m3 hsa = 101.695 m w = (995.718 kg/m3)(9.81 N/kg)
v = 1200/60 m3/s w = 9767.994 N/m3
(1 m)(1.5 m) v = 13.333 m/s Pw = (8.595 m3/s)(9767.994 N/m3)(0.02588 m)
hv = v2/2g = (13.333 m/s)2 Pw = 2172.779 W
(2)(9.81 m/s2) hva = 9.061 m
h = hs + hv = 101.695 + 9.061 h = 110.756 m

4 Patrick D. Sta. Maria / February 26, 2023

 Industrial
Fans and Blowers Plant Design

Problem 07. The mechanical efficiency and static pressure pressure of 50 mmwg when operating at a speed of 400
of a fan are 40% and 20m of air, respectively. What is the rpm. The power input required is 2.90 kW. If 7.5 cms of air
static efficiency if the total pressure created by the fan is 25 is desired in the same fan installation, find the new pressure
m of air? of the fan.

es / hs = em / h – for 7.5 m3/s of air

es = (40%)(20 m) / 25 m N2 = (N1)(Q2 / Q1)
es = 32% N2 = (400 rpm)(7.50 / 4.70 cms)
N2 = 638.3 rpm
H2 / H1 = (N2 / N1)2
Problem 08. A small blower handles 75 cmm of air at H2 = (50 mmwg)(638.3 / 400)2
15.6°C. The static and velocity heads are 163.8 and 12.2 H2 = 127.321 mmwg
mmwg, respectively. Find the input power to the air from
the blower and the velocity of the air.
Problem 13. A fan develops a brake power of 150 kW at
– at 15.6°C: ρw = 998.98 kg/m3 1.2 kg/m3 air density. What is the new brake power of the
ρa = 1.223 kg/m3 fan if it is operated at 100 kPa, 30°C at the same speed?
ha = (163.8 + 12.2 mm)(998.98 kg/m3 )
1.223 kg/m3 ρ= 100 kPa
ha = 143.76 m (287.08 J/kg-K)(30 + 273 K)
w = (1.223 kg/m3)(9.81 N/kg) wa = 12 N/m3 ρa = 1.150 kg/m3
P = (75/60 m3/s)(12 N/m3)(143.76 m) P2 = (P1)(ρ2 / ρ1)
P = 2156.40 W P2 = (150 kW)(1.15 / 1.2) P2 = 143.75 kW
– velocity of the air, hva = 12.2 mmwg
hva = (0.0122 mwg)(998.98/1.223)
hva = 9.965 m Problem 14. A sewerage aeration blower rotating at 3500
v2 = 2gh = (2)(9.81 m/s2)(9.965 m) rpm is designed to deliver 600 cmm of air from 20°C, 1 atm
v = 13.983 m/s to 158 kPaa with an adiabatic efficiency of 65%. During
summer, the atmospheric temperature rises to 43°C but the
barometric pressure remains the same. It is desired to vary
Problem 09. A small blower handles 43.33 cmm of air the blower speed to maintain the same discharge pressure.
whose density is 1.169 kg/m3. The static and velocity heads Determine the discharge volume with the new speed.
are 163.8 and 12.2 mm, respectively. Local gravity is 9.741
m/s2. Find the power input to the air from the blower. If the h1 = Q1 2 h1 = T2
initial velocity is negligible, find the final velocity of the air. h2 Q2 h2 T1
Q2 = Q1 (T1/T2)0.5
ha = (163.8 + 12.2 mm)(1000 kg/m3 ) Q2 = (10 m3/s) 20 + 273 ^0.5
1.169 kg/m3 43 + 273 Q2 = 9.629 m3/s
ha = 150.556 m
w = (1.169 kg/m3)(9.741 m/s2)
wa = 11.387 N/m3
P = (43.33/60 m3/s)(11.387 N/m3)(150.556 m)
P = 1238.069 W
– velocity of the air, hva = 12.2 mmwg
hva = (0.0122 mwg)(1000/1.169)
hva = 10.436 m
v2 = 2gh = (2)(9.741 m/s2)(10.436 m)
v = 14.259 m/s

Problem 10. The volume flow rate delivered by a fan is 20

m3/s at 180 mmwg pressure. Air density is 1.185 kg/m3 and
the fan draws in 44 kW of power. What is the fan’s
efficiency?

ha = (180 mm)(1000 kg/m3 )

1.185 kg/m3 hS = 151.90 m
wa = (1.185 kg/m3)(9.81 m/s2)
wa = 11.625 N/m3
3 3
P = (20 m /s)(11.625 N/m )(151.90 m)
P = 35,316.75 W
eF = 35.317 / 44 eF = 80.265 %

Problem 11. Air leaves a fan through a duct at a velocity of

11.25 m/s and a discharge static pressure of 76.2 mmwg.
The fan delivers 9.45 cms of air at a density of 1.2 kg/m 3.
What is the fan efficiency if it draws 13.75 kW at the motor
coupling?

h = V2 hV = (11.25 m/s)2
2g (2)(9.81 m/s2) hV = 6.451 m
ha = (76.2 mm)(1000 kg/m3)
1.2 kg/m3 hS = 63.50 m
h = 6.451 + 63.50 h = 69.951 m
wa = (1.2 kg/m3)(9.81 m/s2) wa = 11.772 N/m3
P = (9.45 m3/s)(11.772 N/m3)(69.951 m)
P = 7781.727 W
eF = 7.78 / 13.75 eF = 56.58 %

Problem 12. A fan delivers 4.7 cms of air at a static

5 Patrick D. Sta. Maria / February 26, 2023