TEXTBOOK NOTES – OPTIMIZATION APPLICATIONS

OPTIMIZATION

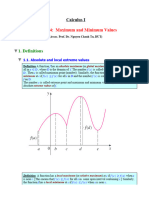
• Define the Terms: Let 𝑓𝑓 be a function that is defined for all 𝑥𝑥 in the closed interval [𝑎𝑎, 𝑏𝑏]. Let 𝑐𝑐 be a
number in the interval.

• We say that 𝑓𝑓has an absolute maximum on the interval at 𝑐𝑐 if…

• We say that 𝑓𝑓 has an absolute minimum on the interval at 𝑐𝑐 if…

• Extreme-Value Theorem: Copy the statement of the Extreme-Value Theorem in the space below.

If a function f is continuous on a closed interval [a, b], then f has both an absolute
maximum and an absolute minimum on the interval. Each of these values occurs
either at an endpoint of the interval or at a critical number of f.

APPLICATIONS

• Solving Applied Problems: Write out the steps listed in the text for solving applied optimization
problems.

Step 1 Read the problem carefully. Make sure you understand what is given and
what is asked for.

Step 2 If possible, sketch a diagram and label the various parts.

Step 3 Decide which variable is to be maximized or minimized. Express that variable as a function of
one other variable. Be sure to determine the domain
of this function.

Step 4 Find the critical numbers for the function in Step 3.

Step 5 If the domain is a closed interval, apply the extreme-value theorem: evaluate the function at
the endpoints and at each critical number to see which
yields the absolute maximum or minimum. If the domain is a (not neces-sarily closed) interval
in which there is exactly one critical number, x=c,
apply the critical-point theorem: if f has a local extremum at x=c, then
this local extremum is the absolute extremum.