Unit 2: Limit Laws

Lesson 2.2
Limits of Algebraic Functions
Contents
Introduction 1

Learning Objectives 2

Warm Up 3

Learn about It! 4

Limit of a Polynomial Function 4
Limit of a Rational Function 6
0
Evaluating Limits of Indeterminate form of Type 0 by Factoring Technique 12

Limit of a Radical Function 18

0
Evaluating Limits of Indeterminate form of Type 0 by Rationalizing Technique 20

Key Points 27

Key Formulas 28

Check Your Understanding 29

Challenge Yourself 30

Bibliography 31

Key to Try It! 32

Unit 2: Limit Laws

Lesson 2.2

Limits of Algebraic Functions

Introduction
Whenever you throw a ball upward, what do you notice? Due to gravity, any object thrown
vertically upward, after reaching maximum height, will go back down. The height ℎ reached
by any object thrown vertically upward after some time 𝑡 is given by the general formula
1
ℎ(𝑡) = 𝑣0 𝑡 − 2 𝑔𝑡 2 , where 𝑣𝑜 is the initial velocity of the object and 𝑔 is the acceleration due to

gravity, which is constant at 𝑔 = 32 ft⁄s2 . Note that this function is algebraic, particularly a
polynomial function. There are other real-life quantities that could be expressed as algebraic
functions such as speed and time, the volume of space figures and their dimensions, and
many others.

2.2. Limits of Algebraic Functions 1

Unit 2: Limit Laws

In the previous lesson, you were able to apply the limit laws in evaluating the limit of a
function. Intuitively, you already have the notion that the limit of some functions could be
solved by direct substitution.

In this lesson, we will verify if the limit of an algebraic function 𝑓(𝑥) as 𝑥 approaches 𝑐 is equal
to the value of 𝑓(𝑐).

Learning Objectives DepEd Competency

In this lesson, you should be able to do the

Apply the limit laws in evaluating
following: the limit of algebraic functions
• Prove theorems on limits of (STEM_BC11LC-IIIa-4).

algebraic functions.
• Evaluate the limits of algebraic
functions.

2.2. Limits of Algebraic Functions 2

Unit 2: Limit Laws

Warm Up

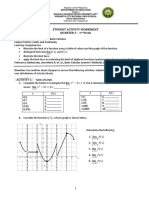
Limit in Different Ways 10 minutes

This activity will verify the limit of algebraic functions using three methods.

Materials
● calculator
● paper
● pen

Procedure
1. This activity should be done in groups of three students.
a. The first student will evaluate the limit of the given function using tables of
values.
b. The second student will evaluate the limit of the function using appropriate
limit laws.
c. The third student will evaluate the function at 𝑥 = 3.
2. Do the assigned task using the given below. Name the function as 𝑓(𝑥).
a. lim (2𝑥 2 − 5𝑥 + 1)
𝑥→3
4𝑥+2
b. lim
𝑥→3 𝑥+4

c. lim √5𝑥 + 1
𝑥→3

3. For the first student, use the table below to compute the limits of the given functions.
Left side of 3 Right side of 3
𝒙 𝒇(𝒙) 𝒙 𝒇(𝒙)
2.5 3.5
2.9 3.1
2.98 3.002
2.999 3.001

2.2. Limits of Algebraic Functions 3

Unit 2: Limit Laws

2.9999 3.0001

Guide Questions
1. What types of functions are given?
2. Compare the limits you obtained using the tables of values and limit laws. What have
you observed?
3. What function values did you get at 𝑥 = 3? Are these values equal to the limits of
these functions?

Learn about It!

Algebraic functions are functions that can be expressed using the operations addition,
subtraction, multiplication, division, and raising to a fractional power. In this lesson, limits of
three kinds of algebraic functions will be discussed. These are polynomial, rational, and
radical functions.

Is direct substitution always applicable in finding

the limit of polynomial functions? Why or why not?

Limit of a Polynomial Function

A polynomial function is a function that can be written in the form 𝑓(𝑥) = 𝑎𝑛 𝑥 𝑛 + 𝑎𝑛−1 𝑥 𝑛−1 +
𝑎𝑛−2 𝑥 𝑛−2 + ⋯ + 𝑎1 𝑥 + 𝑎𝑜 , where 𝑛 (the highest exponent of the variable) is a nonnegative
integer known as the degree and 𝑎𝑛 , 𝑎𝑛−1 , …, 𝑎0 (the coefficients of the variable) are real
numbers. Some examples of polynomial functions are 𝑦 = 2𝑥 + 1, 𝑓(𝑥) = 1 − 𝑥 2 , and
ℎ(𝑥) = 𝑥 3 + 4𝑥 + 5.

Let us use the limit laws to evaluate the limit of a polynomial function. Consider
lim (𝑥 2 + 𝑥 − 5).
𝑥→1

2.2. Limits of Algebraic Functions 4

Unit 2: Limit Laws

lim (𝑥 2 + 𝑥 − 5) = lim 𝑥 2 + lim 𝑥 + lim (−5) Sum Law

𝑥→1 𝑥→1 𝑥→1 𝑥→1
2
= (lim 𝑥) + lim 𝑥 + lim (−5)
𝑥→1 𝑥→1 𝑥→1
Power Law (lim 𝑥 2 = (lim 𝑥)2 )
𝑥→1 𝑥→1
= 12 + 1−5 Substitution (lim 𝑥 = 1)
𝑥→1
= −3

Another way of solving the limit of a polynomial function is by using the following theorem.

Theorem 2.2.1.
The limit of a polynomial function 𝑓(𝑥) as 𝑥 approaches 𝑐 is equal to 𝑓(𝑐). In symbols,

𝐥𝐢𝐦 𝒇(𝒙) = 𝒇(𝒄).

𝒙→𝒄

Proof:
Let 𝑓(𝑥) = 𝑎𝑛 𝑥 𝑛 + 𝑎𝑛−1 𝑥 𝑛−1 + 𝑎𝑛−2 𝑥 𝑛−2 + ⋯ + 𝑎1 𝑥 + 𝑎𝑜 be a polynomial function and 𝑐 be a
real number. Remember that a polynomial function is defined at any real number. Thus, if
𝑥 = 𝑐, then

𝑓(𝑐) = 𝑎𝑛 𝑐 𝑛 + 𝑎𝑛−1 𝑐 𝑛−1 + 𝑎𝑛−2 𝑐 𝑛−2 + ⋯ + 𝑎1 𝑐 + 𝑎𝑜 .

Now, let us apply the limit laws to evaluate lim 𝑓(𝑥).

𝑥→𝑐

lim 𝑓(𝑥) = lim ( 𝑎𝑛 𝑥 𝑛 + 𝑎𝑛−1 𝑥 𝑛−1 + 𝑎𝑛−2 𝑥 𝑛−2 + ⋯ + 𝑎1 𝑥 + 𝑎𝑜 )

𝑥→𝑐 𝑥→𝑐

= lim 𝑎𝑛 𝑥 𝑛 + lim 𝑎𝑛−1 𝑥 𝑛−1 + lim 𝑎𝑛−2 𝑥 𝑛−2 + lim 𝑎1 𝑥 + lim 𝑎𝑜

𝑥→𝑐 𝑥→𝑐 𝑥→𝑐 𝑥→𝑐 𝑥→𝑐
𝑛 𝑛−1 𝑛−2
= 𝑎𝑛 (lim 𝑥) + 𝑎𝑛−1 (lim 𝑥) + 𝑎𝑛−2 (lim 𝑥) + ⋯ + 𝑎1 lim 𝑥 + lim 𝑎𝑜
𝑥→𝑐 𝑥→𝑐 𝑥→𝑐 𝑥→𝑐 𝑥→𝑐
𝑛 𝑛−1 𝑛−2
= 𝑎𝑛 𝑐 + 𝑎𝑛−1 𝑐 + 𝑎𝑛−2 𝑐 + ⋯ + 𝑎1 𝑐 + 𝑎𝑜
= 𝑓(𝑐)

2.2. Limits of Algebraic Functions 5

Unit 2: Limit Laws

Therefore, 𝐥𝐢𝐦 𝒇(𝒙) = 𝒇(𝒄). The proof is done.

𝒙→𝒄

Let us use Theorem 2.2.1 to evaluate lim (𝑥 2 + 𝑥 − 5). Let 𝑓(𝑥) = 𝑥 2 + 𝑥 − 5.

𝑥→1

lim (𝑥 2 + 𝑥 − 5) = 𝑓(1)
𝑥→1
= (1)2 + 1 − 5
=1−4
= −3

Limit of a Rational Function

𝑃(𝑥)
A rational function is a function that can be written in the form 𝑓(𝑥) = 𝑄(𝑥), where 𝑃(𝑥) and

𝑄(𝑥) are both polynomials, and 𝑄(𝑥) is not equal to zero. Some examples of rational functions
1 𝑥+3 𝑥 2−4
are 𝑓(𝑥) = 𝑥+2, 𝑦 = 2𝑥−9, and ℎ(𝑥) = .
𝑥+5

3𝑥+2
Let us use the limit laws to evaluate the limit of a rational function. Consider lim 5𝑥−1.
𝑥→2

lim (3𝑥 + 2)
3𝑥 + 2 𝑥→2 Quotient Law
lim =
𝑥→2 5𝑥 − 1 lim (5𝑥 − 1)
𝑥→2
lim 3𝑥 + lim 2 Sum Law
= 𝑥→2 𝑥→2
lim 5𝑥 − lim 1
𝑥→2 𝑥→2
3 lim 𝑥 + 2
= 𝑥→2 Limit of a Constant Function
5 lim 𝑥 − 1
𝑥→2
3(2) + 2
= Limit of an Identity Function
5(2) − 1
6+2
=
10 − 1
8
=
9

Another way of solving the limit of a rational function is by using the following theorem.

2.2. Limits of Algebraic Functions 6

Unit 2: Limit Laws

Theorem 2.2.2
𝑃(𝑥) 𝑃(𝑐)
The limit of a rational function as 𝑥 approaches 𝑐 is equal to 𝑄(𝑐), provided 𝑄(𝑐) ≠ 0. In
𝑄(𝑥)

symbols,

𝑷(𝒙) 𝑷(𝒄)
𝐥𝐢𝐦 = ,
𝒙→𝒄 𝑸(𝒙) 𝑸(𝒄)
provided 𝑸(𝒄) ≠ 𝟎.

Proof:
𝑃(𝑥)
Let 𝑓(𝑥) = 𝑄(𝑥) be a rational function, where 𝑃(𝑥) and 𝑄(𝑥) are both polynomials, and
𝑃(𝑐)
𝑄(𝑥) ≠ 0. If 𝑥 = 𝑐, where 𝑐 is any real number, then we have 𝑓(𝑐) = .
𝑄(𝑐)

Now, let us use the limit laws to evaluate lim 𝑓(𝑥).

𝑥→𝑐

lim 𝑃(𝑥)
𝑥→𝑐
lim 𝑓(𝑥) =
𝑥→𝑐 lim 𝑄(𝑥)
𝑥→𝑐

Applying Theorem 2.2.1, we have

lim 𝑃(𝑥) 𝑃(𝑐)

𝑥→𝑐
= .
lim 𝑄(𝑥) 𝑄(𝑐)
𝑥→𝑐

𝑃(𝑥) 𝑃(𝑐)
Therefore, lim 𝑄(𝑥) = 𝑄(𝑐). The proof is done.
𝑥→𝑐

3𝑥+2
Let us use Theorem 2.2.2 to evaluate lim 5𝑥−1. Let 𝑃(𝑥) = 3𝑥 + 2 and 𝑄(𝑥) = 5𝑥 − 1.
𝑥→2

3𝑥 + 2 𝑃(2)
lim =
𝑥→2 5𝑥 − 1 𝑄(2)

2.2. Limits of Algebraic Functions 7

Unit 2: Limit Laws

3(2) + 2
=
5(2) − 1
6+2
=
10 − 1
8
=
9

Is direct substitution always applicable in finding

the limit of rational functions? Why or why not?

While direct substitution could be used to evaluate the limit of a rational function, some limits
of rational functions may not be solved using this method because Theorem 2.2.2 assumes
2
that the denominator is not equal to zero. Consider the function 𝑓(𝑥) = (𝑥−1)2 and solve its

limit as 𝑥 approaches 1 using tables of values.

𝒙− 𝒇(𝒙) 𝒙+ 𝒇(𝒙)
0.9 200 1.1 200
0.99 20 000 1.01 20 000
0.999 2 000 000 1.001 2 000 000
0.9999 200 000 000 1.0001 200 000 000

Observe that when 𝑥 approaches 1 from the left, the value of the function increases without
bound. This means that the limit of 𝑓(𝑥) as 𝑥 approaches to the left of 1 is positive infinity. In
symbols, lim− 𝑓(𝑥) = ∞. Likewise, it can be observed that when 𝑥 approaches 1 from the right,
𝑥→1

the value of the function increases without bound. This means that the limit of 𝑓(𝑥) as 𝑥
approaches to the right of 1 is positive infinity. In symbols, lim+ 𝑓(𝑥) = ∞. Since
𝑥→1
𝟐
𝐥𝐢𝐦 𝒇(𝒙) = 𝐥𝐢𝐦+ 𝒇(𝒙) = ∞, we can say that 𝐥𝐢𝐦 (𝒙−𝟏)𝟐 = ∞.
𝒙→𝟏− 𝒙→𝟏 𝒙→𝟏

2.2. Limits of Algebraic Functions 8

Unit 2: Limit Laws
2
We can verify this by looking at the graph of 𝑦 = (𝑥−1)2 .

Notice that the graph goes upward without bound from the left and the right with the vertical
asymptote 𝑥 = 1. This means that the left- and right-hand limits are the same.

2
Let us consider another rational function 𝑓(𝑥) = 𝑥 3 and solve its limit as 𝑥 approaches 0 using

tables of values.

𝒙− 𝒇(𝒙) 𝒙+ 𝒇(𝒙)
−0.1 −2 000 0.1 2 000
−0.01 −2 000 000 0.01 2 000 000
−0.001 −2 000 000 000 0.001 2 000 000 000
−0.0001 −2 000 000 000 000 0.0001 2 000 000 000 000

It could be seen from the table that when 𝑥 approaches 0 from the left, the value of the
function decreases without bound. This means that the limit of 𝑓(𝑥) as 𝑥 approaches to the
left of 0 is negative infinity. In symbols, lim− 𝑓(𝑥) = −∞. On the other hand, when 𝑥
𝑥→0

approaches 0 from the right, the value of the function increases without bound. This means

2.2. Limits of Algebraic Functions 9

Unit 2: Limit Laws

that the limit of 𝑓(𝑥) as 𝑥 approaches to the right of 0 is positive infinity. In symbols,
lim 𝑓(𝑥) = ∞. Since
𝑥→0+
𝟐
𝐥𝐢𝐦− 𝒇(𝒙) ≠ 𝐥𝐢𝐦+ 𝒇(𝒙), we can say that 𝐥𝐢𝐦 𝒙𝟑 does not exist.
𝒙→𝟎 𝒙→𝟎 𝒙→𝟎

2
We can verify this by looking at the graph of 𝑦 = 𝑥 3 .

The graph goes upward without bound from the right, and downward without bound from
the left with the vertical asymptote 𝑥 = 0. This means that the left- and right-hand limits are
not equal.

Remember
𝑃(𝑥)
Given a rational function of the form 𝑓 (𝑥) = , where 𝑛 is a
[𝑄(𝑥)]𝑛

positive integer, and 𝑃(𝑥) and 𝑄(𝑥) are both polynomials, the
following statements are always TRUE for any real number 𝑐,
provided 𝑃(𝑐) ≠ 0 and 𝑄(𝑐) = 0.
1. If 𝑃(𝑐) > 0 and 𝑛 is even, then lim 𝑓(𝑥) = ∞.
𝑥→𝑐

2. If 𝑃(𝑐) < 0 and 𝑛 is even, then lim 𝑓(𝑥) = −∞.

𝑥→𝑐

2.2. Limits of Algebraic Functions 10

Unit 2: Limit Laws

3. If 𝑛 is odd, then lim 𝑓(𝑥) does not exist.

𝑥→𝑐

𝑃(𝑥)
Given a rational function 𝑓 (𝑥 ) = 𝑄(𝑥), can we apply
the previous method in determining lim 𝑓(𝑥) if
𝑥→𝑐
𝑃(𝑐 ) = 𝑄(𝑐 ) = 0? Why or why not?

0
There are other rational functions whose function value at 𝑥 = 𝑐 is 0. We call this function
0
indeterminate. Indeterminate form of type 0 happens when there is common factor

between the numerator and denominator whose value is zero at 𝑥 = 𝑐.

𝑥
Consider the function 𝑓(𝑥) = 𝑥 2−𝑥. The function value at 𝑥 = 0 does not exist since:

𝑥
𝑓(𝑥) =
𝑥2 − 𝑥
0
𝑓(0) = 2
0 −0
0
=
0

This happens since a factor, which is 𝑥, is common to the numerator and denominator of
the function.

𝑥
𝑓(𝑥) =
𝑥2
−𝑥
𝑥(1)
𝑓(𝑥) =
𝑥(𝑥 − 1)

The value of this factor is zero at 𝑥 = 0 making both the numerator and denominator equal
to 0. The effect of this factor could be seen below, which makes a hole in the graph.

2.2. Limits of Algebraic Functions 11

Unit 2: Limit Laws

𝟎
Evaluating Limits of Indeterminate form of Type 𝟎 by Factoring Technique
0
To evaluate limits of indeterminate form of rational functions of type 0 by factoring, we follow

these general steps:

1. Factor the numerator and denominator and simplify the expression by eliminating the
common factors.
2. Evaluate the limit of the resulting expression.

𝑥
Let us solve lim 𝑥 2−𝑥.
𝑥→0

Since, we already know that the function is indeterminate, we follow the given steps to
evaluate its limit.

𝑥 𝑥(1)
=
𝑥2 − 𝑥 𝑥(𝑥 − 1)
1
=
𝑥−1
1 1
lim =
𝑥→0 𝑥 − 1 0−1

2.2. Limits of Algebraic Functions 12

Unit 2: Limit Laws
1
=
−1
= −1

𝑥
Thus, lim 𝑥 2 −𝑥 = −1.
𝑥→0

Let’s Practice!

Example 1
Evaluate lim (−2𝑥 4 + 5𝑥 3 − 7𝑥 2 + 9𝑥 − 1).
𝑥→−2

Solution
Solve using Theorem 2.2.1.

lim (−2𝑥 4 + 5𝑥 3 − 7𝑥 2 + 9𝑥 − 1) = −2(−2)4 + 5(−2)3 − 7(−2)2 + 9(−2) − 1

𝑥→−2
= −2(16) + 5(−8) − 7(4) − 18 − 1
= −32 − 40 − 28 − 18 − 1
= −119

Thus, lim (−2𝑥 4 + 5𝑥 3 − 7𝑥 2 + 9𝑥 − 1) = −𝟏𝟏𝟗.

𝑥→−2

1 Try It!
Evaluate lim (2𝑦 5 − 12𝑦 3 + 8𝑦 2 − 13).
𝑦→3

2.2. Limits of Algebraic Functions 13

Unit 2: Limit Laws

Example 2
𝑧 2+5
Solve lim 4𝑧−7.
𝑧→9

Solution
Solve using Theorem 2.2.2.

𝑧 2 + 5 (9)2 + 5
lim =
𝑧→9 4𝑧 − 7 4(9) − 7
81 + 5
=
36 − 7
86
=
29

𝑧 2+5 𝟖𝟔
Thus, lim 4𝑧−7 = 𝟐𝟗.
𝑧→9

2 Try It!
11−5𝑎−2𝑎 2
Solve lim .
𝑎→−4 𝑎+5

Example 3
𝑓(𝑥)
If 𝑓(𝑥) = 2𝑥 + 5 and 𝑔(𝑥) = (𝑥 2 − 2𝑥 + 1)3 , find lim 𝑔(𝑥).
𝑥→1

Solution
𝑓(𝑥)
Step 1: Substitute the values of 𝑓(𝑥) and 𝑔(𝑥) into lim 𝑔(𝑥).
𝑥→1

𝑓(𝑥) 2𝑥 + 5
lim = lim 2
𝑥→1 𝑔(𝑥) 𝑥→1 (𝑥 − 2𝑥 + 1)3

𝑃(𝑥)
The resulting function is a rational function of the form ℎ(𝑥) = [𝑄(𝑥)]𝑛 , where

𝑃(1) = 2(1) + 5 = 7 > 0 and 𝑛 is an odd number. However, we can rewrite the

2.2. Limits of Algebraic Functions 14

Unit 2: Limit Laws

denominator as [(𝑥 − 1)2 ]3 , making it (𝑥 − 1)6 .

Step 2: Determine whether the denominator is zero if 𝑥 = 1.

𝑔(𝑥) = 𝑥 − 1
𝑔(1) = 1 − 1
=0

Since the denominator is zero if 𝑥 = 1, we cannot use Theorem 2.2.2. Instead,

we use the property of the limit of rational functions that can be written in the
𝑃(𝑥)
form 𝑓(𝑥) = [𝑄(𝑥)]𝑛 .

Step 3: Solve the limit of the function.

𝑃(𝑥)
The limit of a rational function 𝑓(𝑥) = [𝑄(𝑥)]𝑛 , where 𝑃(𝑐) > 0 and 𝑛 is even, as 𝑥
2𝑥+5
approaches is positive infinity. Thus, lim (𝑥 2 −2𝑥+1)3 = ∞.
𝑥→1

3 Try It!
1 𝑓(𝑥)
If 𝑓 (− 2) = 25 and 𝑔(𝑥) = (4𝑥 2 + 4𝑥 + 1)5 , find lim1 𝑔(𝑥).
𝑥→−2

2.2. Limits of Algebraic Functions 15

Unit 2: Limit Laws

Example 4
2𝑥 3+3𝑥 2−2𝑥−3
Evaluate lim3 2 .
𝑥→−2 6𝑥 +11𝑥+3

Solution
3
Step 1: Verify if the function is indeterminate at 𝑥 = − 2.

2𝑥 3 + 3𝑥 2 − 2𝑥 − 3
𝑓 (𝑥) =
6𝑥 2 + 11𝑥 + 3
3 3 3 2 3
3 2 (− 2) + 3 (− 2) − 2 (− 2) − 3
𝑓 (− ) =
2 3 2 3
6 (− 2) + 11 (− 2) + 3
27 9
2 (− 8 ) + 3 (4) + 3 − 3
=
9 33
6 (4) − 2 + 3
27 27
− 4 + 4
=
54 33
− +3
4 2
0
=
54 − 66 + 12
4
0
=
0
4
0
=
0

Thus, the function is indeterminate.

Step 2: Simplify the function by factoring and evaluate the limit of the resulting
expression.

2𝑥 3 + 3𝑥 2 − 2𝑥 − 3 (𝑥 + 1)(𝑥 − 1)(2𝑥 + 3)
=
6𝑥 2 + 11𝑥 + 3 (2𝑥 + 3)(3𝑥 + 1)

2.2. Limits of Algebraic Functions 16

Unit 2: Limit Laws

𝑥2 − 1
=
3𝑥 + 1
3 2
𝑥 2 − 1 (− 2) − 1
lim =
𝑥→−2 3𝑥 + 1
3 3
3 (− 2) + 1
9
−1
= 4
9
−2 +1
5
= 4
7
−2
5 2
= (− )
4 7
5
=−
14

𝟐𝒙𝟑 +𝟑𝒙𝟐 −𝟐𝒙−𝟑 𝟓

Thus, 𝐥𝐢𝐦𝟑 = − 𝟏𝟒.
𝟔𝒙𝟐 +𝟏𝟏𝒙+𝟑
𝒙→−𝟐

4 Try It!
𝑥 4−16
Evaluate lim .
𝑥→−2 2𝑥 2+9𝑥+10

2.2. Limits of Algebraic Functions 17

Unit 2: Limit Laws

Limit of a Radical Function

A radical function is a function having a polynomial under the radical sign. Some examples
of rational functions are 𝑓(𝑥) = √𝑥 + 2, 𝑦 = √𝑥 2 − 5, and ℎ(𝑥) = 9 √2𝑥 − 7.
3 4

Let us use the limit laws to evaluate the limit of a radical function. Consider lim √7𝑥 + 1.
𝑥→5

lim √7𝑥 + 1 = √ lim (7𝑥 + 1) Root Law

𝑥→5 𝑥→5

= √ lim 7𝑥 + lim 1 Sum Law

𝑥→5 𝑥→5

= √7 lim 𝑥 + 1 Constant Multiple Law, Limit of a Constant Function

𝑥→5

= √7(5) + 1 Limit of an Identity Function

= √35 + 1
= √36
=6

Another way of solving the limit of a radical function is by using the following theorem.

Theorem 2.2.3
If 𝑓(𝑥) = 𝑛√𝑃(𝑥), where 𝑃(𝑥) is a polynomial in 𝑥, then lim 𝑛√𝑃(𝑥) = 𝑛√𝑃(𝑐) for any real
𝑥→𝑐

number 𝑐.

𝐥𝐢𝐦 𝑛√𝑃(𝑥) = 𝑛√𝑃(𝑐)

𝒙→𝒄

Proof:
Let 𝑓(𝑥) = 𝑛√𝑃(𝑥) be a radical function, where 𝑃(𝑥) is a polynomial in 𝑥. If 𝑥 = 𝑐, where 𝑐 is

any real number, then 𝑓(𝑐) = 𝑛√𝑃(𝑐).

2.2. Limits of Algebraic Functions 18

Unit 2: Limit Laws

Now, let us use the limit laws to evaluate lim 𝑓(𝑥).

𝑥→𝑐

𝑛
lim 𝑓(𝑥) = lim √𝑃(𝑥)
𝑥→𝑐 𝑥→𝑐

= 𝑛√ lim 𝑃(𝑥)
𝑥→𝑐

Applying Theorem 2.2.1,

𝑛
lim √𝑃(𝑥) = 𝑛√𝑃(𝑐).
𝑥→𝑐

Therefore, lim √𝑃(𝑥) = 𝑛√𝑃(𝑐). The proof is done.

𝑛
𝑥→𝑐

Let us use Theorem 2.2.3 to evaluate lim √7𝑥 + 1.

𝑥→5

lim √7𝑥 + 1 = √7(5) + 1

𝑥→5

= √35 + 1
= √36
=6

There are also times when a radical function could be indeterminate. Consider the function
𝑥−1
𝑓(𝑥) = and evaluate it at 𝑥 = 1.
√𝑥−1

𝑥−1
𝑓(𝑥) =
√𝑥 − 1
1−1
𝑓(1) =
√1 − 1
0
=
0

2.2. Limits of Algebraic Functions 19

Unit 2: Limit Laws

What is the conjugate of √𝑥 + 1 + √𝑥 − 1?

𝟎
Evaluating Limits of Indeterminate form of Type 𝟎 by Rationalizing Technique
0
To evaluate limits of indeterminate form of radical functions of type by rationalizing, we
0

follow these three cases, and evaluate the simplified expression.

1. Rationalize the denominator if only the denominator has a radical expression.

2. Rationalize the numerator if only the numerator has a radical expression.
3. Rationalize both numerator and denominator if the two have radical expressions.

𝑥−1
Let us solve lim .
𝑥→0 √𝑥−1

We already know that the function is indeterminate. Since only the denominator has a
radical expression, then we simplify this by rationalizing the denominator and evaluate the
simplified expression.

𝑥−1 √𝑥 + 1 (𝑥 − 1)(√𝑥 + 1)
∙ =
√𝑥 − 1 √𝑥 + 1 (√𝑥 − 1)(√𝑥 + 1)
(𝑥 − 1)(√𝑥 + 1)
=
(𝑥 − 1)
= √𝑥 + 1

lim (√𝑥 + 1) = √0 + 1
𝑥→0
=0+1
=1

𝑥−1
Thus, lim = 1.
𝑥→0 √𝑥−1

2.2. Limits of Algebraic Functions 20

Unit 2: Limit Laws

Example 5
Evaluate lim √5𝑥 3 − 7𝑥 2 + 2.
𝑥→4

Solution
Solve using Theorem 2.2.3.

lim √5𝑥 3 − 7𝑥 2 + 2 = √5(4)3 − 7(4)2 + 2

𝑥→4

= √5(64) − 7(16) + 2
= √320 − 112 + 2
= √210

Thus, lim √5𝑥 3 − 7𝑥 2 + 2 = √𝟐𝟏𝟎.

𝑥→4

5 Try It!
Evaluate lim3 √4𝑦 2 + 24𝑦 + 27.
3

𝑦→−2

Example 6
3𝑥+5 𝑓(𝑥)𝑔(𝑥)
If 𝑓(𝑥) = 𝑥 2 + 1, 𝑔(𝑥) = √9𝑥 + 2, and ℎ(𝑥) = , evaluate lim .
𝑥−1 𝑥→8 ℎ(𝑥)

Solution
𝑓(𝑥)𝑔(𝑥)
Step 1: Simplify .
ℎ(𝑥)

𝑓(𝑥)𝑔(𝑥) (𝑥 2 + 1)√9𝑥 + 2
=
ℎ(𝑥) 3𝑥 + 5
𝑥−1
2
(𝑥 + 1)(𝑥 − 1)√9𝑥 + 2
=
3𝑥 + 5

2.2. Limits of Algebraic Functions 21

Unit 2: Limit Laws

Step 2: Evaluate the limit of the resulting function.

(𝑥 2 + 1)(𝑥 − 1)√9𝑥 + 2 (82 + 1)(8 − 1)√9(8) + 2

lim =
𝑥→8 3𝑥 + 5 3(8) + 5
(64 + 1)(7)√72 + 2
=
24 + 5
65(7)√74
=
29
455√74
=
29

(𝑥 2+1)(𝑥−1)√9𝑥+2 𝟒𝟓𝟓√𝟕𝟒
Thus, lim = .
𝑥→8 3𝑥+5 𝟐𝟗

6 Try It!
ℎ(𝑥)𝑔(𝑥)
Using the same functions in Example 7, evaluate lim .
𝑥→2 𝑓(𝑥)

Example 7
√𝑥+2−3
Evaluate lim .
𝑥→7 𝑥−7

Solution
Step 1: Verify if the function is indeterminate at 𝑥 = 7.

√𝑥 + 2 − 3
𝑓(𝑥) =
𝑥 −7
√7 + 2 − 3
𝑓(7) =
7−7
√9 − 3
=
0
3−3
=
0
0
=
0

2.2. Limits of Algebraic Functions 22

Unit 2: Limit Laws

Step 2: Evaluate the limit by rationalizing technique.

Since only the numerator has a radical expression, then we simplify this by
rationalizing the numerator, and evaluate the simplified expression.

√𝑥 + 2 − 3 √𝑥 + 2 + 3 (√𝑥 + 2 − 3)(√𝑥 + 2 + 3)
∙ =
𝑥 −7 √𝑥 + 2 + 3 (𝑥 − 7)(√𝑥 + 2 + 3)
𝑥+2−9
=
(𝑥 − 7)(√𝑥 + 2 + 3)
(𝑥 − 7)
=
(𝑥 − 7)(√𝑥 + 2 + 3)
1
=
√𝑥 + 2 + 3
1 1
lim =
𝑥→7 √𝑥 +2+3 √7 + 2 + 3
1
=
√9 + 3
1
=
3+3
1
=
6

√𝒙+𝟐−𝟑 𝟏
Thus, 𝐥𝐢𝐦 = 𝟔.
𝒙→𝟕 𝒙−𝟕

7 Try It!
4−√2𝑥+6
Evaluate lim .
𝑥→5 𝑥−5

2.2. Limits of Algebraic Functions 23

Unit 2: Limit Laws

Example 8
√𝑥−1
What is the value of lim ?
𝑥→1 √𝑥+3−2

Solution
Step 1: Verify if the function is indeterminate at 𝑥 = 1.

√𝑥 − 1
𝑓(𝑥) =
√𝑥 + 3 − 2
√1 − 1
𝑓(1) =
√1 + 3 − 2
1−1
=
√4 − 2
0
=
2−2
0
=
0

Step 2: Evaluate the limit by rationalizing technique.

Since both the numerator have radical expressions, we simplify this by

rationalizing the two, and evaluate the simplified expression.

√𝑥 − 1 √𝑥 + 1 √𝑥 + 3 + 2 (√𝑥 − 1)(√𝑥 + 1)(√𝑥 + 3 + 2)

∙ ∙ =
√𝑥 + 3 − 2 √𝑥 + 1 √𝑥 + 3 + 2 (√𝑥 + 3 − 2)(√𝑥 + 3 + 2)(√𝑥 + 1)
(𝑥 − 1)(√𝑥 + 3 + 2)
=
(𝑥 + 3 − 4)(√𝑥 + 1)
(𝑥 − 1)(√𝑥 + 3 + 2)
=
(𝑥 − 1)(√𝑥 + 1)
√𝑥 + 3 + 2
=
√𝑥 + 1

2.2. Limits of Algebraic Functions 24

Unit 2: Limit Laws

√𝑥 + 3 + 2 √1 + 3 + 2
lim =
𝑥→1 √𝑥 + 1 √1 + 1
√4 + 2
=
1+1
2+2
=
2
4
=
2
=2

√𝒙−𝟏
Thus, 𝐥𝐢𝐦 = 𝟐.
𝒙→𝟏 √𝒙+𝟑−𝟐

8 Try It!
√3𝑥−5−5
What is the value of lim ?
𝑥→10 3−√𝑥−1

Example 9
An object was thrown vertically upward at a speed of 80 ft/s. Determine the limit of the
function ℎ(𝑡) that represents the height of the object after 𝑡 seconds as time approaches three
seconds.

Solution
Step 1: Analyze the problem.

Recall from the introduction that the height ℎ of any object thrown vertically
1
upward is given by the function ℎ(𝑡) = 𝑣0 𝑡 − 2 𝑔𝑡 2 , where 𝑣𝑜 is the initial velocity

of the object and 𝑔 is the acceleration due to gravity, which is constant at

𝑔 = 32 ft⁄s2 .

2.2. Limits of Algebraic Functions 25

Unit 2: Limit Laws

Step 2: Identify the given information.

Based on the problem, we have the following given:

Initial velocity of the object: 𝑣0 = 80 ft/s

Acceleration due to gravity: 𝑔 = 32 ft⁄s2
1
Function that represents the height of the object: ℎ(𝑡) = 80𝑡 − 2 (32)𝑡 2 or

ℎ(𝑡) = 80𝑡 − 16𝑡 2 .

Step 3: Evaluate lim ℎ(𝑡), where ℎ(𝑡) = 80𝑡 − 16𝑡 2 .

𝑡→3

Since ℎ is a polynomial function, we can use Theorem 2.2.1.

lim ℎ(𝑡) = lim(80𝑡 − 16𝑡 2 )

𝑡→3 𝑡→3
= 80(3) − 16(3)2
= 240 − 16(9)
= 240 − 144
= 96

Thus, the limit of the function ℎ(𝑡) as 𝑡 approaches three seconds is 96 𝐟𝐭.

9 Try It!
A cylindrical water tank is to be made such that the radius is three meters longer
than the height. Determine the limit of its volume as its height approaches eight
meters.

2.2. Limits of Algebraic Functions 26

Unit 2: Limit Laws

Key Points
_____________________________________________________________________________________________

● The limit of a polynomial function 𝒇(𝒙) as 𝑥 approaches 𝑐 is equal to 𝒇(𝒄).

𝑷(𝒙) 𝑷(𝒄)
● The limit of a rational function as 𝑥 approaches 𝑐 is equal to 𝑸(𝒄), provided that
𝑸(𝒙)

𝑄(𝑐) ≠ 0.
● The limit of a radical function 𝑓(𝑥) = 𝑛√𝑃(𝑥), where 𝑃(𝑥) is a polynomial in 𝑥, as 𝑥
approaches 𝑐 is 𝑛√𝑃(𝑐) for any real number 𝑐. If 𝑛 is even, then 𝑃(𝑐) ≥ 0.
● We can use factoring and rationalizing technique to evaluate indeterminate
𝟎
forms of functions of type 𝟎. To verify if the function is indeterminate, evaluate it

at 𝑥 = 𝑐.
_____________________________________________________________________________________________

2.2. Limits of Algebraic Functions 27

Unit 2: Limit Laws

Key Formulas
_____________________________________________________________________________________________

Concept Formula Description

Limit of a Use this formula to find the

Polynomial lim 𝑓(𝑥) = 𝑓(𝑐)
𝑥→𝑐
limit of polynomial
Function functions.

Use this formula to find the

limit of rational functions
Limit of a Rational 𝑃(𝑥) 𝑃(𝑐)
lim = where 𝑃(𝑥) and 𝑄(𝑥) are
Function 𝑥→𝑐 𝑄(𝑥) 𝑄(𝑐)
both polynomials and
𝑄(𝑐) ≠ 0.

Use this formula to find the

limit of radical functions
Limit of a Radical
where 𝑃(𝑥) is a polynomial
𝑛 𝑛
lim √𝑃(𝑥) = √𝑃(𝑐)
Function 𝑥→𝑐
in 𝑥, and 𝑃(𝑐) ≥ 0 when 𝑛 is
even.

_____________________________________________________________________________________________

2.2. Limits of Algebraic Functions 28

Unit 2: Limit Laws

Check Your Understanding

A. Evaluate the following limits.

1. lim (2𝑦 2 − 5𝑦 + 1)
𝑦→2
𝑡 3 −1
2. lim
𝑡→1 𝑡−1

3. lim (7𝑥 2 − 12𝑥)

𝑥→3
2𝑥−1
4. lim
𝑥→−2 𝑥+3
3−2𝑠
5. lim 𝑠2 +5
𝑠→4
𝑥 2+6𝑥
6. lim
𝑥→−1 2−𝑥+3𝑥 2
𝑥 2−𝑥−6
7. lim 𝑥 2+𝑥−12
𝑥→3

8. lim √6𝑥 2 − 6
𝑥→−5

9. lim √2𝑥 3 + 7𝑥
3

𝑥→4
2𝑥+16
10. lim
𝑥→−8 √9−2𝑥−5

11. lim1(𝑦 5 − 8𝑦 3 + 7)
𝑦→2

10+3𝑦4
12. lim 3 −7𝑦2 +2𝑦
𝑦→−3 𝑦

𝑥 5−𝑥 4 +3𝑥
13. lim
𝑥→−2 10𝑥+5

14. lim(√3𝑡 + √5𝑡 + 1)

𝑡→3
√9−𝑠−4
15. lim
𝑠→−7 2𝑠+14

16. lim √𝑥 2 + 3𝑥 + 9
𝑥→2
𝑥+3
17. lim − (𝑥−5)3
𝑥→5
√𝑥−3
18. lim −√2𝑥+7+5
𝑥→9
12−7𝑥 4+𝑥 3
19. lim
𝑥→4 6𝑥−7
2𝑦3 −3𝑦2 +4𝑦+1
20. lim 𝑦2 +5𝑦+6
𝑦→5

2.2. Limits of Algebraic Functions 29

Unit 2: Limit Laws

B. Analyze and solve the following problems.

1. A box has a length three inches longer than twice the width and has a height five
inches longer than the width. Determine the limit of the volume of the box as the
width approaches 10 inches.
2. A soccer ball was thrown vertically upward at a velocity of 56 ft/s. Determine the limit
of the height of the ball as time approaches 2.5 seconds.

Challenge Yourself
5 8 8
A. Given 𝑓(𝑥) = 𝑥 2, 𝑔(𝑥) = (𝑥+1)3, and ℎ(𝑥) = − (𝑥 2+2𝑥+1)3 , verify if the

following limits exist.

1. lim 𝑓(𝑥)𝑔(𝑥)
𝑥→0

2. lim 𝑓(𝑥)𝑔(𝑥)
𝑥→−1

3. lim 𝑔(𝑥)ℎ(𝑥)
𝑥→−1

B. Suppose 𝑓(𝑥) is a function formed by performing exactly one of the four

3
fundamental operations using the functions 𝑔(𝑥) = (𝑥+3)3 and
(𝑥 2+6𝑥+9)2
ℎ(𝑥) = . Determine 𝑓(𝑥) if:
10

4. lim 𝑓(𝑥) = 0.
𝑥→−3

5. lim 𝑓(𝑥) does not exist.

𝑥→−3

2.2. Limits of Algebraic Functions 30

Unit 2: Limit Laws

Bibliography
Balmaceda, Jose Maria P. Basic Calculus. Quezon City: Commission on Higher Education, 2016.

Edwards, C.H., and David E. Penney. Calculus: Early Transcendentals. 7th ed. Upper Saddle
River, New Jersey: Pearson/Prentice Hall, 2008.

Larson, Ron H., and Bruce H. Edwards. Essential Calculus: Early Transcendental Functions.
Boston: Houghton Mifflin, 2008.

Leithold, Louis. The Calculus 7. New York: HarperCollins College Publ., 1997.

“Limits of Polynomial and Rational Functions.” CK-12 Foundation. Retrieved 14 January 2020
from https://www.ck12.org/book/ck-12-calculus-concepts/section/2.5/.

Smith, Robert T., and Roland B. Milton. Calculus. New York: McGraw Hill, 2012.

Tan, Soo T. Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach.
Australia: Brooks/Cole Cengage Learning, 2012.

2.2. Limits of Algebraic Functions 31

Unit 2: Limit Laws

Key to Try It!

1. 221
2. −1
3. ∞
4. −32
5. 1
22√5
6.
5
1
7. −4
9
8. −5

9. 968𝜋 cubic meters

2.2. Limits of Algebraic Functions 32