Differentiability

Example: Let and be any complex number. Calculate the value of

.
Solution: Here we have

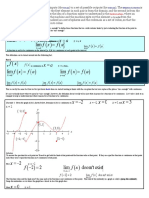
Note: We know that is continuous at some point if and

only if and both are continuous at . But this fact is not true in case of
differentiability.

Exercise: Is , differentiable anywhere?

Claim ‘Continuity does not imply differentiability’ .
Theorem: Differentiability of at any point implies the continuity of the function at
the same point.
 ANALYTICITY
• Definition: Let be a function, where is a region in , and
Then the function is said to be analytic at if is differentiable
in some (atleast one) neighborhood of .
• The function is said to be analytic on if is analytic at every point of
.
• An entire is a function which is analytic on the whole complex plane .
• Example:
Cauchy Riemann (CR) equations:
Suppose that , then the CR equations
are given by
Theorem

(Necessary Condition)

(Sufficient Condition)

Example (Necessary Condition): The polynomial function is

analytic for all and can be written as .
Thus, and
Check CR equation for any point .
Ex: Show that

is not differentiable at , though Cauchy-Riemann equations hold good at the

origin.
 Contrapositive of the 1st statement of previous theorem: If the CR equations are not
satisfied at any point , then the function is not
differentiable at that point.
Check with .

Example (Sufficient Condition): Show that The function

is differentiable for all
To show this, we first write and and
compute the partial derivatives: and
.
We see that and are all continuous functions and that the Cauchy
Riemann equations hold for all values of . Hence

Note: If exists, then it can be written as any of the following forms:

Note: Let is analytic in a domain . If the real part or imaginary part or
argument (arg ) or modulus ( ) of is constant then is constant in
.

These functions are Popularly known as Potential Functions in engineering

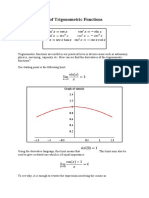
Example: The function is analytic.
The functions and are harmonic in any
domain of the complex plane.