Pumps (Part 2)

Dexter Lyndon Sabusap

Instructor

ME531B Fluid Machinery

 REMINDER

This material is ONLY for educational use of students of

the Mechanical Engineering Department of Adamson
University, Manila, Philippines.

This material is NOT for distribution or sale.

This material cannot be shared, either in print or

electronically, to people not associated with the
University.
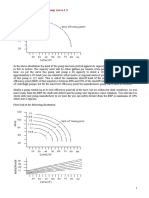
Pump Performance Curves
• The only solid indicator of a pump’s performance lies in
extensive testing.
• The device used to determine a pump’s performance is
called a pump test rig.
Pump Performance Curves
• A pump performance curve is constructed from a
number of pump testing.

• Performance charts or curves are almost always

plotted for constant shaft rotation speed 𝑁 (usually in
rev/min).

• The basic independent variable is taken to be discharge

𝑄 (in gal/min usually for liquids and ft^3/min for gases).
Pump Performance Curves
• The dependent variables, or “output,” are taken to be
total dynamic head, often simply referred to as head H
(we use pressure rise Δp for gases), brake power (BP or
bp or P) or brake horsepower (bhp), and pump
efficiency 𝜂𝑝𝑢𝑚𝑝 or η.

• The chart shown in the next slide shows a typical pump

performance curve for a centrifugal pump.
Pump Performance Curves
• The head is approximately constant at low discharge
and then drops to zero at 𝑄 = 𝑄𝑚𝑎𝑥 . At this speed and
impeller size, the pump cannot deliver any more fluid
than 𝑄𝑚𝑎𝑥 .

• The positive slope part of the head is shown dashed;

this region can be unstable and can cause hunting for
the operating point.
Pump Performance Curves
• The efficiency η is always zero at no flow and at 𝑄𝑚𝑎𝑥 .

• The efficiency η reaches a maximum at around 80 to 90

percent, at about 0.6𝑄𝑚𝑎𝑥 . This is the design flow rate
𝑄 ∗ or best efficiency point (BEP), 𝜂 = 𝜂𝑚𝑎𝑥 .

• The head and horsepower at BEP will be termed 𝐻 ∗ and

𝑃∗ (or bhp*), respectively.
Pump Performance Curves
• It is desirable that the efficiency curve be flat near
𝜂𝑚𝑎𝑥 , so that a wide range of efficient operation is
achieved. However, some designs simply do not
achieve flat efficiency curves.
Actual Pump Performance Curves
• The chart shown in the next slide shows an actual
pump performance curve for a commercial centrifugal
pump.

• The curve shown is for a basic casing size with three

different impeller diameters.

• The head curves 𝐻 𝑄 are shown in blue, but the

horsepower and efficiency curves have to be inferred
from the contour plots.
Actual Pump Performance Curves
• Everything is plotted raw [𝐻 in feet, 𝐵𝑃 in horsepower,
and 𝑄 in gallons per minute (1 U.S. gal = 231 in^3)] since
it is to be used directly by designers.

• In the next slide, a pump curve is shown for another

pump of the same design with a 20 percent larger
casing, a lower speed, and three larger impeller
diameters.
Actual Pump Performance Curves
• Comparing the two pumps may be a little confusing:
The larger pump produces exactly the same discharge
but only half the horsepower and half the head. This
will be readily understood from the scaling or similarity
laws which we will later formulate. But first, we need
to understand cavitation.
Cavitation
• Basically, pump cavitation is the boiling of the liquid at
the pump suction due to the lowering of pressure at
the eye of the impeller.

• Generally, we want to avoid cavitation in our pump.

Bubbles formed during cavitation erupts inside the high
pump and leads to pitting of the impeller blades.
Cavitation
Net Positive Suction Head
• The net positive-suction head required (NPSHR) is the
is the minimum head required at the pump inlet to
keep the liquid from cavitating at the pump inlet. This
information is obtained from the pump performance
curve and this is also experimentally determined.

• To determine whether a particular pump setup will lead

to cavitation, we calculate what we call the net
positive-suction head available (NPSHA).
Net Positive Suction Head
• As a designer, out goal is to make sure that the
𝑁𝑃𝑆𝐻𝑅 ≤ 𝑁𝑃𝑆𝐻𝐴. In words, we must make sure that
the available NPSH is greater than (or at least equal to)
the required NPSH.
Net Positive Suction Head
• For a given pump setup, the NPSHA can be calculated
as:
𝑃𝑖𝑛𝑙𝑒𝑡 𝑉𝑖𝑛𝑙𝑒𝑡 2 𝑝𝑣𝑎𝑝𝑜𝑟
𝑁𝑃𝑆𝐻𝐴 = + −
𝛾 2𝑔 𝛾

where 𝑃𝑖𝑛𝑙𝑒𝑡 and 𝑉𝑖𝑛𝑙𝑒𝑡 are the absolute pressure and

velocity at pump inlet, and 𝑃𝑣𝑎𝑝𝑜𝑟 is the absolute vapor
pressure of the liquid at the given temperature 𝑇. 𝑃𝑣𝑎𝑝𝑜𝑟
is read from the Steam Table, i.e. 𝑃𝑣𝑎𝑝𝑜𝑟 = 𝑃𝑠𝑎𝑡@𝑇 .
NOTE: Here we use the pump centerline as the datum
line which means that 𝑧𝑖𝑛𝑙𝑒𝑡 = 0.
Net Positive Suction Head
• If the pump draws water from a reservoir whose free
surface is at a height 𝑍𝑎 with respect to the pump
centerline and at absolute pressure 𝑃𝑎 , we can rewrite
NPSHA as:
𝑃𝑎 𝑝𝑣𝑎𝑝𝑜𝑟
𝑁𝑃𝑆𝐻𝐴 = ± 𝑍𝑎 − 𝐻𝑓,𝑠𝑢𝑐𝑡𝑖𝑜𝑛 −
𝛾 𝛾
where 𝐻𝑓,𝑠𝑢𝑐𝑡𝑖𝑜𝑛 is the friction head loss between the
reservoir and the pump inlet, i.e. head loss at suction
pipe. NOTE: Here we use the pump centerline as the
datum line which means that 𝑧𝑖𝑛𝑙𝑒𝑡 = 0.
Net Positive Suction Head
• Knowing 𝑃𝑎 and 𝐻𝑓,𝑠𝑢𝑐𝑡𝑖𝑜𝑛 , we can set the pump at a
height 𝑍𝑎 with respect to the reservoir free surface
that will keep 𝑁𝑃𝑆𝐻𝑅 ≤ 𝑁𝑃𝑆𝐻𝐴.

• In generally better for the pump inlet to be below the

reservoir free surface, i.e. 𝑍𝑎 > 0.

• If the pump inlet is above the reservoir free surface, i.e.

𝑍𝑎 < 0, then there is possibility that 𝑁𝑃𝑆𝐻𝑅 > 𝑁𝑃𝑆𝐻𝐴
which is NOT good because cavitation can occur in such
a case.
Net Positive Suction Head
The NPSH margin describes the safety factor by which
NPSHA must exceed NPSHR to avoid cavitation. It can be
quoted in two ways:
• As a ratio of NPSHA to NPSHR. For example, an NPSH
margin ratio of 1.1 indicates that NPSHA is 10% greater
than NPSHR.
• As the difference between NPSHA and NPSHR. As a rule
of thumb, it is necessary to ensure that the NPSH
margin is 0.5m or higher (that is: NPSHA =NPSHR +
0.5m).
Net Positive Suction Head
Example 1
A 32-in pump, with actual pump curve shown in the next
slide, is to pump 24,000 gal/min of water at 1170 r/min
from a reservoir whose surface is at 14.7 lbf/in^2
absolute. If head loss from reservoir to pump inlet is 6 ft,
where should the pump inlet be placed to avoid
cavitation for water at 60°F, 𝑃𝑣𝑎𝑝𝑜𝑟 = 0.26 lbf/in^2 abs.,
SG = 1.0.
Example 2
For the pump setting shown below, water at 25°C is
pumped at 19,000 gpm by a 38-in centrifugal pump
running at 710 rpm whose pump curve is shown in the
next slide. The head losses in the suction pipe is 3.8 ft.
The atmospheric pressure is measured to be 14.7 psia.