i

UNIT IV. CENTROIDS, CENTERS OF GRAVITY, DISTRIBUTED LOADS,

AND MOMENTS OF INERTIA

Overview

In this unit, you will learn about the centroids, centers of gravity, and moments of
inertia of different shapes, figures, and volumes. You will also learn how to solve problems in
statics involving distributed loads.

Learning Objectives:

At the end of this unit, I am able to:

1. Identify the centroids, centers of gravity, and moments of inertia of different shapes
and volumes.
2. Differentiate center of mass and center of gravity.
3. Solve problems in statics involving distributed loads.

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 2

Lesson Proper

CENTER OF MASS AND CENTER OF GRAVITY

The center of mass of an object is the point where the distribution of mass of the object is
equal in all directions, it is not dependent on gravitational field. The center of gravity of an
object is the point where the distribution of weight of the object is equal in all directions and
it is dependent on gravitational field. This is the point where the weight of the object tends to
act.

The object on the left is under a uniform gravitational field and has coinciding centers of mass
and gravity. The gravitational field for the object on the right is stronger on the bottom and
gets weaker as it gets higher. In this case, the center of gravity is below the center of mass of
an object.

In most cases, the center of mass and center of gravity will coincide, since the gravitational
field on earth is fairly uniform, thus, they can be used interchangeably.

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 3

CENTROIDS

The centroid is the geometric center of a plane figure. It is the average position of all point
within the figure.

Centroids of Common Geometric Shapes

Centroid
Shape Area
x̄ ȳ

𝟏 𝟏
𝑨 = 𝒃𝒅 𝒙= 𝒃 𝒚= 𝒅
𝟐 𝟐

𝟏 𝟏
𝑨= 𝒃𝒉 𝒚= 𝒉
𝟐 𝟑

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 4

𝑨 = 𝝅𝒓𝟐 𝒙=𝟎 𝒚=𝟎

𝟏 𝟐 𝟒𝒓
𝑨= 𝝅𝒓 𝒙=𝟎 𝒚=
𝟐 𝟑𝝅

𝟐𝒓
𝑳 = 𝝅𝒓 𝒙= 𝒚=𝟎
𝝅

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 5

𝟏 𝟐 𝟒𝒓 𝟒𝒓
𝑨= 𝝅𝒓 𝒙= 𝒚=
𝟒 𝟑𝝅 𝟑𝝅

𝟐𝒓𝒔𝒊𝒏𝜽
𝑨 = 𝒓𝟐 𝜽𝒓𝒂𝒅 𝒙= 𝒚=𝟎
𝟑𝜽𝒓𝒂𝒅

𝒓𝒔𝒊𝒏𝜽
𝑳 = 𝟐𝒓𝜽𝒓𝒂𝒅 𝒙= 𝒚=𝟎
𝜽𝒓𝒂𝒅

𝑨 = 𝝅𝒂𝒃 𝒙=𝟎 𝒚=𝟎

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 6

𝟏 𝟒𝒃
𝑨= 𝝅𝒂𝒃 𝒙=𝟎 𝒚=
𝟐 𝟑𝝅

𝟏 𝟒𝒂 𝟒𝒃
𝑨= 𝝅𝒂𝒃 𝒙= 𝒚=
𝟒 𝟑𝝅 𝟑𝝅

𝟐 𝟑 𝟐
𝑨= 𝒃𝒉 𝒙= 𝒃 𝒚= 𝒉
𝟑 𝟖 𝟓

𝟏 𝟏 𝒏+𝟏
𝑨= 𝒃𝒉 𝒙= 𝒃 𝒚= 𝒉
𝒏+𝟏 𝒏+𝟐 𝟒𝒏 + 𝟐

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 7

Centroid of a Composite Area

𝐴𝑥 = ∑ 𝑎𝑥

𝐴𝑦 = ∑ 𝑎𝑦

Where:

A = total area of the figure

x̄ = x-coordinate of the centroid

∑ax = sum of the products of areas and x-coordinates of the parts of the figure

ȳ = y-coordinate of the centroid

∑ay = sum of the products of areas and y-coordinates of the parts of the figure

Center of gravity of a homogeneous flat plate

𝑊𝑥 = ∑ 𝑤𝑥

𝑊𝑦 = ∑ 𝑤𝑦

Where:

W= total weight of the object

x̄ = x-coordinate of the center of gravity

∑wx = sum of the products of areas and x-coordinates of the parts of the object

ȳ = y-coordinate of the center of gravity

∑wy = sum of the products of areas and y-coordinates of the parts of the object

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 8

Centroids of Lines

𝐿𝑥 = ∑ 𝑙𝑥

𝐿𝑦 = ∑ 𝑙𝑦

L = total length of the line

x̄ = x-coordinate of the centroid

∑lx = sum of the products of length and x-coordinates of the parts of the line

ȳ = y-coordinate of the centroid

∑ly = sum of the products of length and y-coordinates of the parts of the line

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 9

Center of gravity of bodies

𝑊𝑥 = ∑ 𝑤𝑥

𝑊𝑦 = ∑ 𝑤𝑦

𝑊𝑧 = ∑ 𝑤𝑧

Where:

W= total weight of the object

x̄ = x-coordinate of the center of gravity

∑wx = sum of the products of weight and x-coordinates of the parts of the object

ȳ = y-coordinate of the center of gravity

∑wy = sum of the products of weight and y-coordinates of the parts of the object

𝑧 = z-coordinate of the center of gravity

∑wz = sum of the products of weight and z-coordinates of the parts of the object

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 10

Centroid of Volumes

𝑉𝑥 = ∑ 𝑣𝑥

𝑉𝑦 = ∑ 𝑣𝑦

𝑉𝑧 = ∑ 𝑣𝑧

Where:

V= total volume of the object

x̄ = x-coordinate of the centroid

∑vx = sum of the products of volume and x-coordinates of the parts of the object

ȳ = y-coordinate of the centroid

∑vy = sum of the products of volume and y-coordinates of the parts of the object

𝑧 = z-coordinate of the centroid

∑vz = sum of the products of volume and z-coordinates of the parts of the object

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 11

Example 1

a. Determine the distance of the centroid of the T-section of a cast iron beam from its
base.
b. What should be the width of the flange so that the centroid of the T-section is 2.5 in
above the base?

Solution

Divide the figure into common shapes.

a. Identify the areas and their respective

centroids.

𝐴1 = 𝑏ℎ = (6 𝑖𝑛)(1 𝑖𝑛) = 6 𝑖𝑛2

1 1
𝑦1 = (ℎ) = (1 𝑖𝑛)
2 2

𝑦1 = 0.5 𝑖𝑛 (from the base of the T-section)

𝐴2 = 𝑏ℎ = (1 𝑖𝑛)(8 𝑖𝑛) = 8 𝑖𝑛2

1 1
𝑦2 = (ℎ) = (8 𝑖𝑛)
2 2

𝑦2 = 4 𝑖𝑛 (from the bottom of the rectangle)

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 12

𝑦2 = 5 𝑖𝑛 (from the base of the T-section)

𝐴 = 𝐴1 + 𝐴2 = 6 𝑖𝑛2 + 8 𝑖𝑛2

𝐴 = 14 𝑖𝑛2

𝐴𝑦 = ∑ 𝑎𝑦

𝐴𝑦 = 𝐴1 𝑦1 + 𝐴2 𝑦2

(14 𝑖𝑛2 )𝑦 = (6 𝑖𝑛2 )(0.5 𝑖𝑛) + (8 𝑖𝑛2 )(5 𝑖𝑛)

(14 𝑖𝑛2 )𝑦 = 43 𝑖𝑛3

𝒚 = 𝟑. 𝟎𝟕 𝒊𝒏 (𝒇𝒓𝒐𝒎 𝒕𝒉𝒆 𝒃𝒂𝒔𝒆)

b. To lower the centroid of the T-section to 2.5 in above the base, the width of the
flange should be increased.

𝑦 = 2.5 𝑖𝑛

𝐴1 = 𝑏ℎ = (𝑓)(1 𝑖𝑛) = 𝑓 𝑖𝑛2

𝑦1 = 0.5 𝑖𝑛 (above the base of the T-section)

𝐴2 = 8 𝑖𝑛2

𝑦2 = 5 𝑖𝑛 (above the base of the T-section)

𝐴 = 𝐴1 + 𝐴2 = 𝑓 + 8 𝑖𝑛2

𝐴𝑦 = ∑ 𝑎𝑦

𝐴𝑦 = 𝐴1 𝑦1 + 𝐴2 𝑦2

(𝑓 + 8)(2.5) = (𝑓)(0.5 ) + (8)(5)

2.5𝑓 + 20 = 0.5𝑓 + 40

2𝑓 = 20

𝒇 = 𝟏𝟎 𝒊𝒏

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 13

Example 2

Locate the centroid of the shaded area formed by cutting a semicircle with diameter r from
a quarter circle with radius r.

Solution

For the quarter circle

1
𝐴1 = 𝜋𝑟 2
4
4𝑟
𝑥1 =
3𝜋
4𝑟
𝑦1 =
3𝜋

For the semicircle

1 1 1
𝐴2 = ( 𝜋𝑑2 ) = 𝜋𝑟 2
2 4 8
1
4(2 𝑟) 2𝑟
𝑥1 = =
3𝜋 3𝜋
1
𝑦1 = 𝑟
2

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 14

For the shaded area

𝑨 = 𝑨𝟏 − 𝑨𝟐

𝟏 𝟐 𝟏 𝟐
𝑨= 𝝅𝒓 − 𝝅𝒓
𝟒 𝟖
𝟏 𝟐
𝑨= 𝝅𝒓
𝟖

𝐴𝑥 = ∑ 𝑎𝑥

𝐴𝑥 = 𝐴1 𝑥1 + 𝐴2 𝑥2

1 1 4𝑟 1 2𝑟
( 𝜋𝑟 2 ) 𝑥 = ( 𝜋𝑟 2 ) ( ) − ( 𝜋𝑟 2 ) ( )
8 4 3𝜋 8 3𝜋
1 1 1
( 𝜋𝑟 2 ) 𝑥 = 𝑟 3 − 𝑟 3
8 3 12
1 1
( 𝜋𝑟 2 ) 𝑥 = 𝑟 3
8 4
1 3
𝑟
𝑥= 4
1 2
𝜋𝑟
8
𝟐𝒓
𝒙= = 𝟎. 𝟔𝟑𝟔𝟔𝒓
𝝅

𝐴𝑦 = ∑ 𝑎𝑦

𝐴𝑦 = 𝐴1 𝑦1 + 𝐴2 𝑦2

1 1 4𝑟 1 1
( 𝜋𝑟 2 ) 𝑦 = ( 𝜋𝑟 2 ) ( ) − ( 𝜋𝑟 2 ) ( 𝑟)
8 4 3𝜋 8 2
1 1 1
( 𝜋𝑟 2 ) 𝑦 = 𝑟 3 − 𝜋𝑟 3
8 3 16
1 1 1
( 𝜋𝑟 2 ) 𝑦 = ( − 𝜋) 𝑟 3
8 3 16
𝟏 𝟏
(𝟑 − 𝟏𝟔 𝝅) 𝒓𝟑
𝒚= = 𝟎. 𝟑𝟒𝟖𝟖𝒓
𝟏
(𝟖 𝝅) 𝒓𝟐

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 15

Centroids determined by integration

Centroid of area
𝑏
𝐴𝑥 = ∫ 𝑥𝑐 𝑑𝐴
𝑎

𝑏
𝐴𝑦 = ∫ 𝑦𝑐 𝑑𝐴
𝑎

Where:

A = total area of the figure

x̄ = x-coordinate of the centroid

xc = x-coordinate of the centroid of the differential strip

ȳ = y-coordinate of the centroid

yc = y-coordinate of the centroid of the differential strip

Center of gravity of bodies

𝑏
𝑊𝑥 = ∫ 𝑥𝑐 𝑑𝑊
𝑎

𝑏
𝑊𝑦 = ∫ 𝑦𝑐 𝑑𝑊
𝑎

𝑏
𝑊𝑧 = ∫ 𝑧𝑐 𝑑𝑊
𝑎

Center of gravity of bodies

𝑏
𝑉𝑥 = ∫ 𝑥𝑐 𝑑𝑉
𝑎

𝑏
𝑉𝑦 = ∫ 𝑦𝑐 𝑑𝑉
𝑎

𝑏
𝑉𝑧 = ∫ 𝑧𝑐 𝑑𝑉
𝑎

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 16

Example 3

Determine the centroid of the triangular area bounded by the x-axis, the line x = a, and the
line y=kx.

Solution:

Find the value of k

At point (a, b)

𝒚 = 𝒌𝒙

𝒃 = 𝒌𝒂

𝒃
𝒌=
𝒂

Thus,

𝒃
𝒚= 𝒙
𝒂

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 17

Differential area,

𝒅𝑨 = 𝒚𝒅𝒙

𝒃
𝒅𝑨 = ( 𝒙) 𝒅𝒙
𝒂
Area of the shaded region under the parabola by integration,
𝑎
𝒃
𝐴 = ∫ ( 𝒙) 𝒅𝒙
0 𝒂

𝒃 𝑎
𝐴 = ∫ 𝒙𝒅𝒙
𝒂 0
𝑎
𝒃 𝑥2
𝐴= [ ]
𝒂 2 0

𝑏 2
𝐴= [𝑎 − 02 ]
2𝑎
1
𝐴 = 𝑎𝑏
2
Distance of centroid from the y-axis (x-coordinate of the centroid)
𝑏
𝐴𝑥 = ∫ 𝑥𝑐 𝑑𝐴
𝑎

𝑎
1 𝑏
𝑎𝑏𝑥 = ∫ 𝑥 ( 𝑥) 𝑑𝑥
2 0 𝑎

1 𝑏 𝑏 2
𝑎𝑏𝑥 = ∫ 𝑥 𝑑𝑥
2 𝑎 𝑎
𝑎
1 𝑏 𝑥3
𝑎𝑏𝑥 = [ ]
2 𝑎 3 0

1 𝑏 3
𝑎𝑏𝑥 = [𝑎 − 03 ]
2 3𝑎

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 18

1 1
𝑎𝑏𝑥 = 𝑎2 𝑏
2 3
𝟐
𝒙= 𝒂
𝟑
Distance of centroid from the x-axis (y-coordinate of the centroid)
𝑏
𝐴𝑦 = ∫ 𝑦𝑐 𝑑𝐴
𝑎

𝑎
1 1
𝑎𝑏𝑦 = ∫ 𝑦 (𝑦𝑑𝑥)
2 0 2

1 1 𝑏 2
𝑎𝑏𝑦 = ∫ 𝑦 𝑑𝑥
2 2 𝑎

1 1 𝑏 𝑏 2
𝑎𝑏𝑦 = ∫ ( 𝑥) 𝑑𝑥
2 2 𝑎 𝑎

1 𝑏2 𝑏 2
𝑎𝑏𝑦 = 2 ∫ 𝑥 𝑑𝑥
2 2𝑎 𝑎
𝑎
1 𝑏2 𝑥 3
𝑎𝑏𝑦 = 2 [ ]
2 2𝑎 3 0

1 𝑏2 3
𝑎𝑏𝑦 = 2 [𝑎 − 03 ]
2 6𝑎
1 1
𝑎𝑏𝑦 = 𝑎𝑏 2
2 6
𝟏
𝒚= 𝒃
𝟑

𝟐 𝟏
The location of the centroid is at point ( 𝒂 , 𝒃).
𝟑 𝟑

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 19

DISTRIBUTED LOADS

Distributed loads are loads that are applied over a specified area, unlike concentrated loads
which are loads that are applied on a single point.

Distributed loads Concentrated loads

A distributed load can be simplified by converting it into a concentrated load. The equivalent
concentrated load will be equal to the magnitude of the area of the distributed load.

For example, the area of the uniformly distributed with a magnitude of 100 lb/ft over a length
𝑙𝑏
of 10 ft will be equal to a concentrated load of magnitude (100 𝑓𝑡
) (10 𝑓𝑡) = 1000 𝑓𝑡.

The location of the equivalent concentrated load will be at the centroid of the area of the
distributed load.

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 20

Example 4

Determine the reactions R1 and R2 of the beam below loaded with a

concentrated load of 1600 lb and a uniformly varying distributed load
from zero to an intensity of 400 lb/ft.

Solution:

Convert the distributed load into a concentrated load.

1 𝑙𝑏
𝑃 = (400 ) (12 𝑓𝑡)
2 𝑓𝑡

𝑃 = 2400 𝑙𝑏

Find the centroid of the distributed load along the x-axis.

1 1
𝑥 = 𝑏 = (12 𝑓𝑡)
3 3
𝑥 = 4 𝑓𝑡 (from the right)

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 21

2400 lb

For the upper beam,

∑ 𝑴𝑹 𝟑 = 𝟎

𝟐𝟒𝟎𝟎 𝒍𝒃(𝟖 𝒇𝒕) = 𝑹𝟒 (𝟏𝟐 𝒇𝒕)

𝑹𝟒 = 𝟏𝟔𝟎𝟎 𝒍𝒃

∑ 𝑭𝒚 = 𝟎

𝑹𝟑 + 𝑹𝟒 = 𝟐𝟒𝟎𝟎 𝒍𝒃

𝑹𝟑 + 𝟏𝟔𝟎𝟎 𝒍𝒃 = 𝟐𝟒𝟎𝟎 𝒍𝒃

𝑹𝟑 = 𝟖𝟎𝟎 𝒍𝒃

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 22

For the lower beam,

∑ 𝑴𝑹 𝟏 = 𝟎

(𝟏𝟔𝟎𝟎 𝒍𝒃)(𝟑 𝒇𝒕) + (𝑹𝟑 )(𝟒 𝒇𝒕) + (𝑹𝟒 )(𝟏𝟔 𝒇𝒕) = (𝑹𝟐 )(𝟏𝟔 𝒇𝒕)

(𝟏𝟔𝟎𝟎 𝒍𝒃)(𝟑 𝒇𝒕) + (𝟖𝟎𝟎)(𝟒 𝒇𝒕) + (𝟏𝟔𝟎𝟎)(𝟏𝟔 𝒇𝒕) = (𝑹𝟐 )(𝟏𝟔 𝒇𝒕)

𝑹𝟐 = 𝟐𝟏𝟎𝟎 𝒍𝒃

∑ 𝑭𝒚 = 𝟎

𝑹𝟏 + 𝑹𝟐 = 𝟏𝟔𝟎𝟎 𝒍𝒃 + 𝑹𝟑 + 𝑹𝟒

𝑹𝟏 + 𝟐𝟏𝟎𝟎 𝒍𝒃 = 𝟏𝟔𝟎𝟎 𝒍𝒃 + 𝟖𝟎𝟎 𝒍𝒃 + 𝟏𝟔𝟎𝟎 𝒍𝒃

𝑹𝟏 = 𝟏𝟗𝟎𝟎 𝒍𝒃

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 23

Example 5

The billboard BC weighing 1000 lb is subjected to a wind pressure of 300 lb/ft as shown in
below. Neglecting the weights of the support-members, determine the components of the
hinge force at F.

Solution:

From the FBD of the whole system

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 24

Convert the uniformly distributed load into a concentrated load.

𝑙𝑏
𝑃 = (300 ) (10 𝑓𝑡)
𝑓𝑡

𝑃 = 3000 𝑙𝑏

Determine the centroid of the distributed load along the y-axis.

1
𝑦 = (10 𝑓𝑡)
2

𝑦 = 5 𝑓𝑡 (𝑎𝑏𝑜𝑣𝑒 𝑝𝑜𝑖𝑛𝑡 𝐵)

3000 lb

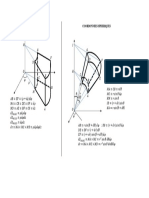
∑ 𝑀𝐴 = 0

𝑃(9 𝑓𝑡) + 𝑊(6 𝑓𝑡) + 𝐹𝐻 (4 𝑓𝑡) = 𝐹𝑉 (12 𝑓𝑡)

(3000 𝑙𝑏)(9 𝑓𝑡) + (1000 𝑙𝑏)(6 𝑓𝑡) + 𝐹𝐻 (4 𝑓𝑡) = 𝐹𝑉 (12 𝑓𝑡)

33000 𝑙𝑏. 𝑓𝑡 + 𝐹𝐻 (4 𝑓𝑡) = 𝐹𝑉 (12 𝑓𝑡)

𝟖𝟐𝟓𝟎 𝒍𝒃 + 𝑭𝑯 = 𝟑𝑭𝑽 (eq. 1)

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 25

FBD of member BC

∑ 𝑀𝐵 = 0 3000 lb

(3000 𝑙𝑏)(5 𝑓𝑡) = 𝐶𝐻 (10 𝑓𝑡)

𝐶𝐻 = 1500 𝑙𝑏

FBD of member CD

∑ 𝐹𝐻 = 0

𝐷𝐻 = 𝐶𝐻

𝐷𝐻 = 1500 𝑙𝑏

FBD of member DF

∑ 𝑀𝐸 = 0

𝐷𝐻 (4 𝑓𝑡) = 𝐹𝐻 (4 𝑓𝑡)

𝐹𝐻 = 𝐷𝐻

𝑭𝑯 = 𝟏𝟓𝟎𝟎 𝒍𝒃

Substitute in equation 1

8250 𝑙𝑏 + 𝐹𝐻 = 3𝐹𝑉

8250 𝑙𝑏 + 1500 𝑙𝑏 = 3𝐹𝑉

𝑭𝑽 = 𝟑𝟐𝟓𝟎 𝒍𝒃

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 26

Area Moment of Inertia

The Area Moment of Inertia, also called the Second Moment of Area is the product of an area
and the square of its moment arm about a reference axis. It is used to measure the resistance
to bending of a cross section of an object. The area moment of inertia is used in designing
beams and shafts.

Area moment of inertia about the x-axis

𝐼𝑥 = ∫ 𝑦 2 𝑑𝐴

Area moment of inertia about the x-axis

𝐼𝑦 = ∫ 𝑥 2 𝑑𝐴

Polar Moment of Inertia

Polar moment of inertia is the area moment of inertia about the z-axis, it is equal to the sum
of the moments of inertia about the x and y axes.

𝐽 = 𝐼𝑥 + 𝐼𝑦

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 27

Transfer Formula for Moment of Inertia

𝑰 = 𝑰 + 𝑨𝒅𝟐
Where:
x′ = centroidal axis
x = any axis parallel to the centroidal axis
I = moment of inertia about the x-axis
𝐼 = centroidal moment of inertia
A = area of the section
d = distance between x and x’

Transfer formula for Polar Moment of Inertia

𝐽 = 𝐽 + 𝐴𝑑2
Radius of Gyration
Radius of gyration is the distance from the axis of rotation of an area to the point
where the whole area tends to act.

𝐼
𝑘=√
𝐴

𝐼𝑥
𝑘𝑥 = √
𝐴

𝐼𝑦
𝑘𝑦 = √
𝐴

𝐽
𝑘𝑧 = √
𝐴
Transfer formula for Radius of Gyration

𝑘 2 = 𝑘 2 + 𝑑2

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 28

Moment of Inertia of common shapes

Shape Moment of Inertia Radius of Gyration

𝑏ℎ3
Rectangle 𝐼𝑥 =
12
ℎ𝑏 3
𝐼𝑦 = ℎ
12 𝑘𝑥 =
√12
𝑏ℎ3
𝐼𝑥 = ℎ
3 𝑘=
ℎ𝑏 3 √3
𝐼𝑦 =
3

Triangle
𝑏ℎ3
𝐼𝑥 = ℎ
36 𝑘𝑥 =
√18
𝑏ℎ3
𝐼𝑥 = ℎ
12 𝑘=
√6

Circle

𝜋𝑟 4 𝑟
𝐼𝑥 = 𝑘𝑥 =
4 2

𝜋𝑟 4 𝑟
𝐽= 𝑘=
2 √2

𝜋𝑟 4
𝐼𝑥 = 𝐼𝑦 = 𝑟
8 𝑘𝑥 = 𝑘𝑦 =
2
Semicircle
𝐼𝑥 = 0.11𝑟 4
𝑘𝑥 = 0.264𝑟

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 29

Quarter circle

𝜋𝑟 4 𝑟
𝐼𝑥 = 𝐼𝑦 = 𝑘𝑥 = 𝑘𝑦 =
16 2

𝐼𝑥 = 𝐼𝑦 = 0.055𝑟 4
𝑘𝑥 = 𝑘𝑦 = 0.264𝑟

Ellipse
𝜋𝑎𝑏 3 𝑏
𝐼𝑥 = 𝑘𝑥 =
4 2

𝜋𝑎3 𝑏 𝑎
𝐼𝑦 = 𝑘𝑦 =
4 2

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 30

Example 1
Determine the radius of gyration of a rectangle with dimensions 3 in by 6 in with respect to a
polar axis through one corner.

Solution:

Finding the moment of inertia about the x-axis:

𝑏ℎ3 6(33 )
𝐼𝑥 = =
3 3
𝟒
𝑰𝒙 = 𝟓𝟒 𝒊𝒏
Moment of inertia about the y-axis:
ℎ𝑏 3 3(63 )
𝐼𝑦 = =
3 3
𝑰𝒚 = 𝟐𝟏𝟔 𝒊𝒏𝟒
Polar moment of inertia about the corner:
𝐽 = 𝐼𝑥 + 𝐼𝑦 = 54 + 216
𝑱 = 𝟐𝟕𝟎 𝒊𝒏𝟒
Radius of gyration about the corner

𝐽 270 𝑖𝑛4
𝑘𝑧 = √ = √
𝐴 (3 𝑖𝑛)(6 𝑖𝑛)
𝒌𝒛 = 𝟑. 𝟖𝟕𝟑 𝒊𝒏

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 31

Alternative solution:

Taking the centroidal moment of inertia:

𝑏ℎ3 6(33 )
𝐼𝑥 = = = 13.5 𝑖𝑛4
12 12

ℎ𝑏 3 3(63 )
𝐼𝑦 = = = 54 𝑖𝑛4
12 12

Centroidal polar moment of inertia:

𝐽 = 𝐼𝑥 + 𝐼𝑦 = 13.5 + 54

𝑱 = 𝟔𝟕. 𝟓 𝒊𝒏𝟒

Centroidal radius of gyration:

𝐽 67.5 𝑖𝑛4
𝑘=√ =√ = 1.9365 𝑖𝑛
𝐴 (3 𝑖𝑛)(6 𝑖𝑛)

Using the transfer formula to solve for the radius of gyration about the corner:

ℎ 2 𝑏 2
𝑑2 = ( ) + ( ) = 1.52 + 32 = 11.25 𝑖𝑛2
2 2

𝑘𝑧2 = 𝑘 2 + 𝑑2 = (1.9365 𝑖𝑛)2 + 11.25 𝑖𝑛2

𝑘𝑧2 = 15 𝑖𝑛2

𝒌𝒛 = 𝟑. 𝟖𝟕𝟑 𝒊𝒏

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 32

Type equation here.

Example 2

Determine the centroidal moment of inertia of the area shown below.

Solution:

For Area 1

𝐴1 = (12 𝑖𝑛)(1 𝑖𝑛) = 12 𝑖𝑛2

1 1
𝑦1 = ℎ = (1 𝑖𝑛) = 0.5 𝑖𝑛
2 2

𝑏ℎ3 12(13 )
𝐼1𝑥 = = = 1 𝑖𝑛4
12 12

ℎ𝑏 3 1(123 )
𝐼1𝑦 = = = 144 𝑖𝑛4
12 12

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 33

For Area 2,

𝐴2 = (1 𝑖𝑛)(12 𝑖𝑛) = 12 𝑖𝑛2

1 1
𝑦2 = ℎ + 1 = (12 𝑖𝑛) + 1 = 7 𝑖𝑛
2 2

𝑏ℎ3 1(123 )
𝐼2𝑥 = = = 144 𝑖𝑛4
12 12

ℎ𝑏 3 12(13 )
𝐼2𝑦 = = = 1 𝑖𝑛4
12 12

For Area 3,

𝐴3 = (6 𝑖𝑛)(1 𝑖𝑛) = 6 𝑖𝑛2

1 1
𝑦3 = ℎ + 13 = (1 𝑖𝑛) + 13 = 13.5 𝑖𝑛
2 2

𝑏ℎ3 6(13 )
𝐼3𝑥 = = = 0.5 𝑖𝑛4
12 12

ℎ𝑏 3 1(63 )
𝐼3𝑦 = = = 18 𝑖𝑛4
12 12
Solving for the centroid of the whole area:

𝐴𝑦 = 𝐴1 𝑦1 + 𝐴2 𝑦2 + 𝐴3 𝑦3

(30 𝑖𝑛)𝑦 = (12 𝑖𝑛2 )(0.5 𝑖𝑛) + (12 𝑖𝑛2 )(7 𝑖𝑛) + (6 𝑖𝑛2 )(13.5 𝑖𝑛)

𝑦 = 5.7 𝑖𝑛

Solving for the moment of inertia of the whole area about the centroidal x-axis:

𝐼𝑥 = (𝐼1𝑥 + 𝐴1 𝑑12 ) + (𝐼2𝑥 + 𝐴2 𝑑22 ) + (𝐼3𝑥 + 𝐴3 𝑑32 )

𝐼𝑥 = [𝐼1𝑥 + 𝐴1 (𝑦 − 0.5)2 ] + [𝐼2𝑥 + 𝐴2 (7 − 𝑦)2 ] + [𝐼3𝑥 + 𝐴3 (13.5 − 𝑦)2 ]

𝐼𝑥 = [1 + 12(5.7 − 0.5)2 ] + [144 + 12(7 − 5.7)2 ] + [0.5 + 6(13.5 − 5.7)2 ]

𝑰𝒙 = 𝟖𝟓𝟓. 𝟑 𝒊𝒏𝟒

Solving for the moment of inertia of the whole area about the centroidal y-axis:

𝐼𝑦 = 𝐼1𝑦 + 𝐼2𝑦 + 𝐼3𝑦 = 144 + 1 + 18

𝐼𝑦 = 𝟏𝟔𝟑 𝒊𝒏𝟒

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 34

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads

 35

REFERENCES
Analysis of Structures. (n.d.). Retrieved from Mathalino:
https://mathalino.com/reviewer/engineering-mechanics/analysis-structures

Singer, F. L. (1975). Engineering Mechanics Statics and Dynamics (Third ed.). New York: Harper &
Row.

Centroids, Centers of Gravity, Moments Of Inertia, and Distributed Loads