Derivatives as the Slope of Tangent Line Week 7

Content Standards

The learners demonstrate an understanding of basic concepts of derivatives.

Performance Standards

The learner shall be able to formulate and solve accurately situational problems involving extreme
values.

Most Essential Learning Competencies

At the end of the lesson, you should be able to:

1. Illustrate the tangent line to the graph of a function at a given point;

2. Applies the definition of the derivative of a function at a given number; and
3. Relate the derivative of a function to the slope of the tangent line.

Lesson Presentation
Terminologies

✓ Tangent Line - a line that locally touches a curve at one and only one point.
✓ Slope-intercept formula - The slope-intercept formula for a line is y = mx + b, where m is the slope of
the line and b is the y-intercept.
✓ Point-slope formula - The point-slope formula for a line is y – y1 = m (x – x1). This formula uses a point
on the line, denoted by (x1, y1), and the slope of the line, denoted by m, to calculate the slope-intercept
formula for the line.

Basic Calculus Page 1 of 17

Derivatives as the Slope of Tangent Line Week 7

Discussion

In this lesson, we are going to look at important problems in the study of calculus. It will lead us to the study of
limits, which is the topic of this chapter after all. Looking at these problems here will allow us to start to
understand just what a limit is and what it can tell us about a function.

Finding the Equation of a Tangent Line

For certain problems in Calculus, I call for using the first derivative to find the equation of the tangent line to a
curve at a specific point.

The following diagram illustrates these problems.

There are certain things you must

remember when solving for the equation
of a tangent line:

1. A Tangent Line is a line that locally

touches a curve at one and only one point.

2. The slope-intercept formula for a line is

𝑦 = 𝑚𝑥 + 𝑏, where m is the slope of the
line and b is the y-intercept.

3. The point-slope formula for a line is 𝑦 – 𝑦1 = 𝑚 (𝑥 – 𝑥1 ). This formula uses a point on the line, denoted by
(𝑥1 , 𝑦1 ), and the slope of the line, denoted by m, to calculate the slope-intercept formula for the line.

Also, there is some information from Calculus you must use:

1. The first derivative is an equation for the slope of a tangent line to a curve at an indicated point.
2. The first derivative may be found using:

Basic Calculus Page 2 of 17

Derivatives as the Slope of Tangent Line Week 7

a. The definition of a derivative.

𝒇(𝒙 + 𝒉) − 𝒇(𝒙)
𝐥𝐢𝐦
𝒉→𝟎 𝒉

b. Methods are already known to you for derivation, such as:

• Power Rule
• Product Rule
• Quotient Rule
• Chain Rule

With these formulas and definitions in mind, you can find the equation of a tangent line.

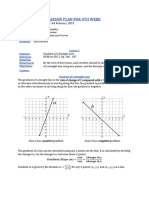
Example 1: Find the equation of the line tangent to 𝑓 (𝑥) = 𝑥 2 at 𝑥 = 2. Having a graph is helpful when
trying to visualize the tangent line. Therefore, consider the following graph of the problem:

The equation for the slope of the tangent line to

𝑓 (𝑥) = 𝑥 2 is 𝑓 ′(𝑥), the derivative of 𝑓(𝑥). Using the
power rule yields the following:

𝑓 (𝑥) = 𝑥 2

𝑓 ′(𝑥) = 2𝑥

Therefore, at 𝑥 = 2, the slope of the tangent line is

𝑓 ′(2). 𝑓 ′(2) = 2(2) = 4

Now, you know the slope of the tangent line, which is 4. All that you need now is a point on the tangent line to
be able to formulate the equation.

Basic Calculus Page 2 of 17

Derivatives as the Slope of Tangent Line Week 7

You know that the tangent line shares at least one point with the original equation, 𝑓(𝑥) = 𝑥2. Since the line
you are looking for is tangent to 𝑓(𝑥) = 𝑥 2 at 𝑥 = 2, you know the 𝑥 coordinate for one of the points on the
tangent line. By plugging the 𝑥 coordinate of the shared point into the original equation you have:

𝑓(𝑥) = 22 = 4 𝑜𝑟 𝑦 = 4

Therefore, you have found the coordinates, (2, 4), for the point shared by 𝑓(𝑥) and the line tangent to 𝑓(𝑥) at
𝑥 = 2. Now you have a point on the tangent line and the slope of the tangent line from step (1).

The only step left is to use the point (2, 4) and slope, 4, in the point-slope formula for a line. Therefore,

𝑦 − 𝑦1 = 𝑚(𝑥 − 𝑥1 )

𝑦 − 4 = 4(𝑥 − 2)

𝑦 − 4 = 4𝑥 − 4

𝑦 = 4𝑥 − 4

This is the equation for the tangent line 𝑦 = 4𝑥 – 4

Finally, check with the graph to see if your answer is reasonable.

Basic Calculus Page 3 of 17

Derivatives as the Slope of Tangent Line Week 7

The tangent line appears to have a slope of 4 and a y-intercept at –4, therefore the answer is quite reasonable.
Therefore, the line 𝑦 = 4𝑥– 4 is tangent to 𝑓(𝑥) = 𝑥2at𝑥 = 2.

Example 2: Finding the equation of the line tangent to the graph of 𝑓(𝑥) = 𝑥2at 𝑥 = 3?This is the formal
definition for the derivative of function f at the point 𝑥 = 𝑐:

𝒇(𝒄 + 𝒉) − 𝒇(𝒄)
𝐥𝐢𝐦
𝒉→𝟎 𝒉

It represents the limit of a sequence of slopes of secant lines that approach the tangent line at 𝑥 = 𝑐.All
weneedtodonow isplug𝑥 = 3 and𝑓(𝑥) = 𝑥2:

Step1:What'sanexpressionforthederivative of𝑓(𝑥) = 𝑥2at𝑥 = 3?

𝑓(3 + ℎ) − 𝑓(3)
𝑓 ′ (3) = lim
ℎ→0 ℎ

′ (3)
𝑓(3 + ℎ)2 − 𝑓(3)2
𝑓 = lim
ℎ→0 ℎ

Step 2: Evaluate the correct limit from the previous step.

𝑓(3 + ℎ)2 − 𝑓(3)2

𝑓 ′ (3) = lim
ℎ→0 ℎ

9 + 6ℎ + ℎ2 − 9
𝑓 ′ (3) = lim
ℎ→0 ℎ

ℎ(6 + ℎ)
= lim
ℎ→0 ℎ

= lim 6 + ℎ
ℎ→0

=6

Basic Calculus Page 4 of 17

Derivatives as the Slope of Tangent Line Week 7

𝑓′ (3) 𝑓, prime, left parenthesis, 3, right parenthesis gives us the slope of the tangent line. To find the
complete equation, we need a point the line goes through.

Usually, that point will be the point where the tangent line touches the graph of f.

Step 3: What is the point we should use for the equation of the line?

The intersection point is the point on the graph of f where 𝑥 = 3:

𝑓(3) = (3)2 = 9

Step 4: Complete the equation of the line tangent to the graph of 𝑓(𝑥) = 𝑥 2 at 𝑥 = 3

We are looking for the equation of the line whose slope is 6 and that goes through that point (3,9).

To do that, we can use the definition of slope: 6 = 𝑦 − 9 𝑥 − 3

Using the definition of the derivative, we were able to find the equation for the line tangent to the graph of
𝑓(𝑥) = 𝑥 2 at 𝑥 = 3

Now we can isolate y:

𝑦−9
6=
𝑥−3

6(𝑥 − 3) = 𝑦 − 9

6(𝑥 − 3) + 9 = 𝑦

Therefore, the equation of the line is𝑦 = 6(𝑥 − 3) + 9

Example 3: Finding the equation of the line tangent to 𝑓(𝑥) = 𝑥 2 + 3 at 𝑥 = −5. We plug 𝑥 = −5 and
𝑓(𝑥) = 𝑥 2 + 3 in the definition for the derivative:

Basic Calculus Page 5 of 17

Derivatives as the Slope of Tangent Line Week 7

′ (−5)
𝑓(−5 + ℎ)2 − 𝑓(−5)2
𝑓 = lim
ℎ→0 ℎ
[(−5 + ℎ)2 + 3] − [(−5)2 + 3]
= lim
ℎ→0 ℎ
[25 − 10 + ℎ2 + 3] − [25 + 3]
= lim
ℎ→0 ℎ
ℎ2 − 10ℎ
= lim
ℎ→0 ℎ
= lim ℎ − 10
ℎ→0

= −10

So, the slope of the tangent line is -10. Now we need a point on the line: 𝑓 (−5) = (−5)2 + 3 = 28

So we are looking for the equation of the line whose slope is -10 and that goes through the point (-5, 28).

𝑦 − (28)
−10 =
𝑥 − (−5)

𝑦 − 28
−10 =
𝑥+5

−10(𝑥 + 5) = 𝑦 − 28

−10(𝑥 + 5) + 28 = 𝑦

Therefore, the equation of the line is 𝑦 = −10 (𝑥 + 5) + 28.

Terminologies

✓ Differentiation rules - allow us to compute the derivatives of such functions without using the formal
definition of the derivative.

Basic Calculus Page 6 of 17

Derivatives as the Slope of Tangent Line Week 7

✓ Exponential Function - a function whose value is a constant raised to the power of the argument,
especially the function where the constant is e.
✓ Trigonometric function - a function of an angle, or of an abstract quantity, used in trigonometry,
including the sine, cosine, tangent, cotangent, secant, and cosecant, and their hyperbolic counterparts.
✓ Power rule - is a quick tool for finding the derivative of a function.
✓ Constant multiple rule - The Constant multiple rules says the derivative of a constant multiplied by a
function is the constant multiplied by the derivative of the function. The Constant rule says the
derivative of any constant function is always 0.

Rules of Differentiation

It is tedious to compute a limit every time we need to know the derivative of a function. Fortunately, we can
develop a small collection of examples and rules that allow us to quickly compute the derivative of almost any
function we are likely to encounter.

We’ve learned that to find the rule for the derivative f ′of a function f, we first find the difference quotient.

𝑓(𝑥 + ℎ) − 𝑓(𝑥)
lim
ℎ→0 ℎ

But this method is tedious and time consuming, even for relatively simple functions. This chapter we will
develop rules that will simplify the process of finding the derivative of a function.

Basic Rules of Differentiation

Rule 1: Derivative of a Constant

𝑑
We will use the notation 𝑑𝑥 [𝑓(𝑥)]to mean “the derivative of f with respect to 𝑥 at 𝑥.”

Basic Calculus Page 7 of 17

Derivatives as the Slope of Tangent Line Week 7

𝒅
(𝒄) = 𝟎
𝒅𝒙

The derivative of a constant function is equal to zero.

- We can see geometrically why the derivative of a constant must be zero.

- The graph of a constant function is a straight line parallel to the x axis.
- Such a line has a slope that is constant with a value of zero.
- Thus, the derivative of a constant must be zero as well.

𝑓(𝑥) = 𝑐

We can use the definition of the derivative to

demonstrate this:

𝑓(𝑥 + ℎ) − 𝑓(𝑥)
𝑓 ′ (𝑥) = lim
ℎ→𝑜 ℎ

𝑐−𝑐
= lim
ℎ→0 ℎ

= lim
ℎ→0

=0

Rule 2: The Power Rule

𝑑
If n is any real number, then 𝑑𝑥 (𝑥)𝑛 = 𝑛𝑥 𝑛−1

Let’s verify this rule for the special case of 𝑛 = 2.

If 𝑓(𝑥) = 𝑥 2 , then

𝑑 2 𝑓(𝑥 + ℎ) − 𝑓(𝑥)
𝑓 ′ (𝑥) = (𝑥 ) = lim
𝑑𝑥 ℎ→0 ℎ

Basic Calculus Page 8 of 17

Derivatives as the Slope of Tangent Line Week 7

(𝑥 + ℎ)2 − 𝑥 2 𝑥 2 + 2𝑥ℎ + ℎ2 − 𝑥 2
= lim = lim
ℎ→0 ℎ ℎ→0 ℎ

2𝑥ℎ + ℎ2 ℎ(2𝑥 + ℎ)
= lim = lim = lim (2𝑥 + ℎ) = 2𝑥
ℎ→0 ℎ ℎ→0 ℎ ℎ→0

Rule 3: Derivative of a Constant Multiple Function

Example1.If𝑓(𝑥) = 𝑥,then Example2.𝑓(𝑥) = 𝑥 8 ,then Example3. 𝑓(𝑥) = 𝑥 5⁄2 then

𝑑 𝑑 8 𝑑 5
𝑓 ′ (𝑥) = (𝑥) = 1 ∙ 𝑥 1−1 𝑓 ′ (𝑥) = (𝑥 ) = 8 ∙ 𝑥 8−1 𝑓 ′ (𝑥) = (𝑥 5⁄2 ) = 𝑥 5⁄2−1
𝑑𝑥 𝑑𝑥 𝑑𝑥 2

= 𝑥0 = 8𝑥 7 5
= 𝑥 3⁄2
2
=1

1
Example4.Findthederivativeof𝑓(𝑥) = √𝑥 Example5.Findthederivativeof𝑓(𝑥) = 3
√𝑥

𝑑 𝑑 1⁄2
𝑓 ′ (𝑥) = (√𝑥) = (𝑥 ) 𝑑 1 𝑑 −1⁄3
𝑑𝑥 𝑑𝑥 𝑓 ′ (𝑥) = (3 ) = 𝑥
𝑑𝑥 √𝑥 𝑑𝑥
1 1
= 𝑥 2 −1 1 1
2 = − 𝑥 −3−1
3
1
= 𝑥 −1⁄2 1
2 = − 𝑥 −4⁄3
3
1
= 1
2√𝑥 =−
3𝑥 4⁄3

Basic Calculus Page 9 of 17

Derivatives as the Slope of Tangent Line Week 7

If c is any constant real number, then

𝒅 𝒅
[𝒄𝒇(𝒙)] = 𝒄 [𝒇(𝒙)]
𝒅𝒙 𝒅𝒙

3
Example1.Find the derivative of 𝑓(𝑥) = 𝑓 ′ (𝑥) = Example 2. Find the derivative of f(x)=5x3
√𝑥
𝑑
(3𝑥 −1⁄2 ) 𝑑
𝑑𝑥
𝑓 ′ (𝑥) = (5𝑥 3 )
𝑑𝑥
1 3
= 3 (− 𝑥 −2 )
2

3 𝑑 3
=− =5 (𝑥 )
2𝑥 3⁄2 𝑑𝑥

= 15𝑥 2

Rule 4: The Sum Rule

𝒅 𝒅 𝒅
[𝒇(𝒙) ± 𝒈(𝒙)] = [𝒇(𝒙)] ± [𝒈(𝒙)]
𝒅𝒙 𝒅𝒙 𝒅𝒙

Example 1.Find the derivative of 𝑡2 5

Example 2. Find the derivative of 𝑔(𝑡) = 5
+ 𝑡3
𝑓(𝑥) = 4𝑥 5 + 3𝑥 4 − 8𝑥 2 + 𝑥 + 3
𝑑 𝑡2 5 𝑑 1
𝑑 𝑔′ = ( + 3 ) = ( 𝑡 2 + 5𝑡 −3 )
𝑑𝑡 5 𝑡 𝑑𝑡 5
𝑓 ′ (𝑥) = (4𝑥 5 + 3𝑥 4 − 8𝑥 2 + 𝑥 + 3)
𝑑𝑥
1 𝑑 2 𝑑
𝑑 𝑑 𝑑 𝑑 𝑑 = ∙ (𝑡 ) + 5 (𝑡 −3 )
= 4 (𝑥 5 ) + 3 (𝑥 4 ) − 8 (𝑥 2 ) + (𝑥) + (3) 5 𝑑𝑡 𝑑𝑡
𝑑𝑥 𝑑𝑥 𝑑𝑥 𝑑𝑥 𝑑𝑥
1
= (2𝑡) + 5(−3𝑡 −4 )
= 4(5𝑥4) + 3(4𝑥3 ) − 8(2𝑥) + 1 + 0 5

= 20𝑥4 + 12𝑥3 − 16𝑥 + 1 2𝑡 15 2𝑡 5 − 75

= − =
5 𝑡4 5𝑡 4

Basic Calculus Page 10 of

17
Derivatives as the Slope of Tangent Line Week 7

Rule 5: The Product Rule

The derivative of the product of two differentiable functions is given by

𝒅
[𝒇(𝒙)𝒈(𝒙)] = 𝒇(𝒙)𝒈′ (𝒙) + 𝒈(𝒙)𝒇′(𝒙)
𝒅𝒕

3
Example1.Find the derivative of 𝑓 (𝑥) = 𝑥 (√𝑥 + 1)
Example1.Findthederivativeof

𝑓(𝑥) = (2𝑥 2 − 1)(𝑥 3 + 3) 𝑑 1 1 𝑑

𝑓′(𝑥) = 𝑥 3 (𝑥 2 + 1) + (𝑥 2 + 1) 3𝑥 2
𝑑𝑥 𝑑𝑥
𝑑 3 𝑑
𝑓′(𝑥) = (2𝑥 2 − 1) (𝑥 + 3) + (𝑥 3 + 3) (2𝑥 2 − 1) 1 1 1
𝑑𝑥 𝑑𝑥 = 𝑥 3 ( 𝑥 −2 ) + (𝑥 2 + 1)
2
= (2𝑥2 − 1)(3𝑥2 ) + (𝑥3 + 3)(4𝑥)
1 5⁄2
= 𝑥 + 3𝑥 5⁄2 + 3𝑥 2
= 6𝑥 4 − 3𝑥 2 + 4𝑥 4 + 12𝑥 2

7 5⁄2
= 𝑥(10𝑥 3 − 3𝑥 + 12) = 𝑥 + 3𝑥 2
2

Rule 6: The Quotient Rule

The derivative of the quotient of two differentiable functions is given by

𝒅 𝒇(𝒙) 𝒈(𝒙)𝒇′ (𝒙) − 𝒇(𝒙)𝒈′(𝒙)

[ ]= (𝒈(𝒙) ≠ 𝟎)
𝒅𝒙 𝒈(𝒙) [𝒈(𝒙)]𝟐

Basic Calculus Page 11 of

17
Derivatives as the Slope of Tangent Line Week 7

𝑥
Example 1. Find the derivative of𝑓(𝑥) = 2𝑥−4
𝑥 2 +1
Example1.Find the derivative of 𝑓(𝑥) = 𝑥 2−1
𝑑 𝑑
(2𝑥 − 4) (𝑥) − 𝑥 (2𝑥 − 4)
𝑑𝑥 𝑑𝑥
𝑓 ′ (𝑥) =
(2𝑥 − 4)2 (𝑥 2 − 1)
𝑑
(𝑥 2 + 1) − (𝑥 2 + 1)
𝑑
(𝑥 2 − 1)
′ (𝑥) 𝑑𝑥 𝑑𝑥
𝑓 =
(𝑥 2 − 1)2
(2𝑥 − 4)(1) − 𝑥(2)
=
(2𝑥 − 4)2
(𝑥 2 − 1)(2𝑥) − (𝑥 2 − 1)(2𝑥)
=
(𝑥 2 − 1)2
(2𝑥 − 4)(1) − 𝑥(2)
=
(2𝑥 − 4)2
2𝑥 3 − 2𝑥 − 2𝑥 3 − 2𝑥
=
(𝑥 2 − 1)2
4
=−
(2𝑥 − 4)2
4𝑥
=
(𝑥 2 − 1)2

Rule 7: Derivatives of trigonometric functions

a. 𝐷𝑥 (𝑠𝑖𝑛𝑥) = 𝑐𝑜𝑠𝑥 b. 𝐷𝑥 (𝑐𝑜𝑠𝑥) = −𝑠𝑖𝑛𝑥 c.𝐷𝑥 (𝑡𝑎𝑛𝑥) = 𝑠𝑒𝑐 2 𝑥

d.𝐷𝑥 (𝑐𝑜𝑡𝑥) = −𝑐𝑠𝑐 2 𝑥 e.𝐷𝑥 (𝑠𝑒𝑐𝑥) = 𝑠𝑒𝑐𝑥𝑡𝑎𝑛𝑥 f. 𝐷𝑥 (𝑐𝑠𝑐𝑥) = −𝑐𝑠𝑐𝑥𝑐𝑜𝑡𝑥

The proof of (𝑎) will be presented below. Statement (𝑏) can be proven similarly.

Proof. Expanding 𝑠𝑖𝑛 (𝑥 + ℎ) using the trigonometric sum identity, we obtain

sin(𝑥 + ℎ) sin 𝑥
𝐷𝑥 (sin 𝑥) = lim
ℎ→0 ℎ

(sin 𝑥 cos ℎ + cos 𝑥 sin ℎ) sin 𝑥

= lim
ℎ→0 ℎ

Basic Calculus Page 12 of

17
Derivatives as the Slope of Tangent Line Week 7

sin ℎ 1 − cos ℎ
= lim cos 𝑥 ∙ + (− sin 𝑥) ∙
ℎ→0 ℎ ℎ

sin ℎ 1 − cos ℎ
= lim + (− sin 𝑥) ∙ lim
ℎ→0 ℎ ℎ→0 ℎ

= (cos 𝑥) (1)(sin 𝑥)(0)

= cos 𝑥

Statements (𝑐) − (𝑓) can be proved using Statements (𝑎) and (𝑏) and the Quotient Rule. We only present
the proof of (𝑐) below.

Proof. Using Quotient Rule and Statements (𝑎) and (𝑏) above, we have

sin 𝑥 cos 𝑥 𝐷𝑥 (sin 𝑥) − sin 𝑥 𝐷𝑥 (cos 𝑥)

𝐷𝑥 (tan 𝑥) = 𝐷𝑥 [ ]=
cos 𝑥 (cos 𝑥)2

cos 𝑥 (cos 𝑥) − (𝑠𝑖𝑛 𝑥)(− sin 𝑥)

=
(𝑐𝑜𝑠 2 )𝑥

𝑐𝑜𝑠 2 𝑥 + 𝑠𝑖𝑛2 𝑥
=
𝑐𝑜𝑠 2 𝑥

1
Using the identity 𝑐𝑜𝑠 2 𝑥 + 𝑠𝑖𝑛2 𝑥 = 1, we get 𝐷𝑥 (tan 𝑥) = 𝑐𝑜𝑠2𝑥 = 𝑠𝑒𝑐 2 𝑥

Example 1: Differentiate the following functions:

Basic Calculus Page 13 of

17
Derivatives as the Slope of Tangent Line Week 7

a.𝑓(𝑥) = 𝑠𝑒𝑐𝑥 + 3𝑐𝑠𝑐 𝑥 b.𝑔(𝑥) = 𝑥 2 𝑠𝑖𝑛𝑥 − 3𝑥𝑐𝑜𝑠𝑥 + 5𝑠𝑖𝑛𝑥

𝑓’(𝑥) = 𝑠𝑒𝑐 𝑥𝑡𝑎𝑛𝑥 + 3(−𝑐𝑠𝑐 𝑥𝑐𝑜𝑡𝑥) 𝑔’(𝑥) = [(𝑥 2 )(𝑐𝑜𝑠𝑥) + (𝑠𝑖𝑛𝑥)(2𝑥)] − 3[(𝑥)(−𝑠𝑖𝑛𝑥) + (𝑐𝑜𝑠𝑥(1)]
+ 5(𝑐𝑜𝑠)𝑥)]
= 𝑠𝑒𝑐𝑥𝑡𝑎𝑛𝑥 − 3 𝑐𝑠𝑐𝑥𝑐𝑜𝑡𝑥
= 𝑥 2 𝑐𝑜𝑠𝑥 + 2𝑥𝑠𝑖𝑛𝑥 + 3𝑥𝑠𝑖𝑛𝑥3 𝑐𝑜𝑠𝑥 + 5 𝑐𝑜𝑠𝑥

= 𝑥 2 𝑐𝑜𝑠𝑥 + 5𝑥𝑠𝑖𝑛𝑥 + 2 𝑐𝑜𝑠𝑥

✓ Whenever Rule 7 is applied to problems where the trigonometric functions are viewed as functions of
angles, the unit measure must be in radians.
✓ Every trigonometric function is differentiable on its domain. In particular, the sine and cosine functions
are everywhere differentiable.
Rule 8. Derivative of an exponential function

𝑖𝑓𝑓(𝑥) = 𝑒 𝑥 , 𝑡ℎ𝑒𝑛𝑓 ′ (𝑥) = 𝑒𝑥

Proof. (Optional) Using the definition of the derivative,

′ 𝑓(𝑥 + ℎ) − 𝑓(𝑥) 𝑒 𝑥+ℎ − 𝑒 𝑥

𝑓 (𝑥) = lim = lim
ℎ→0 ℎ ℎ→0 ℎ

𝑒 ℎ −1
Using a law of exponent, 𝑒 𝑥+ℎ − 𝑒 𝑥 ∙ 𝑒 ℎ . Therefore, since lim =1
ℎ→0 ℎ

′ (𝑥)
𝑒 𝑥 (𝑒 ℎ − 1) 𝑥
𝑒ℎ − 1
𝑓 = lim = 𝑒 ∙ lim = 𝑒𝑥
ℎ→0 ℎ ℎ→0 ℎ

a. Find𝑓’(𝑥)𝑖𝑓𝑓(𝑥) = 3𝑒 𝑥 b. Find 𝑔’(𝑥)𝑖𝑓𝑔(𝑥) = −4𝑥 2 𝑒 𝑥 + 5𝑥𝑒 𝑥 − 10𝑒 𝑥

Solution. Applying Rules 3 and 7, we have Solution. Applying Rule 5to the first two terms and
Rule 3 to the third term, we have
𝑓 ′ (𝑥) = 3𝐷𝑥 [𝑒 𝑥 ]

Basic Calculus Page 14 of

17
Derivatives as the Slope of Tangent Line Week 7

= 3𝑒 𝑥 𝑔′(𝑥) = [(−4𝑥 2 )(𝑒 𝑥 ) + (𝑒 𝑥 )(−8𝑥)] + [(5𝑥)(𝑒 𝑥 )(5)

− 10 ∙ 𝑒 𝑥 ]

= −4𝑥 2 𝑒 𝑥 − 3𝑥𝑒 𝑥 − 5𝑒 𝑥

c. Find ℎ’(𝑥)if 𝑑𝑦 17
d.Find 𝑑𝑥 where𝑦 = 𝑒 𝑥 𝑥 𝑒 +2𝑥−3
√𝑥

ℎ(𝑥) = 𝑒 𝑥 𝑠𝑖𝑛𝑥 − 3𝑒 𝑥 𝑐𝑜𝑠𝑥 3

𝑒 𝑥 𝑥 𝑒 + 2𝑥 − 3√𝑥(0) − (17)([(𝑒 𝑥 )(𝑒𝑥 𝑒−1 ) + (𝑥 𝑒 )(𝑒 𝑥 )] + 2 −
2√𝑥
=
(𝑒 𝑥 𝑥 𝑒 + 2𝑥 − 3√𝑥)2
Solution. We apply the Product Rule to each term.
51
−17𝑒 𝑥+1 𝑥 𝑒−1 − 17𝑒 𝑥 𝑥 𝑒 − 34 + 2
ℎ ′ (𝑥)
= [(𝑒 𝑥 )(cos 𝑥) + (sin 𝑥)(𝑒 𝑥 )]
−3 √𝑥
= 2
(𝑒 𝑥 𝑥 𝑒 + 2𝑥 − 3√𝑥)
∙ [(𝑒 𝑥 )(− sin 𝑥) + cos 𝑥)( 𝑒 𝑥 )]

= 𝑒 𝑥 cos 𝑥 + sin 𝑥 + 3𝑒 𝑥 sin 𝑥 − 3𝑒 𝑥 cos 𝑥

= 𝑒 𝑥 (4 sin 𝑥 − 2 cos 𝑥)

Conclusion/ Summary

✓ A tangent line to the function 𝑓(𝑥) at the point 𝑥 = 𝑎 is a line that just touches the graph of the
function at the point in question and is “parallel” (in some way) to the graph at that point.
✓ steps you use to find the equation of a tangent line to a curve at an indicated point:
1. Find the first derivative of 𝑓(𝑥).
2. Plug x value of the indicated point into 𝑓 ′(𝑥) to find the slope at 𝑥
3. Plug 𝑥 value into 𝑓(𝑥) to find the y coordinate of the tangent point.
4. Combine the slope from step 2 and point from step 3 using the point-slope formula to find the
equation for the tangent line.
5. Graph your results to see if they are reasonable.

Basic Calculus Page 15 of

17
Derivatives as the Slope of Tangent Line Week 7

✓ Rule 3 states that the derivative of constant times a differentiable function is the constant times the
derivative of the function. Its proof is a direct consequence of the constant multiple theorems for
limits.
✓ Rule 4 states that the derivative of the sum of two differentiable functions is the sum of the derivatives
of the functions. Its proof relies on the Addition Theorem for limits.
✓ Rule 5 states that the derivative of the product of two differentiable functions is the first function
times the derivative of the second function plus the second function times the derivative of the first
function.
✓ Every trigonometric function is differentiable on its domain. In particular, the sine and cosine functions
are everywhere differentiable.
𝑑
✓ The domain of the exponential function is the set of real numbers, and [𝑒 𝑥 ] = 𝑒 𝑥 , it follows that
𝑑𝑥

the exponential function is differentiable everywhere.

Reference Link

✓ https://gato-docs.its.txstate.edu/slac/Subject/Math/Calculus/Findting-the-Equation-of-a-Tangent-
Line/Finding
✓ https://www.khanacademy.org/math/ap-calculus-ab/ab-differentiation-1-new/ab-2-2/a/finding-
tangent-line-equations
✓ H. Anton, I. Bivens, S. Davis, Calculus: Early Transcendental, John Wiley and Sons, 7th Edition, 2002.
✓ L. Leithold, College Algebra and Trigonometry, Addison Wesley Longman Inc., 1989, reprinted-Pearson
Education Asia Pte. Ltd, 2002
✓ J. Stewart, The Calculus: Early Transcendentals, Brooks/Cole, 6th Edition, 2008.
✓ H. Anton, I. Bivens, S. Davis, Calculus: Early Transcendentals, John Wiley and Sons, 7th Edition, 2002.

Basic Calculus Page 16 of

17