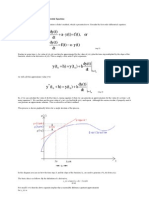
WRITE ABOUT THE EULER'S RULE WITH EXAMPLE

Euler's rule, also known as Euler's formula, is a fundamental equation in mathematics that
connects complex exponential functions, trigonometric functions, and the imaginary unit 'i'. It
is named after the Swiss mathematician Leonhard Euler and can be expressed as:
e^(iθ) = cos(θ) + i * sin(θ)
Here's a breakdown of Euler's rule and an example to illustrate its significance:
1. e^(iθ): This is a complex exponential function, where 'e' is the base of the natural
logarithm, 'i' is the imaginary unit (i² = -1), and 'θ' is a real number that represents an
angle in radians.
2. cos(θ): This term represents the cosine of the angle 'θ'.
3. sin(θ): This term represents the sine of the angle 'θ'.
Euler's rule states that the complex exponential function e^(iθ) can be expressed as a
combination of the trigonometric functions cosine and sine of the same angle 'θ'. In other
words, it establishes a profound connection between complex numbers and the trigonometric
functions. This relationship is particularly useful in various branches of mathematics, physics,
engineering, and signal processing.
Example:
Let's illustrate Euler's rule with a specific example:
Suppose we want to find e^(iπ/3), which is e raised to the power of (iπ/3). Using Euler's rule:
e^(iπ/3) = cos(π/3) + i * sin(π/3)
1. cos(π/3): The cosine of π/3 (or 60 degrees) is 1/2.
2. sin(π/3): The sine of π/3 (or 60 degrees) is √3/2.
So, we can calculate:
e^(iπ/3) = (1/2) + i * (√3/2)
This is a complex number in the polar form. In rectangular form, it becomes:
e^(iπ/3) = 1/2 + (i√3)/2
This complex number represents a point on the unit circle in the complex plane, with an angle
of π/3 (or 60 degrees) counterclockwise from the positive real axis. It's often referred to as the
complex number representing the cube root of unity.
Euler's rule is not only a fascinating mathematical relationship but also an invaluable tool in
solving problems that involve complex numbers, waves, and oscillations. It forms the basis
for many concepts in physics and engineering, especially in areas like quantum mechanics,
electrical engineering, and signal processing.