Unit 4: Hyperbolas

Lesson 4.2
Graphs and Properties of Hyperbolas
Contents
Introduction 1

Learning Objectives 2

Warm Up 2

Learn about It! 3

Parts, Equations, and Properties of Hyperbolas 3
Graphing Hyperbolas 6

Key Points 21

Key Formulas 22

Check Your Understanding 23

Challenge Yourself 25

Photo Credit 27

Bibliography 27

Key to Try It! 28

Unit 4: Hyperbolas
Lesson 4.2

Graphs and Properties of

Hyperbolas

Introduction
Cooling towers are heat-transferred devices used to remove waste heat by cooling down the
hot fluid. It is also used to cool hot water by transferring heat to the air that allows it to be
reused. Cooling towers are used in nuclear power plants or manufacturing industries. Why
do most of the cooling towers are hyperboloid in shape? This type of structure is more
resistant to external natural forces than straight buildings. Also, the wide base of the towers
provides strength to support the tall structure while a wide top opening enhances the
diffusion process of cooling efficiently.

4.2. Graphs and Properties of Hyperbolas 1

Unit 4: Hyperbolas
In this lesson, we will recall the parts and properties of hyperbolas and use them to draw
their graphs.

Learning Objectives
DepEd Competencies
In this lesson, you should be able to do the
following: • Graph a hyperbola in a rectangular

● Identify the different parts and properties coordinate system.

(STEM_PC11AG-Id-3)
of a hyperbola.
• Recognize the equation and
● Sketch the graph of a hyperbola.
important characteristics of a
hyperbola (STEM_PC11AG-Ie-1)

Warm Up
Equation of the Hyperbola 10 minutes
In this activity, you will be able to recall how to transform the equation of a hyperbola from
standard form to general form and vice versa.

Materials
● pen
● paper

Procedure
1. Transform the following equations into their respective forms.
𝑥2 𝑦2
a. Transform − = 1 in general form.
4 8

b. Transform 4𝑦 2 − 9𝑥 2 + 56𝑦 + 36𝑥 + 124 = 0 in standard form.

2. Answer the guide questions below.

4.2. Graphs and Properties of Hyperbolas 2

Unit 4: Hyperbolas
Guide Questions
1. How do you transform the equation of a hyperbola from standard to general form?
2. How do you transform the equation of a hyperbola from general to standard form?
3. How will you know if a given equation is a hyperbola?

Learn about It!

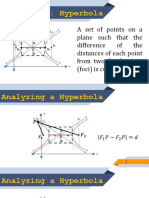
Recall that a hyperbola is defined as the set of all points on a plane whose absolute difference
between the distances from two fixed points 𝐹1 and 𝐹2 is constant. In this lesson, we will give
a summary of the parts and equations of the hyperbola. We will also analyze its properties
that will be used in graphing.

What are the important properties in graphing a

hyperbola?

Parts, Equations, and Properties of Hyperbolas

Fig. 4.2.1. below shows the parts of the hyperbola that you have learned in the previous
lesson.

Fig. 4.2.1. Parts of a hyperbola

4.2. Graphs and Properties of Hyperbolas 3

Unit 4: Hyperbolas
The two lines that the hyperbola approaches are called asymptotes. The ends of the
hyperbola approach the asymptotes.

The hyperbola also has a transverse axis and a conjugate axis, as shown in Fig. 4.2.2. with
the distances 𝑎, 𝑏, and 𝑐.

Fig. 4.2.2. Hyperbola with transverse and conjugate axis

The table below gives a summary of the different parts of a hyperbola.

Table 4.2.1. Parts of a hyperbola and its definition

Parts of a
Definition
Hyperbola

Principal axis a line passing through the foci of a hyperbola

Vertices two points on the hyperbola that lie on the principal axis

Center the midpoint of the transverse axis of the hyperbola

Foci two fixed points used to form the hyperbola

4.2. Graphs and Properties of Hyperbolas 4

Unit 4: Hyperbolas
Transverse axis a line segment joining the vertices; has length 2𝑎

a line segment passing through the center and is perpendicular to the

Conjugate axis
transverse axis with length 2𝑏

Asymptotes two lines that the hyperbola approaches

The hyperbola has two equations in standard form with center at (ℎ, 𝑘) depending on the
orientation of the principal axis.

Table 4.2.2. Equations of a hyperbola in standard form

Orientation of
Equation
Principal Axis

(𝒙 − 𝒉)𝟐 (𝒚 − 𝒌)𝟐
Horizontal − =𝟏
𝒂𝟐 𝒃𝟐

(𝒚 − 𝒌)𝟐 (𝒙 − 𝒉)𝟐
Vertical − =𝟏
𝒂𝟐 𝒃𝟐

Notice that 𝑎 2 is always in the denominator of the positive term. But, 𝑎 2 is not necessarily
greater than 𝑏2 .

The general form of the equation of the hyperbola is given by

𝑨𝒙𝟐 + 𝑩𝒚𝟐 + 𝑪𝒙 + 𝑫𝒚 + 𝑬 = 𝟎,

where 𝐴 and 𝐵 are not equal to 0 and have different signs. Thus, 𝐴𝐵 < 0. We transform the
general form of the equation of the hyperbola to standard form by completing the square.

4.2. Graphs and Properties of Hyperbolas 5

Unit 4: Hyperbolas

Remember
Since 𝐴 and 𝐵 have different signs, you might think that the general
equation of the hyperbola always follows the form
𝑨𝒙𝟐 − 𝑩𝒚𝟐 + 𝐶𝑥 + 𝐷𝑦 + 𝐸 = 0. This is not true since the equation of a
hyperbola can follow the form −𝑨𝒙𝟐 + 𝑩𝒚𝟐 + 𝐶𝑥 + 𝐷𝑦 + 𝐸 = 0.

The rule that we have to remember here is that 𝐴 and 𝐵 have different
signs.

What are the different parts of a hyperbola?

Graphing Hyperbolas
In graphing hyperbolas, we will follow the steps below:
1. Identify the center and orientation of the principal axis.
2. Find the distances 𝑎, 𝑏, and 𝑐.
3. Identify and plot the coordinates of the center, vertices, and foci. Plot as well the
endpoints of conjugate axis.
4. Sketch the asymptotes.
5. Sketch the hyperbola.

In graphing hyperbolas, we need to find the three distances 𝑎, 𝑏, and 𝑐, and draw the
asymptotes. The definitions of the three distances are given as follows.

4.2. Graphs and Properties of Hyperbolas 6

Unit 4: Hyperbolas
Table 4.2.3. Distances formed in a hyperbola

Distances Definition

distance from the center to a vertex; half the

𝒂
length of the transverse axis

𝒃 half the length of the conjugate axis

focal distance; distance from the center to a

𝒄
focus

Recall that the relationship between the three distances is 𝒂𝟐 + 𝒃𝟐 = 𝒄𝟐 . Thus, 𝑐 is always
greater than 𝑎 or 𝑏.

Notice that the two asymptotes of the hyperbola pass through the corners of a rectangle. This
rectangle is the auxiliary rectangle. Its center is the center of the hyperbola, and its width
and height are the length of the transverse and conjugate axes, respectively. By plotting the
vertices and using these asymptotes, we can sketch the graph of the hyperbola as shown in
Fig. 4.2.3.

Fig. 4.2.3. The auxiliary rectangle in a graph of a hyperbola

4.2. Graphs and Properties of Hyperbolas 7

Unit 4: Hyperbolas

Did You Know?

We can generate an equation for the asymptotes of the hyperbola.

When the principal axis of a hyperbola is horizontal, the equations of

its asymptotes are given by

𝑏
𝑦 − 𝑘 = ± 𝑎 (𝑥 − ℎ).

When the principal axis of a hyperbola is vertical, the equations of its

asymptotes are given by

𝑎
𝑦 − 𝑘 = ± 𝑏 (𝑥 − ℎ).

Let’s Practice!

Example 1
Determine the center of the hyperbola and the orientation of its principal axis represented
by the equation below.

(𝑥 − 2)2 (𝑦 − 3)2
− =1
4 9

Solution
Step 1: Determine the principal axis of the hyperbola.

(𝑥−ℎ)2 (𝑦−𝑘)2
This equation follows the form 𝑎2
− 𝑏2
= 1. This is the standard form of a

hyperbola with a horizontal principal axis. Thus, the orientation of its principal
axis is horizontal.

4.2. Graphs and Properties of Hyperbolas 8

Unit 4: Hyperbolas
Step 2: Determine the center of the hyperbola.

Note that the center of the hyperbola is located at (ℎ, 𝑘). In the given equation,
ℎ = 2 and 𝑘 = 3. Thus, the center is at (𝟐, 𝟑).

1 Try It!
Determine the center of the hyperbola and the orientation of its principal axis
represented by the equation below.

𝑥 2 (𝑦 + 1)2
− =1
16 4

Example 2
Find the distances 𝑎, 𝑏, and 𝑐 of the hyperbola represented by the equation below.

(𝑥 − 2)2 (𝑦 − 3)2
− =1
4 9

Solution
Step 1: Solve for 𝑎 and 𝑏.

(𝑥−ℎ)2 (𝑦−𝑘)2
The hyperbola is of the form − = 1 where 𝑎 2 = 4, and 𝑏2 = 9.
𝑎2 𝑏2

It follows that 𝒂 = 𝟐 and 𝒃 = 𝟑. Note that 𝑎 and 𝑏 are always positive, so we use
the principal square root.

Step 2: Solve for 𝑐.

To determine the value of 𝑐, we will use the equation 𝑎 2 + 𝑏2 = 𝑐 2 .

4.2. Graphs and Properties of Hyperbolas 9

Unit 4: Hyperbolas
𝑐2 = 𝑎2 + 𝑏2
𝑐 = √𝑎 2 + 𝑏 2
𝑐 = √4 + 9
𝑐 = √13

Therefore, 𝒂 = 𝟐, 𝒃 = 𝟑, and 𝒄 = √𝟏𝟑.

2 Try It!
Find the distances 𝑎, 𝑏, and 𝑐 of the hyperbola represented by the equation below.

𝑥 2 (𝑦 + 1)2
− =1
16 4

Example 3
Determine the coordinates of the endpoints of the transverse and conjugate axes of the
hyperbola represented by the equation below.

𝑦 2 𝑥2
− =1
4 25

Solution
Step 1: Identify the center and orientation of the principal axis.

(𝑦−𝑘)2 (𝑥−ℎ)2
Note that the equation follows the form − = 1. This is the standard
𝑎2 𝑏2

form of a hyperbola with center (ℎ, 𝑘) and with a vertical principal axis. Thus,
the principal axis of the hyperbola is vertical, and its center is at (𝟎, 𝟎).

4.2. Graphs and Properties of Hyperbolas 10

Unit 4: Hyperbolas
Step 2: Find the distances 𝑎 and 𝑏.

In the given equation, it can be observed that 𝑎 2 = 4 and 𝑏2 = 25. Thus, 𝒂 = 𝟐

and 𝒃 = 𝟓. Note that 𝑎 and 𝑏 are always positive, so we use the principal square
root.

Step 3: Find the endpoints of the transverse and conjugate axes.

Since the center of the hyperbola is at (0, 0) and it has a vertical principal axis,
the endpoints of its transverse axis are 𝑎 = 2 units above and below its center.
Therefore, the endpoints of the transverse axis are (𝟎, 𝟐) and (𝟎, −𝟐). These are
the vertices of the hyperbola.

Moreover, the endpoints of its conjugate axis are 𝑏 = 5 units to the left and the
right of its center. Therefore, the endpoints of the conjugate axis are (−𝟓, 𝟎)
and (𝟓, 𝟎).

3 Try It!
Determine the coordinates of the endpoints of the transverse and conjugate axes of
the hyperbola represented by the equation below.

𝑦 2 𝑥2
− =1
9 16

4.2. Graphs and Properties of Hyperbolas 11

Unit 4: Hyperbolas
Example 4
Determine the coordinates of the endpoints of the transverse and conjugate axes of the
hyperbola represented by the equation below.

(𝑥 + 1)2 (𝑦 − 1)2
− =1
25 9

Solution
Step 1: Identify the center and orientation of the principal axis.

(𝑥−ℎ)2 (𝑦−𝑘)2
The given equation follows the form − = 1, which is the standard
𝑎2 𝑏2

form of a hyperbola with center (ℎ, 𝑘) and with a horizontal principal axis. Thus,
the principal axis of the hyperbola is horizontal, and its center is at (−𝟏, 𝟏).

Step 2: Find the length of 𝑎 and 𝑏.

In the given equation, it follows that 𝑎 2 = 25 and 𝑏 2 = 9. Thus, 𝒂 = 𝟓 and 𝒃 = 𝟑.

Step 3: Find the endpoints of the transverse and conjugate axes.

Since the center of the hyperbola is at (−1, 1) and it has a horizontal principal
axis, the endpoints of its transverse axis are 𝑎 = 5 units to the left and the right
of its center. Therefore, the endpoints of the transverse axis are (−𝟔, 𝟏) and
(𝟒, 𝟏). These are the vertices of the hyperbola.

Moreover, the endpoints of its conjugate axis are 𝑏 = 3 units above and below
its center. Therefore, the endpoints of the conjugate axis are (−𝟏, −𝟐) and
(−𝟏, 𝟒).

4.2. Graphs and Properties of Hyperbolas 12

Unit 4: Hyperbolas
The graphs of the axes are shown below.

4 Try It!
Determine the coordinates of the endpoints of the transverse and conjugate axes of
the hyperbola represented by the equation below.

(𝑦 − 2)2 (𝑥 + 1)2
− =1
25 9

Example 5
Sketch the graph of the hyperbola represented by the equation below.

𝑥2 𝑦 2
− =1
4 9

Solution
Step 1: Identify the center and the orientation of the principal axis.

(𝑥−ℎ)2 (𝑦−𝑘)2
The equation follows the form − = 1, which is the standard form of
𝑎2 𝑏2

a hyperbola with center (ℎ, 𝑘) and with a horizontal principal axis. Thus, the
principal axis of the hyperbola is horizontal, and its center is at (𝟎, 𝟎).

4.2. Graphs and Properties of Hyperbolas 13

Unit 4: Hyperbolas
Step 2: Find the distances 𝑎, 𝑏, and 𝑐.

In the given equation, it follows that 𝑎 2 = 4 and 𝑏 2 = 9. Thus, 𝑎 = 2 and 𝑏 = 3.

To determine the value of 𝑐, we will use the equation 𝑎 2 + 𝑏2 = 𝑐 2 .

𝑐2 = 𝑎2 + 𝑏2
𝑐 = √𝑎 2 + 𝑏 2
𝑐 = √4 + 9
𝑐 = √13

Therefore, 𝒂 = 𝟐, 𝒃 = 𝟑, and 𝒄 = √𝟏𝟑.

Step 3: Identify and plot the coordinates of the center, vertices, and foci.

Since the center of the hyperbola is at (0, 0) and it has a horizontal principal
axis, the endpoints of its transverse axis are 𝑎 = 2 units to the left and to the
right of its center. Therefore, the endpoints of the transverse axis are (−𝟐, 𝟎)
and (𝟐, 𝟎). These are the vertices of the hyperbola.

The endpoints of its conjugate axis are 𝑏 = 3 units above and below its center.
Therefore, the endpoints of the conjugate axis are (𝟎, 𝟑) and (𝟎, −𝟑).

The hyperbola’s foci are 𝑐 = √13 units to the left and the right of its center.
Therefore, the coordinates of the foci are (−√𝟏𝟑, 𝟎) and √𝟏𝟑, 𝟎).

4.2. Graphs and Properties of Hyperbolas 14

Unit 4: Hyperbolas

Step 4: Sketch the asymptotes.

Draw the auxiliary rectangle of the hyperbola. Then, draw two asymptotes
that pass through the corners of the rectangle.

4.2. Graphs and Properties of Hyperbolas 15

Unit 4: Hyperbolas
Step 5: Sketch the hyperbola.

The hyperbola passes through the vertices and approaches the asymptotes.
The blue curve below is the graph of the hyperbola.

5 Try It!
Sketch the graph of the hyperbola represented by the equation below.

𝑦 2 𝑥2
− =1
4 9

4.2. Graphs and Properties of Hyperbolas 16

Unit 4: Hyperbolas
Example 6
Sketch the graph of the hyperbola represented by the equation below.

(𝑦 + 3)2
− (𝑥 − 4)2 = 1
16

Solution
Step 1: Identify the center and orientation of the principal axis.

(𝑦−𝑘)2 (𝑥−ℎ)2
The equation follows the form − = 1, which is the standard form of
𝑎2 𝑏2

a hyperbola with center (ℎ, 𝑘) and with a vertical principal axis. Thus, the
principal axis of the hyperbola is vertical, and its center is at (𝟒, −𝟑).

Step 2: Find the distances 𝑎, 𝑏 and 𝑐.

In the given equation, it follows that 𝑎 2 = 16 and 𝑏2 = 1. Thus, 𝒂 = 𝟒 and 𝒃 = 𝟏.

To determine the value of 𝑐, we will use the equation 𝑎 2 + 𝑏2 = 𝑐 2 .

𝑐2 = 𝑎2 + 𝑏2
𝑐 = √𝑎 2 + 𝑏 2
𝑐 = √16 + 1
𝑐 = √17

Therefore, 𝒂 = 𝟒, 𝒃 = 𝟏, and 𝒄 = √𝟏𝟕.

Step 3: Identify and plot the coordinates of the center, vertices, and foci.

Since the center of the hyperbola is at (4, −3), and it has a vertical principal axis,
the endpoints of its transverse axis are 𝑎 = 4 above and below its center.

4.2. Graphs and Properties of Hyperbolas 17

Unit 4: Hyperbolas
The endpoints of the transverse axis are (𝟒, 𝟏) and (𝟒, −𝟕). These are the
vertices of the hyperbola.

The endpoints of its conjugate axis are 𝑏 = 1 unit to the left and to the right of
its center. Therefore, the endpoints of the conjugate axis are (𝟑, −𝟑) and
(𝟓, −𝟑).

The hyperbola’s foci are 𝑐 = √17 units above and below its center. Therefore,
the coordinates of the foci are (𝟒, −𝟑 + √𝟏𝟕) and (𝟒, −𝟑 − √𝟏𝟕).

4.2. Graphs and Properties of Hyperbolas 18

Unit 4: Hyperbolas
Step 4: Sketch the asymptotes.

Draw the auxiliary rectangle of the hyperbola. Then, draw two asymptotes
that pass through the corners of the rectangle.

4.2. Graphs and Properties of Hyperbolas 19

Unit 4: Hyperbolas
Step 5: Sketch the hyperbola.

The hyperbola passes through the vertices and approaches the asymptotes.
The blue curve below is the graph of the hyperbola.

6 Try It!
Sketch the graph of the hyperbola below.

(𝑥 − 4)2
− (𝑦 + 3)2 = 1
16

4.2. Graphs and Properties of Hyperbolas 20

Unit 4: Hyperbolas
Key Points
___________________________________________________________________________________________

● A hyperbola is defined as the set of all points on a plane whose absolute difference
between the distances from two fixed points 𝐹1 and 𝐹2 is constant.

● The parts of the hyperbola are the principal axis, vertices, center, foci, transverse
axis, conjugate axis, and asymptotes.

● The standard form of the equation of a hyperbola with center at (ℎ, 𝑘) and with a
(𝒙−𝒉)𝟐 (𝒚−𝒌)𝟐
horizontal principal axis is given by − = 𝟏, while the standard form of
𝒂𝟐 𝒃𝟐

the equation of a hyperbola with center at (ℎ, 𝑘) and with a vertical principal axis is
(𝒚−𝒌)𝟐 (𝒙−𝒉)𝟐
given by − = 𝟏.
𝒂𝟐 𝒃𝟐

● The length 𝒂 is the distance from the center to a vertex and is half the length of the
transverse axis. The length 𝒃 is half the length of the conjugate axis. The length 𝒄,
called the focal distance, is the distance from the center to a focus.

● The relationship between the three distances is 𝒂𝟐 + 𝒃𝟐 = 𝒄𝟐 .

● In graphing hyperbolas, follow the steps below:

1. Identify the center and orientation of the principal axis.
2. Find the distances 𝑎, 𝑏, and 𝑐.
3. Identify and plot the coordinates of the center, vertices, and foci. Plot as well
the endpoints of conjugate axis.
4. Sketch the asymptotes.
5. Sketch the hyperbola.
___________________________________________________________________________________________

4.2. Graphs and Properties of Hyperbolas 21

Unit 4: Hyperbolas
Key Formulas
___________________________________________________________________________________________

Concept Formula Description

Relationship 𝑎2 + 𝑏2 = 𝑐 2 , Use this formula to find an

between the values unknown distance (e.g.,
𝒂, 𝒃, and 𝒄 where 𝑎 is the distance from the focal distance) when the
center to a vertex, 𝑏 is the other values are known.
distance from the center to an
endpoint of the conjugate axis,
and 𝑐 is the focal distance.

Use this formula to find the

Equation of a (𝑥 − ℎ)2 (𝑦 − 𝑘)2
− = 1, equation of a hyperbola
Hyperbola in 𝑎2 𝑏2
given its center, 𝑎, and 𝑏 if
Standard Form where the transverse axis is
• (ℎ, 𝑘) is the center; horizontal.
• 𝑎 is the distance from the
center to a vertex, and
• 𝑏 is the distance from the
center to an endpoint of
the conjugate axis.

Use this formula to find the

(𝑦 − 𝑘)2 (𝑥 − ℎ)2
− = 1, equation of a hyperbola
𝑎2 𝑏2
given its center, 𝑎, and 𝑏 if
where the transverse axis is
• (ℎ, 𝑘) is the center; vertical.
• 𝑎 is the distance from the
center to a vertex, and
• 𝑏 is the distance from the
center to an endpoint of
the conjugate axis.

4.2. Graphs and Properties of Hyperbolas 22

Unit 4: Hyperbolas

Equation of a 𝐴𝑥 2 + 𝐵𝑦 2 + 𝐶𝑥 + 𝐷𝑦 + 𝐸 = 0 This is the equation of a

Hyperbola in hyperbola when the
General Form where 𝐴 and 𝐵 are not equal to 0, standard form is expanded.
and they have different signs.

___________________________________________________________________________________________

Check Your Understanding

A. For each item, identify the part of the hyperbola that is being
described by the statement.

1. It is a line passing through the foci of the hyperbola.

2. These are two points that lie on the hyperbola along the principal axis.
3. It is a line segment joining the vertices of the hyperbola.
4. It is a line segment with length 2𝑏 and whose midpoint is the center of the hyperbola.
5. These are two lines that the hyperbola approaches.

B. Determine the center and orientation of the principal axis

of the following hyperbolas.

𝑥2 𝑦2
1. − =1
4 5
𝑥2
2. 𝑦 2 − =1
4
(𝑦−2)2 (𝑥+1)2
3. − =1
9 4
(𝑥−2)2 (𝑦+6)2
4. − =1
8 8
(𝑥−3)2 𝑦2
5. =1+
36 9

4.2. Graphs and Properties of Hyperbolas 23

Unit 4: Hyperbolas
C. Find the length of 𝑎, 𝑏, and 𝑐 of the following hyperbolas.

1. 𝑦 2 − 𝑥 2 = 1
𝑥2 𝑦2
2. − =1
4 5
(𝑦−2)2 (𝑥+1)2
3. − =1
9 4
(𝑦−1)2 (𝑥−3)2
4. − =1
36 49
(𝑥+7)2 (𝑦+6)2
5. − =1
81 25

D. Graph the following hyperbolas.

𝑥2 𝑦2
1. − 25 = 1
9
𝑦2
2. − 𝑥2 = 1
4
(𝑥+1)2 (𝑦+2)2
3. − =1
36 16
(𝑦+4)2 (𝑥−3)2
4. − =1
9 16
(𝑦+1)2
5. (𝑥 + 5)2 − =1
9

4.2. Graphs and Properties of Hyperbolas 24

Unit 4: Hyperbolas

Challenge Yourself

Answer the following questions.

1. Graph the hyperbola 16𝑥 2 − 𝑦 2 + 32𝑥 = 0.

2. Graph the hyperbola 9𝑦 2 − 4𝑥 2 − 36𝑦 − 32𝑥 + 8 = 0.
3. What is the equation of the hyperbola given below in standard form?

4.2. Graphs and Properties of Hyperbolas 25

Unit 4: Hyperbolas
4. What is the equation of the hyperbola given below in standard form?

5. What is the equation of the hyperbola given below in general form?

4.2. Graphs and Properties of Hyperbolas 26

Unit 4: Hyperbolas

Photo Credit
Cooling towers of Dukovany Nuclear Power Plant in Dukovany, Třebíč District.jpg by Jiří
Sedláček is licensed under CC BY-SA 4.0 via Wikimedia Commons.

Bibliography
Barnett, Raymond, Michael Ziegler, Karl Byleen, and David Sobecki. College Algebra with
Trigonometry. Boston: McGraw Hill Higher Education, 2008.

Bittinger, Marvin L., Judith A. Beecher, David J. Ellenbogen, and Judith A. Penna. Algebra and
Trigonometry: Graphs and Models. 4th ed. Boston: Pearson/Addison Wesley, 2009.

Blitzer, Robert. Algebra and Trigonometry. 3rd ed. Upper Saddle River, New Jersey:
Pearson/Prentice Hal, 2007.

Larson, Ron. College Algebra with Applications for Business and the Life Sciences. Boston:
MA:Houghton Mifflin, 2009.

Safier, Fred. Schaum’s Outlines of Precalculus. New York, N.Y: McGraw-Hill, 2013.

Simmons, George F. Calculus with Analytic Geometry. 2nd ed. New York: McGraw-Hill, 1996.

4.2. Graphs and Properties of Hyperbolas 27

Unit 4: Hyperbolas

Key to Try It!

1. center at (0, −1); horizontal
2. 𝑎 = 4, 𝑏 = 2, 𝑐 = 2√5
3. endpoints of transverse axis: (0, 3), (0, −3); endpoints of conjugate axis: (4, 0), (−4, 0)
4. endpoints of transverse axis: (−1, −3), (−1, 7); endpoints of conjugate axis: (2, 2),
(−4, 2)
5.

6.

4.2. Graphs and Properties of Hyperbolas 28