Arguments and Polar Form of Complex Numbers

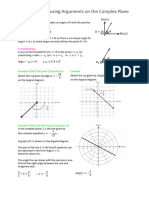
Argument of 𝑧
The argument of a complex number is the angle measured anticlockwise
from the positive real axis. The argument can be any of the coterminal
angles that align with complex number. That is, all complex numbers on the
same ray from the origin, except the origin, will have the same argument.

arg(0 + 0𝑖) is not defined, as there is no unique or periodic

angle that defines the point. That is, if |𝑧| = 0, then
𝑧 = 0 cis(𝜃) = 0 regardless of what 𝜃 is.

To determine the argument of a complex number, trigonometry can be used

to find an acute reference angle that can then be put in the correct quadrant
using the real and imaginary parts.
When the complex number is purely imaginary inverse tangent is undefined.
𝜋
The argument is either coterminal to ⎯⎯when it is a positive imaginary number
2
𝜋
or coterminal to − ⎯⎯when it is a negative imaginary number.
2
Example Example Example Example
⎯⎯ ⎯⎯ ⎯⎯ ⎯⎯
arg √3 + 𝑖 arg −√3 + 𝑖 arg −√3 − 𝑖 arg √3 − 𝑖
𝜋 13𝜋 11𝜋 5𝜋 17𝜋 7𝜋 7𝜋 19𝜋 5𝜋 11𝜋 23𝜋 𝜋
= ⎯⎯, ⎯⎯⎯⎯, − ⎯⎯⎯⎯, … = ⎯⎯⎯, ⎯⎯⎯⎯, − ⎯⎯⎯, … = ⎯⎯⎯, ⎯⎯⎯⎯, − ⎯⎯⎯, … = ⎯⎯⎯⎯, ⎯⎯⎯⎯, − ⎯⎯, …
6 6 6 6 6 6 6 6 6 6 6 6

Principal Argument
Since the argument of a complex number is not unique, we
introduce the principal argument as the unique argument within
one revolution from −𝜋 to 𝜋 for each complex number.

The principal argument of a complex number 𝑧 is denoted

Arg(𝑧), so −𝜋 < Arg(𝑧) ≤ 𝜋. We use a capital A for the
principal argument to distinguish it from all other arguments.

Example
Evaluate Arg(−1 − 𝑖).
1 𝜋 𝜋 3𝜋
−1 − 𝑖 is in Q3 and the reference angle is tan ⎯⎯ = ⎯⎯. ∴ Arg(−1 − 𝑖) = −𝜋 + ⎯⎯= − ⎯⎯⎯
1 4 4 4

Example VCAA 2005 Exam 1 Question 6

3 − 6𝑖
If 𝑧 = ⎯⎯⎯⎯⎯⎯, then |𝑧| and Arg(𝑧) are, respectively
2+𝑖

3 − 6𝑖 3 − 6𝑖 2 − 𝑖 6 − 12𝑖 − 3𝑖 + 6𝑖 (6 − 6) + (−12 − 3)𝑖 −15𝑖

⎯⎯⎯⎯⎯⎯= ⎯⎯⎯⎯⎯⎯× ⎯⎯⎯⎯ = ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯= ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ = ⎯⎯⎯⎯⎯= −3𝑖
2+𝑖 2+𝑖 2−𝑖 4−𝑖 4+1 5
𝜋
|𝑧| = |−3𝑖| = 3, Arg(−3𝑖) = − ⎯⎯(since − 3𝑖 is on the negative 𝑦-axis)
2

Example VCAA 2016 Exam 2 Question 5

2𝜋 2𝜋 ⎯⎯ 𝑎 ⎯⎯
If Arg(−1 + 𝑎𝑖) = − ⎯⎯⎯, then the real number 𝑎 is tan − ⎯⎯⎯ = √3 = ⎯⎯⎯ ⇒ 𝑎 = −√3
3 3 −1

Polar Form / Modulus and Argument Form

Polar Form / Modulus and Argument Form
Complex numbers need a pair of values to uniquely define them. Cartesian form uses the real and
imaginary parts as its coordinate. Polar form uses the magnitude and principal argument for its
coordinate. Trigonometry connects the two coordinate systems together.
Re(𝑧) = 𝑟 cos(𝜃) , Im(𝑧) = 𝑟 sin(𝜃), where 𝜃 = Arg(𝑧) and 𝑟 = |𝑧|
𝑧 = Re(𝑧) + 𝑖 Im(𝑧) = 𝑟 cos(𝜃) + 𝑖(𝑟 sin(𝜃)) = 𝑟(cos(𝜃) + 𝑖 sin(𝜃))
We contract cos(𝜃) + 𝑖 sin(𝜃) as cis(𝜃), so 𝑧 = 𝑟 cis(𝜃) .

Modulus in Polar Form

The distance from the origin to a point.
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
|𝑧| = (𝑟 cos(𝜃)) + (𝑟 sin(𝜃)) = 𝑟 (cos (𝜃) + sin (𝜃)) = |𝑟|

Converting from Cartesian Form to Polar Form

The polar form of 𝑧 is |𝑧| cis(Arg(𝑧)).
That is, we need to calculate the modulus, |𝑧|: |𝑧| = [Re(𝑧)] + [Im(𝑧)] and we need to calculate
the principal argument, Arg(𝑧), using trigonometry and the quadrant the complex number is in.

Example VCAA 2014 Exam 2 Question 2ai Example VCAA 2008 Exam 2 Question 8
⎯⎯ In polar form, the complex number 𝑖 − 1 is
Express √3 − 3𝑖 in polar form.
⎯⎯ ⎯⎯⎯⎯⎯ ⎯⎯⎯ ⎯⎯ ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ ⎯⎯
√3 − 3𝑖 = √3 + 9 = √12 = 2√3 |𝑖 − 1| = (−1) + 1 = √2
⎯⎯ 𝑖 − 1 is in Q2 and the reference angle is:
√3 − 3𝑖 is in Q4 and the reference angle is
3 ⎯⎯ 𝜋 1 𝜋
tan ⎯⎯⎯ tan ⎯⎯ = ⎯⎯
⎯⎯ = tan √3 = ⎯⎯ 3 1 4
√3
⎯⎯ 𝜋 𝜋 3𝜋
Arg √3 − 3𝑖 = − ⎯⎯ Arg(𝑖 − 1) = 𝜋 − ⎯⎯= ⎯⎯⎯
3 4 4
⎯⎯ ⎯⎯ 𝜋 ⎯⎯ 3𝜋
∴ √3 − 3𝑖 = 2√3 cis − ⎯⎯ ∴ 𝑖 − 1 = √2 cis ⎯⎯⎯
3 4
Converting from Polar Form to Cartesian Form
The Cartesian form of 𝑟 cis(𝜃) is 𝑟 cos(𝜃) + 𝑟 sin(𝜃) 𝑖.
That is, we expand cis(𝜃) to cos(𝜃) + 𝑖 sin(𝜃) and evaluate the real and imaginary parts.

Example
5𝜋
Express 8 cis ⎯⎯⎯ in Cartesian form.
6
⎯⎯
5𝜋 5𝜋 5𝜋 √3 1 ⎯⎯
8 cis ⎯⎯⎯ = 8 cos ⎯⎯⎯ + 𝑖 sin ⎯⎯⎯ = 8 − ⎯⎯⎯+ ⎯⎯𝑖 = −4√3 + 4𝑖
6 6 6 2 2

Example
⎯⎯ 𝜋
Express 2√3 cis − ⎯⎯ in Cartesian form.
3 ⎯⎯
⎯⎯ 𝜋 ⎯⎯ 𝜋 𝜋 ⎯⎯ 1 √3 ⎯⎯
2√3 cis − ⎯⎯ = 2√3 cos − ⎯⎯ + 𝑖 sin − ⎯⎯ = 2√3 ⎯⎯− ⎯⎯⎯𝑖 = √3 − 3𝑖
3 3 3 2 2

Complex Conjugate of 𝑧, 𝑧̅
The complex number with the opposite imaginary value.
That is, a reflection of a complex number in the real axis.
For a complex number in polar form: 𝑧̅ = 𝑟 cis(𝜃) = 𝑟 cis(−𝜃)

Example Example
2𝜋 2𝜋 6 cis(−1.34) = 6 cis(1.34)
2 cis ⎯⎯⎯ = 2 cis − ⎯⎯⎯
3 3
Example
6 cis(𝜋) = 6 cis(−𝜋) = 6 cis(𝜋)