Republic of the Philippine

ZAMBOANGA PENINSULA POLYTECHNIC STATE UNIVERSITY

COLLEGE OF ENGINEERING AND TECHNOLOGY
R.T. Lim Blvd., Baliwasan, Zamboanga City

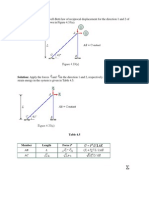
MODULE 4 - VECTORS AND SPACE 4.3.2. A force of 400kN is passing from A(1, 2, 7) to B(-2, 3, 5).
Find the components of the force.
ANALYTIC GEOMETRY
SITUATION:
(Part – 1)
A concurrent forc system in space is composed of 3 forces
4.1. INTRODUCTION TO VECTOR described as follows: A= 100kN acts through point (2, 6, 8) and
(1, 4, 2). B= 330kN and acts through the point (2, 6, 8) and (4,
4.1.1. Evaluate the magnitude of the vector F=4i + 7j-5k. 1, -2). C= 85kN and acts through the point (2, 6, 8) and (2, -3,
4.1.2. Define the vector whose head is at (-3, 0, -7) and tail at 3).
(1, -8, 12). 4.3.3. what is the x- component of the resultant force.
4.1.3. Three vectors A, B, and C are defined as follows: 4.3.4. what is the y-component of the resultant force.
A= 2i +4j – 6k 4.3.5. what is the z- component of the resultant force.
B= i + 8j -4k 4.3.6. what is the resultant force?
C= 5i +3k 4.4. APPLICATION OF VECTORS TO WORK AND MOMENT
Determine the resultant of vectors A, B, and C. and also the 4.4.1. a constant force of 200N acts from (3, -4, 5) to (6, 7, -1).
magnitude of this resultant. Find the work done of this force in moving object from point of
SITUATION: A(5, 6,-1) to B(6, 7, -4) in a straight line. The coordinates are in
meters.
Let A= (2 -3 6), B= (1 8 4)
4.4.2. a force of 200N acts from A(3, -2, 5) to B(4, 6, -3). What
is the moment of the 200N force about (9,7,-1).
4.1.4. Determine A + B 4.5. APPLICATION OF VECTORS IN GEOMETRY
4.1.5. Determine |A + B| 4.5.1. what is the perpendicular distance of line AB that passes
from A(3, 4, 5) to B(4, -4, 7) from point C(6, 1, -7)?
4.1.6. Determine A • B
4.5.2. what is the shortest distance of point (5, 8, 9) from x-
4.1.7. Determine A X B axis.
4.1.8. Determine |A X B|
4.5.3. What is the area of parallelogram formed by vectors 3i
4.1.9. Given two vectors: +2j and 3j – 4k.

A= <2 4 6> 4.5.4. Find the volume of parallelepiped formed by the vectors
1i +1j + 1k, 2i – j – 3k, 3j – k.
B= <1 8 -4>
4.5.5. Find the distance between the points A(4, 8,-1) and B(9,
What would be the angle between them? 1, 2)?
4.2. UNIT VECTOR AND DIRECTION COSINE

SITUATION:

Let A= (2 -3 6), B= (1 8 4)

4.2.1. Find the unit vector of A.

4.2.2. Find the unit vector of B.

4.2.3. Find the direction cosine of A.

4.2.4. Find the dircetion cosine of B.

4.2.5. Determine the angle that vector A= 2i + 4j - 6k makes

with the positive x, y, and z axis.

4.2.6. Find the unit vector parallel to the sum of the vector A=
<2 4 -5>, and B= <1 2 3>

4.3. APPLICATION OF VECTORS TO CONCURRENT FORCE

SYSTEM

4.3.1. F= 100kN force passes through point A (1, 4, 9) to B (8,

9, 12). Evaluate Fx, Fy, and Fz.