Professional Documents
Culture Documents
4
4
Uploaded by
jkhy781500 ratings0% found this document useful (0 votes)
6 views5 pagesvisual identification of soils is an important field and laboratory procedure for
developing an approximate grain size distribution curve (Fig. 3.1). This curve can be
used to evaluate the suitability of a
Copyright
© © All Rights Reserved
Available Formats
TXT, PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this Documentvisual identification of soils is an important field and laboratory procedure for
developing an approximate grain size distribution curve (Fig. 3.1). This curve can be
used to evaluate the suitability of a
Copyright:
© All Rights Reserved
Available Formats
Download as TXT, PDF, TXT or read online from Scribd
Download as txt, pdf, or txt
0 ratings0% found this document useful (0 votes)
6 views5 pages4
4
Uploaded by
jkhy78150visual identification of soils is an important field and laboratory procedure for
developing an approximate grain size distribution curve (Fig. 3.1). This curve can be
used to evaluate the suitability of a
Copyright:
© All Rights Reserved
Available Formats
Download as TXT, PDF, TXT or read online from Scribd
Download as txt, pdf, or txt
You are on page 1of 5
Meyerhof also found higher values of f3 for tapered
piles, reflecting the higher horizontal stresses produced.
For piles bored or driven into stiff overconsolidated
clays the Ko and hence Ks value can be expected to vary
with depth. Meyerhof (1976) stated that, for bored
piles, Ks varies from about 0.7 Ko to 1.2 Ko but for
driven piles it varies from about Ko to more than 2Ko'
Randolph and Wroth (1982) suggest a relationship
between f3 and the ratio c / (j '. However, although it u v
is clear that shaft resistance is governed by effective
stresses, the empirical correlations required to determine
values of f3 make this approach no better than the
traditional total stress or a method, at the present time.
Driven piles in sand
Effects of installation
Driving piles into loose sands compacts them, increasing
their density and angle of internal friction and
increasing the horizontal stresses around the pile.
Driving piles into dense sands may not compact
them. Instead, dilatancy and negative pore pressures
may temporarily increase the pile load capacity, make
driving difficult and possibly result in overstressing
and damage to the pile. Dissipation of this negative
pore pressure after driving will cause the pile load
capacity to decrease so a false impression of load
capacity can be derived from the driving records. This
is often referred to as relaxation.
The extent to which driving may increase the
density of the sand could be up to 4-6 diameters away
from the pile and 3-5 diameters below the pile (Broms,
1966). This zone of influence is larger for loose
sands than dense sands and will obviously affect the
driving of piles in groups where piles are typically
2-3 diameters apart.
It is also presumed that the sands are hard, clean
quartz grains which will not deteriorate under driving
stresses. Softer crushable grains will produce lower
angles of friction after driving and be more compressible.
The design of a pile must consider installation
effects and the final state of the sand. It can only be
considered as approximate and should be checked by
in situ pile loading tests.
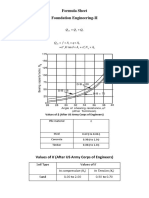
End bearing resistance qb (Figure 10.7)
The conventional approach to end bearing resistance is
to use the surcharge term of the bearing capacity
equation (Equation 8.11) as c' = 0 and the width of a
pile is small compared to its length:
(10.15)
where 0' is the vertical effective stress at the base of v
the pile and N is a bearing capacity factor. The values q
of N provided by Berezantsev et al (1961) are comq
monly used, Figure 10.7.
\000
/
/'
L
\00 /
./
./
/'
/'
/
V
30 35 40 45
Angle of internal friction 1/>'
Figure 10.7 Bearing capacity factor N" for piles in
sand (From Berezantsev et 01. 1961 )
Critical depth (Figures 10.8-10.10)
Equation 10.15 suggests that as the pile penetrates
more deeply into the sand the end bearing resistance
will increase with depth. However, field tests have
shown that end bearing resistance does not increase
continually with depth. It seems more logical that end
bearing resistance depends on the mean effective stress
at pile base level rather than just the vertical stress:
o '=1(0 '+20 ,) m 3 v H (10.16)
Since 0H' = Ko 0v' end bearing resistance will then be
affected by the Ko value which forThe Mohr-Coulomb criterion for soils at higher
stress levels often shows some curvature rather than
the straight line assumed. Thus as the stresses at pile
base level increase the <P' value and, hence, the bearing
capacity factor Nq decreases. Arching is also considered
to be a contributory factor. The combined effect
is to obtain decreasing end bearing resistance with
depth.
The simplest way of incorporating this effect into
pile design is to adopt the concept of a critical depth Zc
as shown in Figure 10.8. Even though the vertical
effective stress 0/ increases with depth the end bearing
resistance qb and the skin friction/, are considered
as constant below the critical depth, having the value at
the depth zc' The critical depth has been found to be
shallow for loose sands and deeper for dense sands.
T
critical
depth
-I
Figure 10.8 Critical depth in sands
At the present time, values of this critical depth are
somewhat tentative, the values suggested by Vesic
(1967) and Meyerhof (1976) are given in Figure 10.9.
For the determination of Nq and Zc on Figures 10.7
and 10.9, respectively, the angle of internal friction <P'
should relate to the state of the sand after pile installation
so the values given in Table 10.1 are suggested
(Poulos, 1980).
The initial angle of internal friction <PI', before
installation of the pile, is not an easy parameter to
determine, since sampling disturbance will largely
destroy the initial mineral grain structure, making
laboratory tests meaningless. The <P/ value is usually
obtained from correlations between the SPT 'N' value
or the cone penetrometer qc as illustrated on Figure
10.l0.
Pile Foundations 227
15~------~--------~~-+----~
5~~-----4--------~------~
33 38 43
Angle of internal friction ¢f
Figure 10.9 Values of critical depth
Table 10.1
Values of<P' after installation (From Poulos, 1980)
Values of <P after installation
Requirement
Bored piles Driven piles
Nq
<Pi + 40
-2-
tA' - 3
zc/d
3/44>1' + 10
K,tan8 <PI'
<P I ' is the <P value before installation
Skin friction/. (Figures 10.11 and 10.12)
Assuming effective stresses acting on the pile/soil
surface the unit skin friction/, at a depth z below the top
of a pile is given by:
f =K a 'tan8 s s v (10.16K = coefficient of horizontal stress
0'= angle of friction between the pile surface and the
soil.
400
Since both Ks and tanS will be governed by the
method of installation, and values of these factors may
be difficult to assess separately, a simple approach is to
consider values of the lumped parameter Kstano (cf. f3
for effective stress approach to piles in clay, Equation
10.14). Values of this parameter are given in Figure
10.11 related to the initial angle of internal friction.
These are based on Ks values given by Meyerhof
(1976), the lj> values given in Table 10.1 and assuming
o = 0.75lj>', for a normally consolidated sand. Higher
values may be possible for overconsolidated sands.
1.2~-------------+----~~------~
It has been found that skin friction values also
decrease with depth in a similar fashion to end bearing
resistance so a critical depth Zc approach should be
adopted. Values of Zc can be obtained from Table 10.1
and Figure 10.9.
The total shaft load must then be summated from the
shaft loads Q,), QS2' etc, as illustrated in Figure 10.12.
0.8~-------------+'~------~~--~
0.4 f-------,f-----;~+---__r_'------1
35
Initial angle of internal friction ¢i)'
Figure 10.11 Skin friction parameter K, tanb
(From Poulos. 1980)
40Bored piles in sand
Boring holes in sands loosens an annulus of soil around
the hole and reduces horizontal stresses, so bored piles
constructed in initially dense sands can be expected to
have low load capacity. If jetting techniques are used
then the loosening can be even more severe. Casting
concrete in situ will produce a rough surface but this
effect is diminished by the loosening of the sand.
Poulos (1980) suggests using the methods given for
driven piles but with reduced values of the final angle
of internal friction as given in Table 10.1. Meyerhof
(1976) suggests that for preliminary estimates the base
resistance of a bored pile could be taken as one-third of
the value determined for a driven pile with about onehalf
for the shaft resistance.
Factor of safety
A factor of safety is applied to safeguard against the
uncertainties in the ground conditions and installation
effects, and to limit settlement to a permissible value.
Although piles are often designed by applying a
factor of safety to the ultimate load to obtain a working
load, the over-riding performance criterion for a pile is
that it must not settle more than a permissible amount.
Tomlinson (1987) stated that, from his experience for
piles up to 600 mm diameter, if an overall factor of
safety of 2.5 is adopted to give:
k· I d ultimate load
wor mg oa = factor of safety (10.17)
the settlement of the pile under the working load is
unlikely to exceed 10 mm.
;;,
------------1-- ;;, I
3 • t
Qb (Value at critical depth)
For piles larger than 600 mm diameter, it has been
found that, in clays the two components, shaft resistance
and base resistance are mobilised at different
amounts of settlement. Approximately, the full shaft
resistance is mobilised at a pile head settlement of
about 1- 2% of the pile diameter, whereas to mobilise
the full base resistance the pile must be pushed down
about 10--20% of the diameter. This is illustrated in
Figure 10.13.
\
\
~-
\
\
\
\
\
\
\
\
\
\
\
\
\
\
\
\
\
\
\
\
\
\
I
I
I
I
I
I
I
Base
Load
Working load
SI aft
Load
Load on pile
Total
Load
Figure 10.13 Mobilisation of base and shaft loads
For a typical pile diameter and a permissible settlement
of Pall' it can be seen that when the working load
is applied to obtain this settlement a large proportion
of the shaft resistance is mobilised with only a small
proportion of the base resistance acting.
You might also like
- 10211-TCW-DS-RPT-003 Rev01 Geotechnical Design (Cover Page & Review Sheet)Document78 pages10211-TCW-DS-RPT-003 Rev01 Geotechnical Design (Cover Page & Review Sheet)Sayan MahapatraNo ratings yet
- (XPERTZ) Preboard Exam 1ST HGE Nov 2022Document9 pages(XPERTZ) Preboard Exam 1ST HGE Nov 2022Fely Joy RelatoresNo ratings yet
- Load Carrying Capacity of PilesDocument29 pagesLoad Carrying Capacity of PilesMalik Rizwan100% (1)
- Quick Design Guide For Screw Piles and Helical Anchors Short VErsion1Document13 pagesQuick Design Guide For Screw Piles and Helical Anchors Short VErsion1georgesan777No ratings yet
- Drilling Engineering Problems and Solutions: A Field Guide for Engineers and StudentsFrom EverandDrilling Engineering Problems and Solutions: A Field Guide for Engineers and StudentsRating: 5 out of 5 stars5/5 (1)
- 3Document6 pages3jkhy78150No ratings yet
- Driven Piles in Sand: (Figure 10.7)Document5 pagesDriven Piles in Sand: (Figure 10.7)one engNo ratings yet
- Theory and AppliDocument6 pagesTheory and AppliDeep EngineeringNo ratings yet
- Design of Large Dia Bored PilesDocument37 pagesDesign of Large Dia Bored PilesBalajiNo ratings yet
- MSC Formula SheetDocument19 pagesMSC Formula SheetENgřMuhăɱɱadRiǺzAhɱadNo ratings yet
- 5Document6 pages5jkhy78150No ratings yet
- LECTURE - FoundationsDocument6 pagesLECTURE - FoundationsFazelah YakubNo ratings yet
- Bearing N Settlement 3Document13 pagesBearing N Settlement 3U4rayNo ratings yet
- Desain Pondasi 1Document27 pagesDesain Pondasi 1Hendra CenNo ratings yet
- Casing DesignDocument9 pagesCasing DesignRegian Achmad KalisNo ratings yet
- Uplift Capacity of Piles 6Document3 pagesUplift Capacity of Piles 6nhoniepogiNo ratings yet
- Allowable Bearing PressureDocument2 pagesAllowable Bearing PressureyuegengmingNo ratings yet
- Wk9 Bearing Capacity From Field TestsDocument35 pagesWk9 Bearing Capacity From Field TestsAli Saeed100% (2)
- CE325 - 16 Pile CapacityDocument45 pagesCE325 - 16 Pile CapacityAhmadAliAKbarPhambraNo ratings yet
- Job No. 7: To Determine Job The Bearing Capacity of Soil Through Plate Load Test 7.1objectiveDocument8 pagesJob No. 7: To Determine Job The Bearing Capacity of Soil Through Plate Load Test 7.1objectiveEman ArshadNo ratings yet
- Chapter 13Document40 pagesChapter 13VladSimionNo ratings yet
- Bearing Capacity of Shallow FoundationsDocument15 pagesBearing Capacity of Shallow FoundationsKresno N SoetomoNo ratings yet
- Design of Deep Pile Foundations: Faculty of Civil Engineering and Planning Islamic University of Indonesia, YogyakartaDocument53 pagesDesign of Deep Pile Foundations: Faculty of Civil Engineering and Planning Islamic University of Indonesia, YogyakartaFajar MahendraNo ratings yet
- Base Plate LSD SubramanianDocument20 pagesBase Plate LSD SubramanianShakil AkhterNo ratings yet
- 2.1 Deep Foundation (Pile) PAD-BH-01, PAD-BH-02 and CPPDocument6 pages2.1 Deep Foundation (Pile) PAD-BH-01, PAD-BH-02 and CPPaitzaz561No ratings yet
- Load Tests For Jet Grouting at MacauDocument8 pagesLoad Tests For Jet Grouting at MacauMatteoTrigliaReatoNo ratings yet
- Stone ColumsDocument86 pagesStone Columssharath1199No ratings yet
- Piles and Piling FormulaDocument10 pagesPiles and Piling FormulaSamia H. BhuiyanNo ratings yet
- Design of Plate GirdersDocument109 pagesDesign of Plate GirdersboyzesNo ratings yet
- 2010 ISFOG Perth - Setup of Suction Piles - Colliat ColliardDocument5 pages2010 ISFOG Perth - Setup of Suction Piles - Colliat Colliardjasonwu1115No ratings yet
- Calculation Procedures For Installation of Suction CaissonsDocument34 pagesCalculation Procedures For Installation of Suction Caissonslollyb100% (1)
- FHWA Drilled Shafts Construction Procedures and LRFD Design Methods APP-CDocument14 pagesFHWA Drilled Shafts Construction Procedures and LRFD Design Methods APP-CmalangpeerNo ratings yet
- Chapter 9: Pile Foundations: Civil Engineering Department: Foundation Engineering (ECIV 4052)Document18 pagesChapter 9: Pile Foundations: Civil Engineering Department: Foundation Engineering (ECIV 4052)Niamul IslamNo ratings yet
- Chalk Statement 2004Document4 pagesChalk Statement 2004Toddy SamuelNo ratings yet
- Tower Foundation - Chapter 5Document45 pagesTower Foundation - Chapter 5kayshephNo ratings yet
- A Brief Guide To Design of Bored Piles Under Axial CompressionDocument15 pagesA Brief Guide To Design of Bored Piles Under Axial Compressiondanielsu87No ratings yet
- Driven Piles in Dense SandDocument11 pagesDriven Piles in Dense SandmarcvenzNo ratings yet
- 400x400 Pile Capacity With 6T25 & 12mm LinkDocument9 pages400x400 Pile Capacity With 6T25 & 12mm LinkChan Kin CheungNo ratings yet
- Bifs-: An (OverconsoDocument5 pagesBifs-: An (OverconsoRed OrangeNo ratings yet
- Iih .1 12.5M K 0.6: 0.7. in FactDocument8 pagesIih .1 12.5M K 0.6: 0.7. in FactkevinskevinsNo ratings yet
- Design and Construction of Reinforced Embankments Over Weal FoundationsDocument14 pagesDesign and Construction of Reinforced Embankments Over Weal FoundationsNguyễn Duy PhongNo ratings yet
- Shallow Foundation NotesDocument52 pagesShallow Foundation NotesBAMSNo ratings yet
- Burland and Burbidge 1985Document57 pagesBurland and Burbidge 1985Jawad AbidiNo ratings yet
- 08 - Footings On SandDocument16 pages08 - Footings On SandHoshear Bakr100% (1)
- Design and Testing of Bored Pile Foundation To The 2 Penang Bridge, MalaysiaDocument43 pagesDesign and Testing of Bored Pile Foundation To The 2 Penang Bridge, MalaysiaOsama EL HakimNo ratings yet
- Anchorage SDocument31 pagesAnchorage SDiego Alejandro Flores OrtízNo ratings yet
- CPT For Soft Sediments and Deepwater Investigations: R. Boggess & P.K. RobertsonDocument8 pagesCPT For Soft Sediments and Deepwater Investigations: R. Boggess & P.K. RobertsonMoe Ko KoNo ratings yet
- Numerical Modelling of Tension PilesDocument13 pagesNumerical Modelling of Tension Pilesnidar100% (1)
- Shallow Foundation,,,, PDFDocument48 pagesShallow Foundation,,,, PDFJKDLJSJFLSNo ratings yet
- Oral Question Dubai Municipality G+12 Exam. 1. What Is Story DriftDocument6 pagesOral Question Dubai Municipality G+12 Exam. 1. What Is Story Driftarman malikNo ratings yet
- Oral Question Dubai Municipality G+12 Exam. 1. What Is Story DriftDocument6 pagesOral Question Dubai Municipality G+12 Exam. 1. What Is Story Driftarman malikNo ratings yet
- Bearing Capacity of Mat FoundationDocument6 pagesBearing Capacity of Mat FoundationMike Matshona100% (1)
- Factors That Could Affect The Test Results. The Measured SPT N Value Can Be InfluencedDocument4 pagesFactors That Could Affect The Test Results. The Measured SPT N Value Can Be InfluencedlenanaNo ratings yet
- The Fatigue Strength of Transverse Fillet Welded Joints: A Study of the Influence of Joint GeometryFrom EverandThe Fatigue Strength of Transverse Fillet Welded Joints: A Study of the Influence of Joint GeometryNo ratings yet
- Flexible Glass: Enabling Thin, Lightweight, and Flexible ElectronicsFrom EverandFlexible Glass: Enabling Thin, Lightweight, and Flexible ElectronicsSean M. GarnerNo ratings yet
- Basement WallDocument9 pagesBasement WallPrincess ToumaNo ratings yet
- Jalukbari ..Document35 pagesJalukbari ..RAJAT SHARMANo ratings yet
- Soil Exploration Report-KilpaukDocument13 pagesSoil Exploration Report-KilpaukVasanthakumar100% (1)
- 05-1.5 Diameter Effects On P-Y Curves PDFDocument15 pages05-1.5 Diameter Effects On P-Y Curves PDFHüseyin EkiciNo ratings yet
- Horizontal Vertical Horizontal Moment Node L/C FX KN Fy KN FZ KN MX KNM My KNMDocument7 pagesHorizontal Vertical Horizontal Moment Node L/C FX KN Fy KN FZ KN MX KNM My KNMEr Nilesh GajeraNo ratings yet
- P4S4 - GeotechnicalDocument50 pagesP4S4 - GeotechnicalDoniNo ratings yet
- International CPRF GuidelineDocument17 pagesInternational CPRF GuidelineqsultanNo ratings yet
- Foundation Engineering by Md. Manzur RahmanDocument39 pagesFoundation Engineering by Md. Manzur RahmanSerafinaNo ratings yet
- Pile Capacity For Eccentric Inclined Load in ClayDocument8 pagesPile Capacity For Eccentric Inclined Load in Clayshivarajkumar goudarNo ratings yet
- Wall Footing DesignDocument2 pagesWall Footing DesignYllor Koichi RamosNo ratings yet
- BS 1377 Part 9: 1990 StandardDocument9 pagesBS 1377 Part 9: 1990 StandardDetoned StonedNo ratings yet
- Review of Methods For Estimating Pile CapacityDocument9 pagesReview of Methods For Estimating Pile CapacityEskorbutanoNo ratings yet
- Isolated Footing Design (ACI 318-11) : Footing No. Group ID Foundation Geometry - Length Width ThicknessDocument133 pagesIsolated Footing Design (ACI 318-11) : Footing No. Group ID Foundation Geometry - Length Width ThicknessArnold VercelesNo ratings yet
- Principles of Foundation Engineering 9Th Edition Si Edition Braja M Das Download PDF ChapterDocument51 pagesPrinciples of Foundation Engineering 9Th Edition Si Edition Braja M Das Download PDF Chapterjoanne.tinley843100% (11)
- TOS 1 Unit 3 Transfer of LoadDocument13 pagesTOS 1 Unit 3 Transfer of Loadflower lily100% (1)
- Progressive Failure Analysis of Shallow Foundations On Soils With Strain-Softening BehaviourDocument8 pagesProgressive Failure Analysis of Shallow Foundations On Soils With Strain-Softening BehaviourIonut PatrasNo ratings yet
- Shallow Foundations and Retaining Walls PDFDocument9 pagesShallow Foundations and Retaining Walls PDFRovillene Panangwe100% (1)
- Terzaghi's MethodDocument7 pagesTerzaghi's MethodSaranya ChandruNo ratings yet
- Case Study: Performance of A Geogrid Stabilised Working Platform Constructed Over Extremely Soft Dredged SiltDocument9 pagesCase Study: Performance of A Geogrid Stabilised Working Platform Constructed Over Extremely Soft Dredged SiltBrandon Nova AndlerNo ratings yet
- GEO5 - Software Programs Comply Eurocode7 Bearing Capacity Strip FoundationsDocument12 pagesGEO5 - Software Programs Comply Eurocode7 Bearing Capacity Strip Foundationsk08ivanNo ratings yet
- At 14 1Document5 pagesAt 14 1Icz FuentesNo ratings yet
- Performance of Stone Columns in Soft Clay: Numerical EvaluationDocument11 pagesPerformance of Stone Columns in Soft Clay: Numerical EvaluationPatcharakan HNo ratings yet
- Bearing Capacity of Eccentrically Loaded Surface Foot - 1981 - Soils and FoundatDocument5 pagesBearing Capacity of Eccentrically Loaded Surface Foot - 1981 - Soils and FoundatEdson Orlando Hoyos CeronNo ratings yet
- Trenter2004 - Approaches To The Design of Cantilever Retaining WallsDocument9 pagesTrenter2004 - Approaches To The Design of Cantilever Retaining WallsValerioNo ratings yet
- Geotechnic-JKR ProbeDocument4 pagesGeotechnic-JKR Probeahmad adliNo ratings yet
- PDFDocument31 pagesPDFEko wahyuNo ratings yet
- Ejemplo Cimentación Con EurocódigoDocument7 pagesEjemplo Cimentación Con EurocódigoLeonardo CruzNo ratings yet
- Tema 1 - Resistencia Del Suelo Al CorteDocument220 pagesTema 1 - Resistencia Del Suelo Al CorteIvan Villa AriasNo ratings yet