Professional Documents
Culture Documents
Boolean
Boolean
Uploaded by
12021ps30Original Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Boolean
Boolean
Uploaded by
12021ps30Copyright:
Available Formats
Chapter 3.
Boolean Algebra and Logic Design
Boolean Algebra
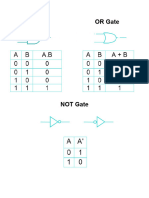
Definition: A two-valued Boolean algebra is defined on a set of 2 elements B = {0,1} with 3 binary operators
OR (+), AND ( • ), and NOT ( ' ).
B B
+ 0 1 0 1 '
0 0 1 0 0 0 0 1
A A A
3.2 Axioms - need no proof. 1 1 1 1 0 1 1 0
1. Closure Property.
The result of each operation is an element of B.
2. Identity Element.
a) 1 for AND because x • 1 = 1 • x = x.
b) 0 for OR because x + 0 = 0 + x = x.
3. Commutative Property. From the symmetry of the tables.
a) x • y = y • x.
b) x + y = y + x.
4. Distributive Property.
a) x • (y + z) = (x • y) + (x • z).
b) x + (y • z) = (x + y) • (x + z).
To show that this is true, we need to show that for any value of binary variables x, y, and z, x • (y + z) will have
the same value as (x • y) + (x • z).
x y z y+ z x( y+ z) xy xz (xy) + (xz)
0 0 0 0 0 0 0 0
0 0 1 1 0 0 0 0
0 1 0 1 0 0 0 0
0 1 1 1 0 0 0 0
1 0 0 0 0 0 0 0
1 0 1 1 1 0 1 1
1 1 0 1 1 1 0 1
1 1 1 1 1 1 1 1
5. Complement Element. For every x ∈ B, there exists a complement element x' ∈ B such that:
a) x + x' = 1 0 + 0' = 0 + 1 = 1 and 1 + 1' = 1 + 0 = 1
b) x • x' = 0 0 • 0' = 0 • 1 = 0 and 1 • 1' = 1 • 0 = 0
6. Cardinality Bound. There are at least 2 elements x, y ∈ B such that x ≠ y. 0 ≠ 1.
Chapter 3. Boolean Algebra and Logic Design
3.3 Basic Theorems - need to be proven.
1. Idempotency. Proof of 1a)
a) x + x = x. x + x = (x + x) • 1 by Axiom 2a
b) x• x = x. = (x + x) (x + x') by Axiom 5a
= x + xx' by Axiom 4b
2. a) x + 1 = 1. =x+0 by Axiom 5b
b) x • 0 = 0. =x by Axiom 2b
3. Absorption. Proof of 3a)
a) yx + x = x yx + x = yx + 1x by Axiom 2a
b) (y + x)x = x = x(y + 1) by Axiom 4a
= x1 by Theorem 2a
4. Involution. =x by Axiom 2a
a) (x')' = x
Proof of 3b)
5. Associative. (y + x)x= xy + xx by Axiom 4a
a) (x + y) + z = x + (y + z) = xy + x by Theorem 1b
b) x (y z) = (x y) z =x by Theorem 3a
Proof of 3b)
x y y+x (y+x) x
0 0 0 0
0 1 1 0
De Morgan's Law.
a) (x + y)' = x' y' 1 0 1 1
b) (x y)' = x' + y' 1 1 1 1
Duality Principle.
This principle states that any algebraic equality derived from these axioms will still be valid whenever the OR and
AND operators, and identity elements 0 and 1, have been interchanged. i.e. changing every OR into AND and vice
versa, and every 0 into 1 and vice versa.
Ex. Theorem 1b) follows from Theorem 1a) by the duality principle.
3.4 Boolean Functions
Boolean functions are formed from binary variables and the Boolean operators AND, OR, and NOT. For a given
value of the variables, the value of the function is either 0 or 1. e.g.
3 AND terms
F1 = x y + x y' z + x' y z
2 litererals 3 litererals
This function equals 1 if:
• x = 1 and y = 1 (doesn't matter what z is)
• x = 1, y = 0, and z = 1
• x = 0, y = 1, and z = 1
otherwise, F1 = 0.
Chapter 3. Boolean Algebra and Logic Design
Boolean functions can also be defined by a truth table:
x y z + x y z' = x y (z + z')
Variable Values Function Values = x y (1)
x y z F1 F1' =xy
0 0 0 0 1
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 0
3.4.1 Complement of a Function
The complement of any function F is F '. Its value can be obtained by interchanging the 0's for 1's and 1's for 0's in
the value of F.
There are two ways to determine the algebraic expression for the complement of a function:
1. Apply the generalized form of De Morgan's Law as many times as necessary.
Ex. F '= (x y + x y' z + x' y z)'
= (x y)' (x y' z)' (x' y z)'
= (x' + y') (x' + y + z') (x + y' + z')
Difficult to see when F ' = 1. Easier to see when F ' = 0. F ' = 0 when each term is 0.
2. Use the duality principle, i.e. interchange the AND and OR operators, and by complementing each literal.
Ex. (x y) ⇒ (x' + y')
(x y' z) ⇒ (x' + y + z')
(x' y z) ⇒ (x + y' + z')
therefore, (x y) + (x y' z) + (x' y z) ⇒ (x' + y') (x' + y + z') (x + y' + z')
The same function can be specified by two or more different algebraic expressions.
3.4.2 Graphic representation
Boolean functions can be expressed graphically by connecting together AND, OR, and NOT operators, as specified
by the algebraic expression that was used to define the function.
Ex. F1 = (x y) + (x y' z) + (x' y z)
x y z
F = xy + xy'z + x'yz
xy
+ xy + xy'z
xy'z + F
xy'
xy'z
F'
x'y
You might also like
- Discrete Math Chapter 6Document11 pagesDiscrete Math Chapter 6kumar_anup1175% (4)
- Sapta Rishi Nadi by BhasinDocument204 pagesSapta Rishi Nadi by BhasinAnonymous jGdHMEODVm100% (4)
- Lec-6-Boolean AlgebraDocument3 pagesLec-6-Boolean AlgebraTonmoy ChowdhuryNo ratings yet
- Boolean Algebra and Logic GateDocument30 pagesBoolean Algebra and Logic Gateهشام المالكيNo ratings yet
- Lec 5Document31 pagesLec 5Ahmet ArabNo ratings yet
- Cse 205: Digital Logic DesignDocument55 pagesCse 205: Digital Logic DesignIFTEKHAR E MAHBUB ZEEONNo ratings yet
- Boolean Algebra and Logic GatesDocument72 pagesBoolean Algebra and Logic GatesSyed Awais AliNo ratings yet
- DSD Boolean Algebra and Logic GatesDocument45 pagesDSD Boolean Algebra and Logic GatesKhaja Mujeebuddin QuadryNo ratings yet
- Lecture 3Document25 pagesLecture 3api-3729886No ratings yet
- Boolean Algebra: Digital CircuitsDocument45 pagesBoolean Algebra: Digital CircuitsPSNo ratings yet
- Boolean Theorem Penned by Faisal HaroonDocument3 pagesBoolean Theorem Penned by Faisal HaroonFaisal HaroonNo ratings yet
- XX XX Xyb Xy: X XX X XX Xyyx Xyyx Xyz Xy XZ X Yz Xyxz XB XBDocument14 pagesXX XX Xyb Xy: X XX X XX Xyyx Xyyx Xyz Xy XZ X Yz Xyxz XB XBsinemNo ratings yet
- EE272 Digital Systems Fall 2019 Instructor: Dr. Aashir WaleedDocument41 pagesEE272 Digital Systems Fall 2019 Instructor: Dr. Aashir Waleedsyed waheedNo ratings yet
- Chapter 2 Boolean Algebra and Logic GatesDocument54 pagesChapter 2 Boolean Algebra and Logic GatesAbaid UllahNo ratings yet
- Lecture 05Document27 pagesLecture 05Sujoy BiswasNo ratings yet
- BRAC University, Spring 2011Document22 pagesBRAC University, Spring 2011Ratul RaihanNo ratings yet
- Boolean Algebra: 1 Aim of ChapterDocument15 pagesBoolean Algebra: 1 Aim of ChapterSama AlqasabyNo ratings yet
- 4b (Digital System) Logic Gates - Boolean ExpressionDocument36 pages4b (Digital System) Logic Gates - Boolean ExpressionSyahmi AkmalNo ratings yet
- CSE204Document5 pagesCSE204Robiul Haque BhuyanNo ratings yet
- 3 - Boolean AlgebraDocument15 pages3 - Boolean AlgebraLingesh K VNo ratings yet
- IDS - Lecture 2&3Document108 pagesIDS - Lecture 2&3PSNo ratings yet
- Boolean Algebra and Logic GateDocument52 pagesBoolean Algebra and Logic Gatejohn andy genoviaNo ratings yet
- Lec2 Logic Gates Chap2Document61 pagesLec2 Logic Gates Chap2asmm.rahamanNo ratings yet
- Chapter 3 LogicDocument44 pagesChapter 3 LogicdukeNo ratings yet
- Boolean AlgebraDocument8 pagesBoolean AlgebraLove Life NckNo ratings yet
- 7 Boolean Algebra PDFDocument20 pages7 Boolean Algebra PDFM R Fajar SetiawanNo ratings yet
- Fpure ch2Document22 pagesFpure ch2Chitra S SNo ratings yet
- Theorems - Boolean AlgebraDocument9 pagesTheorems - Boolean AlgebraAparna JNo ratings yet
- Digital Logic Design I: Boolean Algebra and Logic GateDocument33 pagesDigital Logic Design I: Boolean Algebra and Logic GateMohammad Olid AfzalNo ratings yet
- Boolean Algebra and Logic GatesDocument57 pagesBoolean Algebra and Logic GatesABDULLAH AAMIRNo ratings yet
- Unit - 2: Boolean Algebra and Switching FunctionsDocument19 pagesUnit - 2: Boolean Algebra and Switching FunctionshvrkNo ratings yet
- DLD Lec3Document4 pagesDLD Lec34dham.xiNo ratings yet
- 2 Hyperbolic Functions: ObjectivesDocument22 pages2 Hyperbolic Functions: ObjectivesManibalanNo ratings yet
- Boolean AlgebraDocument20 pagesBoolean Algebrafernando vargasNo ratings yet
- 5b (Digital System) Logic Gates & Boolean ExpressionDocument23 pages5b (Digital System) Logic Gates & Boolean ExpressionLove StrikeNo ratings yet
- Exercise Set - Week 1: Problem 1Document4 pagesExercise Set - Week 1: Problem 1Mark HelouNo ratings yet
- Exercise Sheet 4Document4 pagesExercise Sheet 4Đỗ Xuân ViệtNo ratings yet
- Chapter 2Document46 pagesChapter 2Gilbert SigalaNo ratings yet
- Boolean Algebra & Basic DefinitionDocument26 pagesBoolean Algebra & Basic DefinitionVines 747No ratings yet
- MA1505 1920S1 Part I Chapter 1Document19 pagesMA1505 1920S1 Part I Chapter 1Jaehun JeongNo ratings yet
- 5b (Digital System) Logic Gates & Boolean Expression - AminDocument29 pages5b (Digital System) Logic Gates & Boolean Expression - AminHilmyZulkifliNo ratings yet
- EE/CE 6301: Advanced Digital LogicDocument20 pagesEE/CE 6301: Advanced Digital LogicspoortipNo ratings yet
- BooleanAlgebra IDocument15 pagesBooleanAlgebra IAmitava SarderNo ratings yet
- Đề thi GT1 MI1016 CK 20221 aThu EDocument1 pageĐề thi GT1 MI1016 CK 20221 aThu Eanloll812No ratings yet
- Closure W.R.T. The Operator + ( ) 2. Associative W.R.T. + ( ) 3. Commutative W.R.T. + ( )Document8 pagesClosure W.R.T. The Operator + ( ) 2. Associative W.R.T. + ( ) 3. Commutative W.R.T. + ( )Arga SimanjuntakNo ratings yet
- CH 02Document63 pagesCH 02munzarinNo ratings yet
- Lecture 6Document19 pagesLecture 6muktikantaNo ratings yet
- Quarter 4 - Theorems Boolean AlgebraDocument30 pagesQuarter 4 - Theorems Boolean AlgebraOrder Sa shopeeNo ratings yet
- The Most Common Postulates Used To Formulate Various Algebraic Structures AreDocument46 pagesThe Most Common Postulates Used To Formulate Various Algebraic Structures AreAdari G V Chiranjeevi ACOENo ratings yet
- Nama: Desak Putu Sri Wulandari NIM: 1908561019 Kelas: A Prodi: Teknik InformatikaDocument5 pagesNama: Desak Putu Sri Wulandari NIM: 1908561019 Kelas: A Prodi: Teknik InformatikaDesak WulandariNo ratings yet
- Mata Kuliah: Arsitektur Dan Sistem Komputer Kode Mata Kuliah/Sks: Ti2133 / 3 Sks Kurikulum: 2017 Versi: 0.0Document28 pagesMata Kuliah: Arsitektur Dan Sistem Komputer Kode Mata Kuliah/Sks: Ti2133 / 3 Sks Kurikulum: 2017 Versi: 0.0Willyam SaputraNo ratings yet
- Two - Valued - Boolean AlgebraDocument8 pagesTwo - Valued - Boolean AlgebraAparna JNo ratings yet
- T4 Multivariable CalculusDocument1 pageT4 Multivariable CalculusDeepak JhaNo ratings yet
- Digital Logic Design: Lecture# 5 and 6 Boolean Algebra and Logic GatesDocument31 pagesDigital Logic Design: Lecture# 5 and 6 Boolean Algebra and Logic Gatesbilal buttNo ratings yet
- Bayan University of Science and Technology Collage of EngineeringDocument27 pagesBayan University of Science and Technology Collage of EngineeringOmur NoorNo ratings yet
- 2 Boolean Algebra and Logic SimplificationDocument73 pages2 Boolean Algebra and Logic SimplificationBiniam TeferiNo ratings yet
- Week 3 - Module 3 Boolean AlgebraDocument5 pagesWeek 3 - Module 3 Boolean AlgebraBen GwenNo ratings yet
- Boolean Algebra & Logic GatesDocument45 pagesBoolean Algebra & Logic Gateszeeshan jamilNo ratings yet
- CSEE 3827: Fundamentals of Computer Systems, Spring 2021: Prof. Dan Rubenstein (Danr@cs - Columbia.edu)Document54 pagesCSEE 3827: Fundamentals of Computer Systems, Spring 2021: Prof. Dan Rubenstein (Danr@cs - Columbia.edu)Stephen ChoNo ratings yet
- Factoring and Algebra - A Selection of Classic Mathematical Articles Containing Examples and Exercises on the Subject of Algebra (Mathematics Series)From EverandFactoring and Algebra - A Selection of Classic Mathematical Articles Containing Examples and Exercises on the Subject of Algebra (Mathematics Series)No ratings yet
- Transformation of Axes (Geometry) Mathematics Question BankFrom EverandTransformation of Axes (Geometry) Mathematics Question BankRating: 3 out of 5 stars3/5 (1)
- Lec32 Better Spoken English by Shreesh ChaudharyDocument23 pagesLec32 Better Spoken English by Shreesh ChaudharyYasir Mohib100% (1)
- EU New MDR White Paper EMERGODocument28 pagesEU New MDR White Paper EMERGOFrancisco100% (2)
- Chapter 13 Building Information SystemsDocument17 pagesChapter 13 Building Information SystemsLan Anh100% (1)
- College Test DescriptionDocument54 pagesCollege Test DescriptionKleven Carl GindapNo ratings yet
- Energy Meter Reading Protocol AND Calibration Protocol VTEMS11-VT11Document15 pagesEnergy Meter Reading Protocol AND Calibration Protocol VTEMS11-VT11Narender SaineniNo ratings yet
- Premnaths Resume at B.Tech (CSE) 1+ ExpDocument4 pagesPremnaths Resume at B.Tech (CSE) 1+ ExpPrem Nath RNo ratings yet
- Pkpadmin-13 RonzinoDocument13 pagesPkpadmin-13 RonzinoLaia Brugat LuqueNo ratings yet
- Ieee 1609Document3 pagesIeee 1609N Cholis BsyNo ratings yet
- Pre Calculus MODULE 4 (With Key Answers)Document16 pagesPre Calculus MODULE 4 (With Key Answers)KFP[SSRB]しゃらいんNo ratings yet
- Strategic PlanningDocument37 pagesStrategic Planninganshul_4_92No ratings yet
- A Critique of Rawls' Original PositionDocument6 pagesA Critique of Rawls' Original PositionChris StensrudNo ratings yet
- InglesDocument7 pagesInglesMarcos RiveraNo ratings yet
- An Introduction To The Criticism On Sustainable DevelopmentDocument51 pagesAn Introduction To The Criticism On Sustainable DevelopmentJesan AlduesoNo ratings yet
- Inequality and Poverty - A Short Critical Introduction PDFDocument92 pagesInequality and Poverty - A Short Critical Introduction PDFDrMladNo ratings yet
- Study On The Rapid Method To Predict Longevity of Controlled Release FertilizerDocument6 pagesStudy On The Rapid Method To Predict Longevity of Controlled Release FertilizerMurat ÖztürkNo ratings yet
- 362 - Provisional Second Allotment List For LH KCHR Nad LH KHR 2019-20Document2 pages362 - Provisional Second Allotment List For LH KCHR Nad LH KHR 2019-20Samparn PatraNo ratings yet
- Overview Manajemen Strategik 19 Des 2018Document56 pagesOverview Manajemen Strategik 19 Des 2018atikaNo ratings yet
- Frederick Cooper, Work, Class and Empire: An African Historian's Retrospective On E. P. Thompson', Social History 20, No. 2 (1995) : 235-41.Document8 pagesFrederick Cooper, Work, Class and Empire: An African Historian's Retrospective On E. P. Thompson', Social History 20, No. 2 (1995) : 235-41.OSGuinea100% (1)
- Epoch-Modeling and Simulation of An AllDocument40 pagesEpoch-Modeling and Simulation of An Allraducu2009No ratings yet
- Load Balancing: Ranjan Kumar Mondal, Payel Ray, Debabrata SarddarDocument21 pagesLoad Balancing: Ranjan Kumar Mondal, Payel Ray, Debabrata Sarddarযা ইচ্ছে তাইNo ratings yet
- CH 1 Examplar SolutionDocument30 pagesCH 1 Examplar Solution13. Dev Pratap Singh Rathore, 10th BNo ratings yet
- Excavaten Work PermitDocument1 pageExcavaten Work Permitasem sawalmehNo ratings yet
- Example Affidavit - Surveillance Generated Search WarrantDocument10 pagesExample Affidavit - Surveillance Generated Search WarrantShawn Freeman100% (2)
- Designing Urban Space To Achieve Spaces of Real Life For Marginal AreaDocument13 pagesDesigning Urban Space To Achieve Spaces of Real Life For Marginal AreaAlbertNo ratings yet
- English1 Q3 Mod4H DiscussingIllustratingandDramatizingSpecificEvents V1.2Document20 pagesEnglish1 Q3 Mod4H DiscussingIllustratingandDramatizingSpecificEvents V1.2Jesieca BulauanNo ratings yet
- Texas Coastal Resiliency Master PlanDocument208 pagesTexas Coastal Resiliency Master PlanHouston ChronicleNo ratings yet
- Ricoh Error CodesDocument5 pagesRicoh Error CodesjluisteixeiraNo ratings yet
- Data Flow Diagram Level 2Document50 pagesData Flow Diagram Level 2Jade QueenNo ratings yet
- CRC Understanding Digital Image Processing 1138566845 PDFDocument375 pagesCRC Understanding Digital Image Processing 1138566845 PDFWang Chen Yu100% (2)