Professional Documents
Culture Documents
Statistics and Probability Finals Reviewer
Statistics and Probability Finals Reviewer
Uploaded by
Janelle Araña0 ratings0% found this document useful (0 votes)
6 views2 pagesThis document discusses key concepts related to the normal distribution:
1. It defines common probability notation used under the normal curve, such as P(z<a) and P(a<z<b), and explains what these represent.
2. It provides properties and characteristics of the normal distribution, such as its symmetrical bell shape and areas under the curve corresponding to probability.
3. It gives examples of how to calculate z-scores, find probabilities, and solve word problems involving the normal distribution, like finding percentiles from a normal curve.
Original Description:
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentThis document discusses key concepts related to the normal distribution:
1. It defines common probability notation used under the normal curve, such as P(z<a) and P(a<z<b), and explains what these represent.
2. It provides properties and characteristics of the normal distribution, such as its symmetrical bell shape and areas under the curve corresponding to probability.
3. It gives examples of how to calculate z-scores, find probabilities, and solve word problems involving the normal distribution, like finding percentiles from a normal curve.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
Download as pdf or txt
0 ratings0% found this document useful (0 votes)
6 views2 pagesStatistics and Probability Finals Reviewer
Statistics and Probability Finals Reviewer
Uploaded by
Janelle ArañaThis document discusses key concepts related to the normal distribution:
1. It defines common probability notation used under the normal curve, such as P(z<a) and P(a<z<b), and explains what these represent.
2. It provides properties and characteristics of the normal distribution, such as its symmetrical bell shape and areas under the curve corresponding to probability.
3. It gives examples of how to calculate z-scores, find probabilities, and solve word problems involving the normal distribution, like finding percentiles from a normal curve.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
Download as pdf or txt
You are on page 1of 2
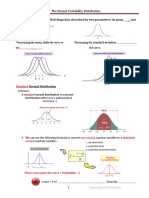
STATISTICS AND PROBABILITY FINALS CASE I P ( z < a) this notation represents the • The number of STANDARD
REVIEWER idea stating the probability that the z-value is DEVIATION
below a, less than a, to the left of a, at most a • A raw score (X) is away from the mean
CASE II P ( z> a) this notation represents the RAW SCORE
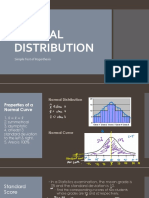
NORMAL DISTRIBUTION
idea stating the probability that the z-value is
above a, greater than a, to the right of a, at least a • The actual data value
a.k.a GAUSSIAN DISTRIBUTION
-NORMAL CURVE OR BELL CURVE CASE III P (a < z < b) this notation represents
the idea stating the probability that the z-value is Given a normal random variable X with mean (μ)
PROPERTIES OF NORMAL between a and b, above a and b, between a and b and standrad deviation (σ ), each value of x of the
DISTRIBUTION variable can be transformed into z-scores using
CASE IV P (a > z > b) = 0 this notation the formula,
1. The graph is a continuous curve and has represents the idea stating the probability that the
a domain -∞ < X < ∞. z-value is less than a but greater than b, below a z = x− μ
2. 2. The graph is asymptotic to the x-axis. but above b σ
The value of the variable gets closer and
closer but will never be equal to 0. This notation indicates that a z-value is equal to where z = z- score or standard score
3. The highest point on the curve occurs at exactly one point on the curve. With that single x = observed value
x = μ (mean). point, a line can be drawn signifying the μ = mean
4. The curve is symmetrical about the probability can be below or above it. That is why, = standard deviation
mean. for a z-value to be exactly equal to a value its
probability is equal to 0 The area of the region under the normal
5. The total area in the normal distribution
curve represents the probability or percentage
under the curve is equal to 1.
or proportion of a given measurement value.
6. In general, the graph of a normal
distribution is a bell-shaped curve with ACTIVITY ACTIVITY
two inflection points.
1. Find the proportion of the area between z 1. In Mrs. Shirley’s science class, a student
7. Every normal curve corresponds to the
= -1.25 and 2.19, this can be expressed as gained a score of 46. What is the z-value
“empirical rule” (also called the 68 - 95 -
P (-1.25 < Z < 2.19), read as the of hisscore if test result has population
99.7% rule)
probability that Z is greater than -1.25 but mean 45 with standard deviation of 2?
PROBABILITY NOTATION UNDER less than 2.19.
NORMAL CURVE 2. Compute the probability using the
standard normal curve.
• are commonly used to express a lengthy a. P(Z < 1.67) = ______________ 2. Leslie got a score of 68 in an
idea into symbols concerning the normal b. P (-2 < z <1) = ______________ examination she participated. What is
curve. c. P (z > -1.5) = ______________ the corresponding z-value of her score if
• The probability of Z having a value that d. P (z > 3) = ______________ the result has mean = 75 and standard
is area under the curve.
deviation= 5
Z- SCORE
• a.k.a STANDARD SCORE
3. A random variable X has a mean of 6 • any set of measurements which Step 4: Get the average of the two z-score
and a standard deviation of 2. Find the may be arranged in ascending or values.
corresponding z-score for x = 11. descending order. ÿ = 1.28 + 1.292= 1.285
• also a measure of relative
standing and The 90th percentile is z=1.285
4. The scores in the summative test of 11-
STEM B are normally distributed with • a descriptive measure of the
a mean of 65 and a standard deviation of relationship of data to the rest of the
SAMPLING
12. Find the probability that some measurements.
students got a score below 40. • The selection of a subject in a
population in order to represent the
EXAMPLE: whole population..
Find the 90th percentile of a normal curve. • a group containing elements of anything
APPLICATIONS OF THE NORMAL
you want to study, such as objects,
DISTRIBUTION (WORD PROBLEMS) Solution: events, organizations, countries, species,
1. Suppose the current annual salary of Step 1: Rewrite the given percentile rank as organisms, etc.
all teachers in the United States have probability. • population is BIGGER THAN sample
a normal distribution with a mean of
90th percentile in probability is 90% or
51000 dollars and a standard 0.90 in decimal form.
deviation of 6000 dollars. Find the
probability that the annual salary of Step 2: Draw the Normal Curve.
a randomly selected teacher would In the given example, we must locate the area
be between 42000 and 65000. which is NOT GREATER than a certain point. It
2. The life span of scientific calculator means that we have to find a value of z at this
has a normal distribution with a point. The probability is 0.90, meaning the area
mean of 58 months and a standard bounded by the curve is 0.90. Given that the
deviation of 10 months. The probability below z equals 0 is 0.50 then we just
company gives a warranty of 36 add 0.40 to make it 0.90.
months to replace any defective Step 3: Find the z-score value in the adopted
calculator with a new one. Suppose z-score table.
the company makes 1 million
calculators per year, how many We must find the area equal to 0.40. If there is
no exact area equal to 0.40, then get two
calculators may be replaced?
values above and below of 0.40 and interpolate.
In this case, the closest values are:
PERCENTILE
0.3997 → z = 1.28
0.4015 → z = 1.29
You might also like
- The Art and Science of Social Research PDFDocument736 pagesThe Art and Science of Social Research PDFDaniel Vazquez88% (16)
- Statistics Modules 8-11statistics Modules 8-11statistics Modules 8-11statistics Modules 8-11statistics Modules 8-11Document113 pagesStatistics Modules 8-11statistics Modules 8-11statistics Modules 8-11statistics Modules 8-11statistics Modules 8-11Karl Wilson GonzalesNo ratings yet
- Business Analyst Master's Program - Simplilearn - v3Document24 pagesBusiness Analyst Master's Program - Simplilearn - v3Pradeep JNA75% (4)
- Normal Distribution or Normal CurveDocument6 pagesNormal Distribution or Normal CurveJhun francis BisaNo ratings yet
- Stat and Prob - Q3 Week 5 - Mod5Document17 pagesStat and Prob - Q3 Week 5 - Mod5JessicaNo ratings yet
- Normal DistributionDocument32 pagesNormal Distributionmariannchello123No ratings yet
- CHAPTER 2 Normal DistributionDocument55 pagesCHAPTER 2 Normal DistributionMissEu Ferrer MontericzNo ratings yet
- Week 5: Statistics and ProbabilityDocument21 pagesWeek 5: Statistics and ProbabilityKriza mae alvarezNo ratings yet
- 07 Z-ScoreDocument17 pages07 Z-ScoreVASQUEZ SYRANo ratings yet
- Ormal Istribution: f (x) = e σ ; α= x−μ σ x<Document1 pageOrmal Istribution: f (x) = e σ ; α= x−μ σ x<Erwin BulahaoNo ratings yet
- Chapter 2 Normal DistributionDocument31 pagesChapter 2 Normal DistributionJustin BorjaNo ratings yet
- Statistics and Probability 11Document12 pagesStatistics and Probability 11joshcaleboliverosNo ratings yet
- Grade11 Statistics and Probabilty - Module 3Document5 pagesGrade11 Statistics and Probabilty - Module 3Erickson SongcalNo ratings yet
- Understanding The Z - Scores C2 Lesson 2Document7 pagesUnderstanding The Z - Scores C2 Lesson 2CHARLYN JOY SUMALINOGNo ratings yet
- Converting Z ScoresDocument14 pagesConverting Z ScoresMary Jane Duma-ogNo ratings yet
- STAT 1013 Statistics: Week 11Document50 pagesSTAT 1013 Statistics: Week 11Angelo ValdezNo ratings yet
- Areas Under A Normal DisctributionDocument16 pagesAreas Under A Normal Disctributionvincent.dequit77No ratings yet
- STATSDocument4 pagesSTATSdennisalejaga08No ratings yet
- PO 1-09 Normal Distribution PDFDocument4 pagesPO 1-09 Normal Distribution PDFshynaNo ratings yet
- Z-Test: Variance of A Dicrete Probability DistributionDocument13 pagesZ-Test: Variance of A Dicrete Probability Distribution11 STEM 4 - CORTAZ,TRISHA MAE ANTHONYNo ratings yet
- Week 2 - Probability and Normal DistributionDocument30 pagesWeek 2 - Probability and Normal DistributionAbrashiNo ratings yet
- Statistics and Probability Quarter 3 Week 4 PDFDocument26 pagesStatistics and Probability Quarter 3 Week 4 PDFSam OxfordNo ratings yet
- StatProb Lesson 45Document36 pagesStatProb Lesson 45Lee HeeseungNo ratings yet
- Normal DistributionDocument35 pagesNormal DistributionEvelyn VelascoNo ratings yet
- Gerstman PP07Document35 pagesGerstman PP07narayanNo ratings yet
- Chapter6 IPS14eDocument23 pagesChapter6 IPS14eSamantha Cruz BlancoNo ratings yet
- Probability and StatisticsDocument27 pagesProbability and Statisticscrazytrabzonlu28No ratings yet
- Lfstat3e PPT 06 RevDocument44 pagesLfstat3e PPT 06 RevmarifeNo ratings yet
- Normal DistributionDocument24 pagesNormal DistributionPam FajardoNo ratings yet
- Topic 5-20200317101441 PDFDocument15 pagesTopic 5-20200317101441 PDFHaffidzry HuzraynNo ratings yet
- Lesson 7Document48 pagesLesson 7Rengeline LucasNo ratings yet
- Stat and Prob Q3 Week 5 Mod5 Carla CatherineDocument20 pagesStat and Prob Q3 Week 5 Mod5 Carla CatherineCharlene Binasahan100% (2)
- The Normal DistributionDocument47 pagesThe Normal DistributionAllen Kurt RamosNo ratings yet
- Inferential Testing: Tests of DifferenceDocument7 pagesInferential Testing: Tests of DifferenceKezia MadeloNo ratings yet
- Gerstman PP07Document35 pagesGerstman PP07Kent gonzagaNo ratings yet
- Normal DistributionDocument46 pagesNormal DistributionRain ReevNo ratings yet
- MethDocument6 pagesMethdelinftwNo ratings yet
- Normal DistributionDocument9 pagesNormal DistributionFilipa EguavoenNo ratings yet
- Continuous Probability Distribution-FinalDocument56 pagesContinuous Probability Distribution-Finalshashank vyas100% (1)
- Normal DistributionDocument26 pagesNormal DistributionnorikivesNo ratings yet
- Lesson 6:: Understanding The Z-ScoresDocument52 pagesLesson 6:: Understanding The Z-ScoresTrice DomingoNo ratings yet
- Module 5Document61 pagesModule 5HarijaNo ratings yet
- Normal DistributionDocument23 pagesNormal Distributionkoreaneminem2No ratings yet
- 2 Normal DistributionDocument39 pages2 Normal DistributionDANELYN PINGKIANNo ratings yet
- CHAPTER 4 Normal Distribution Z-ScoresDocument33 pagesCHAPTER 4 Normal Distribution Z-Scoresapi-3729261100% (7)
- Normal Distribution PPTDocument20 pagesNormal Distribution PPTEcho AlbertoNo ratings yet
- Normal Distribution: Simple Test of HypothesisDocument13 pagesNormal Distribution: Simple Test of Hypothesisednalyn ladiaoNo ratings yet
- Group 1 Report (1) (Autosaved)Document51 pagesGroup 1 Report (1) (Autosaved)Rheanna Nogales BanguilanNo ratings yet
- Lesson 3. Continuous Probability DistributionDocument18 pagesLesson 3. Continuous Probability DistributionCELESTIAL TONGOL VALDEVIESONo ratings yet
- 2 3a. Normal Distribution and Sampling and Sampling DistributionsDocument64 pages2 3a. Normal Distribution and Sampling and Sampling DistributionsMavic Montaña75% (4)
- Normal Probability DistributionsDocument61 pagesNormal Probability DistributionsJuliana Marie RarasNo ratings yet
- Normal Distribution Part 2Document71 pagesNormal Distribution Part 2johndeocampo14No ratings yet
- Robability Istribution: Poona College of Pharmacy, Centre of Advanced Research in Pharmaceutical SciencesDocument23 pagesRobability Istribution: Poona College of Pharmacy, Centre of Advanced Research in Pharmaceutical SciencesDebjani BaidyaNo ratings yet
- Chapter 5Document54 pagesChapter 5KarliNo ratings yet
- Identifying Regions Under Normal Curve Correponds To DifferentDocument32 pagesIdentifying Regions Under Normal Curve Correponds To DifferentJiro Alejo TutopNo ratings yet
- Module 1C Normal DistributionDocument33 pagesModule 1C Normal DistributionKim IgnacioNo ratings yet
- Lesson 2.2 - Understanding The Z-ScoreDocument24 pagesLesson 2.2 - Understanding The Z-ScoreHayashida KunNo ratings yet
- Notes No. 5 For 11 e Understanding Z ScoresDocument5 pagesNotes No. 5 For 11 e Understanding Z Scoresnikkigabanto.24No ratings yet
- Normal DistributionDocument50 pagesNormal Distributionscropian 9997No ratings yet
- Math 002 Module No.2Document13 pagesMath 002 Module No.2abejero22212550mNo ratings yet
- Normal Probability Distribution IDocument24 pagesNormal Probability Distribution ISafia tahirNo ratings yet
- Chapter 3 BSMTDocument5 pagesChapter 3 BSMTjmar0% (1)
- 2019 - Van Aert - Publication Bias Examined in Meta-Analyses From Psychology and Medicine - A Meta-Meta-AnalysisDocument32 pages2019 - Van Aert - Publication Bias Examined in Meta-Analyses From Psychology and Medicine - A Meta-Meta-AnalysisLim Kok PingNo ratings yet
- SCMH 2.7.2 Variation Sensitivity Analysis Overview Dated 1OCT2020Document41 pagesSCMH 2.7.2 Variation Sensitivity Analysis Overview Dated 1OCT2020Alberto Sánchez RamírezNo ratings yet
- Quantech Investments Smart BetaDocument16 pagesQuantech Investments Smart BetaAnthony Fj Garner100% (1)
- 2014-3-Pen-Jit Sin - Marking Scheme No Working/Answer Partial Marks Total Marks 6Document6 pages2014-3-Pen-Jit Sin - Marking Scheme No Working/Answer Partial Marks Total Marks 6Norbert LimNo ratings yet
- Sheet 1 Applied PDFDocument7 pagesSheet 1 Applied PDFyehyaNo ratings yet
- Punjab Technical University: Marketing ResearchDocument2 pagesPunjab Technical University: Marketing ResearchAmuliya VSNo ratings yet
- Lampiran 24 Hasil Analisis Data Uji Post Hoc (Uji Tukey HSD Dan Uji LSD)Document6 pagesLampiran 24 Hasil Analisis Data Uji Post Hoc (Uji Tukey HSD Dan Uji LSD)Aas NuraisahNo ratings yet
- Information Theory: A Tutorial IntroductionDocument23 pagesInformation Theory: A Tutorial Introductiongerardlindsey60No ratings yet
- 2012-01-02 203611 Answers2Document9 pages2012-01-02 203611 Answers2medeepikaNo ratings yet
- Supervised Learning (Classification and Regression)Document14 pagesSupervised Learning (Classification and Regression)shreya sarkarNo ratings yet
- Heavy-Tailed DistributionDocument7 pagesHeavy-Tailed Distributionchuck333No ratings yet
- Lecture - ECON 7223 - 2Document23 pagesLecture - ECON 7223 - 2Trang DangNo ratings yet
- Basic Statistics Lecture NotesDocument6 pagesBasic Statistics Lecture NotesKit LaraNo ratings yet
- USP Dissolution StudiesDocument18 pagesUSP Dissolution StudiesSayeeda MohammedNo ratings yet
- Muhammad Reza Chandra Kusuma - 20180913150015 - TP4-W6-S7-R0 - 2140071320Document5 pagesMuhammad Reza Chandra Kusuma - 20180913150015 - TP4-W6-S7-R0 - 2140071320m reza chandra kNo ratings yet
- Designing A Better Paper Helicopter: Using Response Surface MethodologyDocument14 pagesDesigning A Better Paper Helicopter: Using Response Surface MethodologyJay PanchalNo ratings yet
- CompleteDocument10 pagesCompleteJomara RossellNo ratings yet
- Module 2-Marketing ResearchDocument8 pagesModule 2-Marketing ResearchJo MalaluanNo ratings yet
- MBA Version ADocument13 pagesMBA Version AsurabhiNo ratings yet
- The Relationship Between Innovations and Quality Management SystemDocument7 pagesThe Relationship Between Innovations and Quality Management SystemVIJAY KUMARNo ratings yet
- Math CurriculumDocument13 pagesMath CurriculumLorraine SabbaghNo ratings yet
- Chapter 1 - Introduction To Statistics - Part 1Document20 pagesChapter 1 - Introduction To Statistics - Part 1Faten ZaraNo ratings yet
- Department of Industrial Engineering and Operations ResearchDocument11 pagesDepartment of Industrial Engineering and Operations ResearchCeceNo ratings yet
- Applied Statistics in Business and Economics 4Th Edition Doane Test Bank Full Chapter PDFDocument18 pagesApplied Statistics in Business and Economics 4Th Edition Doane Test Bank Full Chapter PDFtess.lechner250100% (21)
- Uji Normalitas Dan HomogenitasDocument18 pagesUji Normalitas Dan HomogenitasKelana FactoryNo ratings yet
- Entropy and Kullback-Leibler DivergenceDocument5 pagesEntropy and Kullback-Leibler DivergenceMuhammad Abdul JabbarNo ratings yet
- Analysis of Selected Crime Data in NigeriaDocument9 pagesAnalysis of Selected Crime Data in Nigeriaekerette andrewNo ratings yet