Question 1: Functions and continuity.

(15marks)

1.1) Prove that the function is continuous at points 2 and 3. (2.5marks)

{
√ x +2 x <2
f (x)= x 2 − 2 2≤ x ≤
2 x +5 x ≥ 3
1.2) Verify that the intermediate value theorem applies to the indicated interval and
find the value of ‘c’ guaranteed by the theorem. (2.5marks)
2
f (x)=x + 4 x − 5[0 ,2] f (c )=0
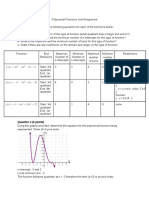
1.3) Considering the function below, analyze the function by drawing its variation
table and graph. (5marks)
2
g(x )=
(x −1)(x −3)
1.4) Evaluate the limit. (5marks)
1
( x+1) 2 − 3
lim
x →2 x −2
Question 2: Sequences and series. (15marks)

sin n
2.1) Use the squeeze theorem to show that lim =0 (2marks)
n→∞ n

2.2) Determine whether the sequences below converge or diverge; if they converge,
compute the limits. (2 x 2.5marks)
∞
2.2A) { √ n+ 47 − √ n }n=0

{ }
∞
n+ 47
2.2B)
√n2 +3 n n=0

2.3) Prove that the recursive sequence is convergent and give the limit of
convergence.a 1=0 an +1=√ 6+a n n≥ 1 (3marks)

2.4) Determine if the series converges or diverges. (3marks)

∞
5 n+3
a n= ∑
n=1 7 n −4

∞
n
2.5) Show that the series diverges ∑ n+1 (2marks)
n =1

Question 3: Real Numbers and Topologies. (10marks)

Let x ℰ ℝ , S={ x∨x 2 >3 } ∧T ={ x∨x 2< 9 } . Let F=( S ∪ T )C , where AC represents the
complement of the set A.
3.1) Define the set F. (2marks)
3.2) Define the boundary,interior, exterior, and closure of F. (3marks)
3.3) Determine the minimum,maximum, supreme, and infimum of the set
S= {Xℰ ℝ |X2>3}if they exist,and justify your answers. (3marks)
3.4) Proof that for any set S, the closure of S is closed. (2marks)