Absolute Value Inequalities

CA1SE 1:

CASE 2:

CASE 3:

The absolute value of any number is either zero (0) or positive which can never be less
than or equal to a negative number.
The answer to this case is always no solution.

CASE 4:

The absolute value of any number is either zero (0) or positive. It makes sense that it must
always be greater than any negative number.

The answer to this case is always all real numbers.

1Page Jafar M.Teli

 Examples of How to Solve Absolute Value Inequalities

Example 1: Solve the absolute value inequality.

This is a “less than” absolute value inequality which is an example of case 1. Get rid of the
absolute value symbol by applying the rule. Then solve the linear inequality that arises.

The goal is to isolate the variable “x” in the middle. To do that, we subtract the left, middle
and right parts of the inequality by 6.

The answer in the form of the inequality symbol states that the solutions are all the values
of x between −8 and −4 but not including −8 and −4 themselves.

We can also write the answer in interval notation using a parenthesis to denote
that −8 and −4 are not part of the solutions.

Or, write the answer on a number line where we use open circles to exclude −8 and −4 from
the solution.

Example 2: Solve the absolute value inequality.

This is a “less than or equal to” absolute value inequality which still falls under case 1.

Clear out the absolute value symbol using the rule and solve the linear inequality.

Isolate the variable “x” in the middle by adding all sides by 6 and then dividing
by 3 (coefficient of x).

2Page Jafar M.Teli

The inequality symbol suggests that the solution are all values of x between −3 and 7, and
also including the endpoints −3 and 7. We include the endpoints because we are using the
symbol “≤“.

To write the answer in interval notation, we will utilize the square brackets instead of the
regular parenthesis to denote that −3 and 7 are part of the solution.

And finally, we will use closed or shaded circles to show that −3 and 7 are included.

Example 3: Solve the absolute value inequality .

Example of a “greater than” absolute value inequality which is an example of case 2.

Let’s eliminate the absolute value expression using the rule below.

As you can see, we are solving two separate linear inequalities.

or

3Page Jafar M.Teli

In interval notation, the word “or” is replaced by the symbol “\cup∪” to mean “union“. The
union of sets means that we are putting together the non-overlapping elements of two or
more sets of solutions.

The answer in interval notation makes more sense if you see how it looks on the number
line. In case 2, the arrows will always be in opposite directions. The open circles imply
that −3 and 7 are not included in the solutions which are the consequence of the symbol “>“.

Example 4: Solve the absolute value inequality.

Break this up into two linear inequalities, and then solve each separately.

Here’s the rule for case 2.

Here’s the solution.

4Page Jafar M.Teli

 Or for the interval solution, we use the square brackets to include −2 and 3 in the

The shaded or closed circles signify that −2 and 3 are part of the solution. In case 2, the
arrows will always point to opposite directions.

Evaluate all values of x into the function y =∣x∣

To get the corresponding y-values.

Notice that the graph has a low point determined by the middle x-value which is the x-
coordinate of the vertex itself, i.e. (0,0).

5Page Jafar M.Teli

Example 5: Solve the absolute value inequities.
1.

2.

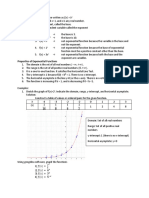
Example 6: Graph the absolute value function below using the table of values.

The first step is to find the x-coordinate of the vertex which will serve as the center
point in the table of values of x.

Plot the points on the xy-plane and connect the dots with a straight edge. If you get it
right, you should have something similar below. As you can see, the low point of the
graph is the vertex located at (2, 0).

6Page Jafar M.Teli

Example 7: Graph the absolute value function below using the table of values.

Features (of parent Symmetric:

function): about x = 0
unless domain is
• Domain: All Real’s (- altered
∞,∞)
Unless domain is altered.
x-intercept:
• Range: [0,∞)
intersects x-
axis at (0, 0)
• increasing (0, ∞) unless domain is
• decreasing (-∞,0) altered

• positive (-∞, 0) U (0, y-intercept:

-∞) intersects y-
axis at (0, 0)
• absolute/relative unless domain is
min is 0 altered
• no absolute max (graph
→ ∞) Vertex:
the point (0,0)
• end behavior unless domain is
altered
f (x) → +∞, as x → +∞
f (x) → +∞, as x → -∞

7Page Jafar M.Teli

Our original definition of Absolute Value: Piecewise definition of Absolute value
( y = | x | ):

8Page Jafar M.Teli