I.

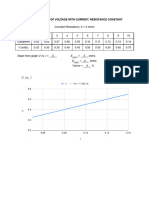
VARIATION OF VOLTAGE WITH CURRENT, RESISTANCE CONSTANT

Constant Resistance, 𝑅 = 5 ohms

TRIAL 1 2 3 4 5 6 7 8 9 10

I (amperes 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14

V (volts) 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70

Slope from graph V vs. I = 5 𝑅𝐸𝑋𝑃'𝑇 = 5 johms

𝑅𝑇𝐻𝐸𝑂 = 5 i ohms
%error = 0 i%
 III. VARIATION OF CURRENT WITH RESISTANCE, VOLTAGE CONSTANT

Constant Voltage, V = 1 volts

TRIAL 1 2 3 4 5 6 7 8 9 10

R (ohms) 20 21 22 23 24 25 26 27 28 29

1/R (mhos 0.05 0.048 0.045 0.043 0.042 0.04 0.038 0.037 0.036 0.034

I (amperes) 0.05 0.048 0.045 0.044 0.042 0.04 0.039 0.037 0.036 0.035

Slope from graph I vs. 1/R = 0.98 𝑉𝐸𝑋𝑃'𝑇 = 0.98 jvolts

𝑉𝑇𝐻𝐸𝑂 = 1 i volts
%error = 2 i%
 IV. RESISTIVITY AND RESISTANCE

−6
Metal = Nichrome 𝜌𝑆𝑇𝐴𝑁𝐷𝐴𝑅𝐷 = 1.50 x 10 𝛀m
−8 2
Diameter = 0.0003 m Cross-sectional area =7.07 x 10 𝑚
−6
Slope from graph = 20 𝛀/m 𝜌𝐸𝑋𝑃'𝑇 = 1.41 x 10 𝛀m
%error = 6 i%

TRIAL 1 2 3 4 5 6 7 8 9 10

Length, L (m) 0.1 0.20 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.00

𝑅𝑀𝐸𝐴𝑆𝑈𝑅𝐸𝐷 (ohm) 2 4.2 6 7.5 9.5 11.3 14 16 18 20

 GUIDE QUESTIONS

1. In Part I of the experiment, what happened to the voltage across the resistance box as the
current through it was increased? What is the relationship between voltage and current when
resistance is fixed?
- The voltage across the resistance box increased as the current increased,
demonstrating the direct relationship between voltage and current when resistance is
fixed according to Ohm's Law (V=I⋅R).

2. In Part II, what happened to the voltage as resistance is decreased What is the relationship
between voltage and resistance when current is maintained constant?
- There is an inverse relationship between voltage and resistance when the current is held
constant (V=I⋅R).

3. In Part III, what happened to current when resistance is increased? What is the relationship
between current and resistance when voltage is constant?
- During Part III, increasing resistance decreased current, showcasing the inverse
𝑉
relationship between current and resistance when voltage is constant. 𝐼 = 𝑅

4. From the plot of 𝑅𝑀𝐸𝐴𝑆𝑈𝑅𝐸𝐷 vs. 𝐿, what is the relationship between the length of the wire
and its resistance? How do you solve for the resistivity of the wire from the slope of this plot?
- The plot of resistance against the length of the wire displayed a linear relationship,
𝐿
where the slope provides the resistivity of the wire through the formula 𝑅 = 𝜌 𝐴
​, with A
being the cross-sectional area.

5. Two wires, A and B, are made of the same material, have the same diameter, and are at the
same temperature. Wire A is twice as long as wire B, and the same voltage is applied across
the ends of each wire. If the current through wire A is 𝐼, what is the current through wire B?
- Since wire A is twice as long as wire B and both experience the same voltage, the
resistance of wire A is twice that of wire B due to the direct proportionality between
𝐿
length and resistance 𝑅 = 𝜌 𝐴
​. If the current through wire A is I, the current through
2𝑉
wire B (𝐼𝐵) is 𝑅𝐴
, where RA​is the resistance of wire A.