Scribd Logo
Upload

Welcome to Scribd!

  • 3 views

    Lecture Notes (Dragged)

    Uploaded by

    yawas50511
    The document discusses translations of graphs, which involve moving a graph vertically or horizontally without changing its shape or size. Specifically, it describes: 1) Vertical translation, which moves the graph parallel to the y-axis by adding or subtracting a value d from the original function. 2) This effectively shifts all y-coordinates up or down by d units, as represented by the equations y = f(x) + d or y = f(x) - d. 3) An example demonstrates translating the parabola y = x^2 up by adding 1 to the function, and down by subtracting 1 from the function.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd
    Flag for inappropriate content

    You might also like

    Lecture Notes (Dragged)

    Uploaded by

    yawas50511
    3 views1 page
    The document discusses translations of graphs, which involve moving a graph vertically or horizontally without changing its shape or size. Specifically, it describes: 1) Vertical translation, which moves the graph parallel to the y-axis by adding or subtracting a value d from the original function. 2) This effectively shifts all y-coordinates up or down by d units, as represented by the equations y = f(x) + d or y = f(x) - d. 3) An example demonstrates translating the parabola y = x^2 up by adding 1 to the function, and down by subtracting 1 from the function.

    Original Description:

    Copyright

    © © All Rights Reserved

    Available Formats

    PDF, TXT or read online from Scribd

    Did you find this document useful?

    Is this content inappropriate?

    Report this Document
    The document discusses translations of graphs, which involve moving a graph vertically or horizontally without changing its shape or size. Specifically, it describes: 1) Vertical translation, which moves the graph parallel to the y-axis by adding or subtracting a value d from the original function. 2) This effectively shifts all y-coordinates up or down by d units, as represented by the equations y = f(x) + d or y = f(x) - d. 3) An example demonstrates translating the parabola y = x^2 up by adding 1 to the function, and down by subtracting 1 from the function.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd
    Flag for inappropriate content
    Download as pdf or txt
    3 views1 page

    Lecture Notes (Dragged)

    Uploaded by

    yawas50511
    The document discusses translations of graphs, which involve moving a graph vertically or horizontally without changing its shape or size. Specifically, it describes: 1) Vertical translation, which moves the graph parallel to the y-axis by adding or subtracting a value d from the original function. 2) This effectively shifts all y-coordinates up or down by d units, as represented by the equations y = f(x) + d or y = f(x) - d. 3) An example demonstrates translating the parabola y = x^2 up by adding 1 to the function, and down by subtracting 1 from the function.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd
    Flag for inappropriate content
    Download as pdf or txt
    of 1

    2020 SAJC JC1 H2 Mathematics

    Lecture Notes
    6.1 Transformations of Graph: Translation, Scaling, Combination of transformations

    (A) Translation
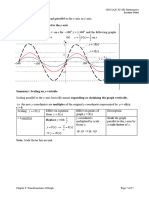
    A translation is a movement of the graph vertically (parallel to y-axis)
    or horizontally (parallel to x-axis) without changing its shape or size.

    Example 1: Vertical Translation parallel to the y-axis

    Consider the following graphs, where d is a positive number:


    (i) y = f(x) = x 2
    (ii) y = f(x) + d = x 2  d
    (iii) y = f(x) – d = x 2  d .
    y
    y = f(x) + d

    y = f(x)

    y = f(x) – d
    d
    x
    0

    –d

    Summary : Translation on y-variable

    Translation in the y – direction means moving the graph up or down parallel to the y-axis.

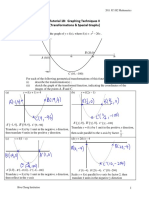
    Translation: Effect on equation from Effect on points of Description


    y  f ( x)  d y  f ( x) graph y = f(x)
    For any positive or Replace y with y  d y-coordinates changed Translate graph by d
    negative d y  f ( x)  y  d  f ( x) by d units units in the positive y-
    E.g., y  f ( x )  1 (p, q)  (p, q + d) direction.
     y  f ( x)  d
    y  f ( x )  ( 1) Translate graph by |d|
    units in the negative y-
    direction.

    Chapter 6: Transformations of Graph Page 2 of 37

    You might also like