Area bisectors[edit]

Main article: Bisection § Area bisectors and perimeter bisectors

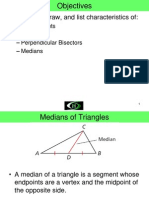
There are an infinitude of lines that bisect the area of a triangle. Three of them are
the medians of the triangle (which connect the sides' midpoints with the opposite
vertices), and these are concurrent at the triangle's centroid; indeed, they are the only
area bisectors that go through the centroid. Any line through a triangle that splits both the
triangle's area and its perimeter in half goes through the triangle's incenter (the center of
its incircle). There are either one, two, or three of these for any given triangle.

Any line through the midpoint of a parallelogram bisects the area.

All area bisectors of a circle or other ellipse go through the center, and
any chords through the center bisect the area. In the case of a circle they are the
diameters of the circle.

Optimization[edit]
Given a wire contour, the surface of least area spanning ("filling") it is a minimal surface.
Familiar examples include soap bubbles.

The question of the filling area of the Riemannian circle remains open.[30]

The circle has the largest area of any two-dimensional object having the same perimeter.

A cyclic polygon (one inscribed in a circle) has the largest area of any polygon with a
given number of sides of the same lengths.

A version of the isoperimetric inequality for triangles states that the triangle of greatest
area among all those with a given perimeter is equilateral.[31]

The triangle of largest area of all those inscribed in a given circle is equilateral; and the
triangle of smallest area of all those circumscribed around a given circle is equilateral. [32]

The ratio of the area of the incircle to the area of an equilateral triangle, , is larger than
that of any non-equilateral triangle.[