EVEN AND ODD FUNCTIONS

There are different types of functions in mathematics that

we study. We can determine whether a function is even or
odd algebraically or graphically. Even and Odd functions
can be checked by plugging in the negative inputs (-x) in
place of x into the function f(x) and considering the
corresponding output value. Even and odd functions are
classified on the basis of their symmetry relations. Even and
odd functions are named based on the fact that the power
function f(x) = xn is an even function, if n is even, and f(x) is
an odd function if n is odd.

Let us explore other even and odd functions and

understand their properties, graphs, and the use of even
and odd functions in integration. A function can be even or
odd or both even and odd, or neither even nor odd. Let's
explore various examples to understand the concept.

What are Even and Odd Functions?

Generally, we consider a real-valued function to be even or

odd. To identify if a function is even or odd, we plug in -x in
place of x into the function f(x), that is, we check the output
value of f(-x) to determine the type of the function. Even and
odd functions are symmetrical. Let us first understand their
definitions.

Even and Odd Functions Definition

Even Function - For a real-valued function f(x), when the

output value of f(-x) is the same as f(x), for all values of x in
the domain of f, the function is said to be an even function.
An even function should hold the following equation: f(-x)
= f(x), for all values of x in D(f), where D(f) denotes the
domain of the function f. In other words, we can say that the
equation f(-x) - f(x) = 0 holds for an even function, for all x.
Let us consider an example, f(x) = x2.

f(-x) = (-x)2 = x2 for all values of x, as the square of a negative

number is the same as the square of the positive value of
the number. This implies f(-x) = f(x), for all x. Hence, f(x) =
x2 is an even function. Similarly, functions like x4, x6, x8, etc.
are even functions.

Odd Function - For a real-valued function f(x), when the

output value of f(-x) is the same as the negative of f(x), for
all values of x in the domain of f, the function is said to be
an odd function. An odd function should hold the following
equation: f(-x) = -f(x), for all values of x in D(f), where D(f)
denotes the domain of the function f. In other words, we can
say that the equation f(-x) + f(x) = 0 holds for an odd
function, for all x

Let us consider an example, f(x) = x3.

f(-x) = (-x)3 = -(x3) for all values of x, as the cube of a

negative number is the same as the negative of the cube of
the positive value of the number. This implies f(-x) = -f(x),
for all x. Hence, f(x) = x3 is an odd function. Similarly,
functions like x5, x7, x9 etc. are odd functions.

Both Even and Odd Functions - A real-valued function f(x)

is said to be both even and odd if it satisifies f(-x) = f(x) and
f(-x) = -f(x) for all values of x in the domain of the
function f(x). There is only one function which is both even
and odd and that is the zero function, f(x) = 0 for all x. We
know that for zero function, f(-x) = -f(x) = f(x) = 0, for all
values of x. Hence, f(x) = 0 is an even and odd function.

Neither Even Nor Odd Function - A real-valued

function f(x) is said to be neither even nor odd if it does not
satisfy f(-x) = f(x) and f(-x) = -f(x) for atleast one value of x
in the domain of the function f(x). Let us consider an
example to understand the definition better. Consider f(x) =
2x5 + 3x2 + 1, f(-x) = 2(-x)5 + 3(-x)2 + 1 = -2x5 + 3x2 + 1
which is neither equal to f(x) nor -f(x). Hence, f(x) = 2x5 +
3x2 + 1 is neither even nor odd function.

Even and Odd Functions in Trigonometry

In this section, we will segregate trigonometric functions as

even and odd functions. We have six trigonometric ratios
(sine, cosine, tangent, cotangent, cosecant, and secant).
These trigonometric ratios give positive values in different
quadrants for various measures of angles.

In the first quadrant (where x and y coordinates are all

positive), all six trigonometric ratios have positive values.
In the second quadrant, only sine and cosecant are positive.
In the third quadrant, only tangent and cotangent are
positive. In the fourth quadrant, only cosine and secant are
positive. Based on these signs, we will categorize them as
even and odd functions.

If a trigonometric ratio is even or odd can be checked

through a unit circle. An angle measured in anticlockwise
direction is a positive angle whereas the angle measured in
the clockwise direction is a negative angle.
• sinθ = y, sin(-θ) = -y; Therefore, sin(-θ) = -sinθ.
Hence, sinθ is an odd function.
• cosθ = y, cos(-θ) = y; Therefore, cos(-θ) = cosθ.
Hence, cosθ is an even function.
• tanθ = y, tan(-θ) = -y; Therefore, tan(-θ) = -tanθ.
Hence, tanθ is an odd function.
• cosecθ = y, cosec(-θ) = -y; Therefore, cosec(-θ) = -
cosecθ. Hence, cosecθ is an odd function.
• secθ = y, sec(-θ) = y; Therefore, sec(-θ) = secθ.
Hence, secθ is an even function.
• cotθ = y, cot(-θ) = -y; Therefore, cot(-θ) = -cotθ.
Hence, cotθ is an odd function.
Integral Properties of Even and
Odd Functions
The integral of a function gives the area below the curve. We
use properties of even and odd functions while solving
definite integrals. For that, we need to know the limits of the
integral and the nature of the function. If the function is
even or odd, and the interval is [-a, a], we can apply the
following two rules:

𝑎 𝑎
When f(x) is even, ∫−𝑎 𝑓(𝑥)𝑑𝑥 = 2 ∫0 𝑓(𝑥)𝑑𝑥

𝑎
When f(x) is odd, ∫−𝑎 𝑓(𝑥)𝑑𝑥 = 0

Even and Odd Functions Graph

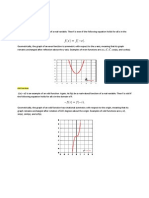
Let us now see how even and odd functions behave

graphically. The graph of an even function is symmetric
with respect to the y-axis. In other words, the graph of an
even function remains the same after reflection about the y-
axis. For any two opposite input values of x, the function
value will remain the same all along the curve.

Whereas the graph of an odd function is symmetric with

respect to the origin. In other words, the graph of an odd
function is at the same distance from the origin but in
opposite directions. For any two opposite input values of x,
the function has opposite y values. Here are a few examples
of even and odd functions.

Figure 1. Even Function Graph

 Figure 2. Odd Function Graph

Properties of Even and Odd Functions

• The sum of two even functions is even and the sum

of two odd functions is odd.
• The difference between two even functions is even
and the difference between two odd functions is
odd.
• The sum of an even and odd function is neither even
nor odd unless one of them is a zero function.
• The product of two even functions is even and the
product of two odd functions is also an even
function.
 • The product of an even and an odd function is odd.
• The quotient of two even functions is even and the
quotient of two odd functions is also an even
function.
• The quotient of an even and an odd function is odd.
• The composition of two even functions is even and
the composition of two odd functions is odd.
• The composition of an even and an odd function is
even.

Important Notes on Even and Odd Functions

• A function f(x) is even if f(-x) = f(x), for all values of
x in D(f) and it is odd if f(-x) = -f(x), for all values of
x.
• In trigonometry, cos(θ) and sec(θ) are even
functions, and sin(θ), cosec(θ), tan(θ), cot(θ) are
odd functions.
• The graph even function is symmetric with respect
to the y-axis and the graph of an odd function is
symmetric about the origin.
• f(x) = 0 is the only function that is an even and odd
function.