Professional Documents
Culture Documents
Coord Geo Revision
Coord Geo Revision
Uploaded by
adhrit1mitraCopyright:
Available Formats
You might also like
- Acoustics of Porous Media PDFDocument356 pagesAcoustics of Porous Media PDFGhassen LaouiniNo ratings yet
- P3 JAN 21 Revision Worksheet All ChaptersDocument3 pagesP3 JAN 21 Revision Worksheet All ChaptersSheikh HassanNo ratings yet
- MARK: . NAME: . Total: 40 TEACHER: . . TIME: 50 Mins DATE: ..Document2 pagesMARK: . NAME: . Total: 40 TEACHER: . . TIME: 50 Mins DATE: ..Frances ThorpeNo ratings yet
- Maths BDocument3 pagesMaths Bnithyakrishna518No ratings yet
- Challenging Questions v2 QDocument20 pagesChallenging Questions v2 QAdwin JY LowNo ratings yet
- s4 ch3 Quadratic Equations Ex1 EngDocument4 pagess4 ch3 Quadratic Equations Ex1 EngDon LiaoNo ratings yet
- W4 CH 1-4 Mixed QuestionsDocument6 pagesW4 CH 1-4 Mixed QuestionsJessicaNo ratings yet
- Worksheet Class 9Document4 pagesWorksheet Class 9elashwarapu.ishithaNo ratings yet
- Class IX Mathematics CH-3 and 4 AsignmentDocument3 pagesClass IX Mathematics CH-3 and 4 AsignmentPriyankAhujaNo ratings yet
- Pure Mathematics Revision Worksheet Month 8Document4 pagesPure Mathematics Revision Worksheet Month 8Le Jeu LifeNo ratings yet
- Hyper-PDF For Math!!!!!Document71 pagesHyper-PDF For Math!!!!!Yasmeen KassabNo ratings yet
- Multiple Choice QuestionsDocument6 pagesMultiple Choice QuestionsHANo ratings yet
- IntegrationDocument3 pagesIntegrationSontosh BhattacharjeeNo ratings yet
- Al 21 p2 RevisionDocument6 pagesAl 21 p2 RevisionSenuja ChammithaNo ratings yet
- Midyear Sc2024Document2 pagesMidyear Sc2024ahmad younesNo ratings yet
- Midterm-Math 211fall 2023Document7 pagesMidterm-Math 211fall 2023aalrjl08No ratings yet
- Pure Mathematic Revision Worksheet Month 3Document2 pagesPure Mathematic Revision Worksheet Month 3Le Jeu LifeNo ratings yet
- FC 11216 - Analytic Geometry and Linear AlgebraDocument3 pagesFC 11216 - Analytic Geometry and Linear AlgebraAbi ebayNo ratings yet
- VIII-Algebra-Revision WorksheetDocument5 pagesVIII-Algebra-Revision Worksheetanousha1488No ratings yet
- Mathematics For Natural Sciences Math 1011 Worksheet On Chapters 3 and 4Document2 pagesMathematics For Natural Sciences Math 1011 Worksheet On Chapters 3 and 4Eyob LakewNo ratings yet
- Screenshot 2023-11-08 at 08.35.27Document5 pagesScreenshot 2023-11-08 at 08.35.27alicejessicapreesNo ratings yet
- 11MME SAT 1 Practice Test PDFDocument7 pages11MME SAT 1 Practice Test PDFJewel SANTHOSHNo ratings yet
- 2.2 Consolidation QuestionsDocument6 pages2.2 Consolidation QuestionsmildasaadiNo ratings yet
- North Sydney Boys 2017 Year 10 Maths Yearly & SolutionsDocument18 pagesNorth Sydney Boys 2017 Year 10 Maths Yearly & SolutionsIbrahim ElyasehNo ratings yet
- Instructions:: Has A Maximum Point at (2, )Document8 pagesInstructions:: Has A Maximum Point at (2, )WAH XIN YEE MoeNo ratings yet
- AASL Calculus 1 Review PDFDocument10 pagesAASL Calculus 1 Review PDFJosh Student - MeiiselNo ratings yet
- Pure Mathematics Revision Worksheet Month 7Document3 pagesPure Mathematics Revision Worksheet Month 7Le Jeu LifeNo ratings yet
- Seeta High School Post - 2023 S.6 Pure Mathematics Paper 1Document3 pagesSeeta High School Post - 2023 S.6 Pure Mathematics Paper 1vanessablessed99950% (2)
- p4 May Batch (Upto CH 4)Document2 pagesp4 May Batch (Upto CH 4)Bibi Marium SiddiqueNo ratings yet
- P4 MAY BATCH (Upto CH 4)Document2 pagesP4 MAY BATCH (Upto CH 4)Bibi Marium SiddiqueNo ratings yet
- SCI101SC - PHA101SC - (B) - Assessment - 202101 - Joy and FisherDocument6 pagesSCI101SC - PHA101SC - (B) - Assessment - 202101 - Joy and FisherAhmed Sami YounisNo ratings yet
- Third Space Learning Quadratic Simultaneous Equations GCSE Worksheet 1Document9 pagesThird Space Learning Quadratic Simultaneous Equations GCSE Worksheet 1Sabrin AhmedNo ratings yet
- Chapter 10 Test PDFDocument7 pagesChapter 10 Test PDFDarrenPurtillWrightNo ratings yet
- MathsDocument2 pagesMathsPLAYER100No ratings yet
- 3 - 5 Sketching Circles and TransformationsDocument6 pages3 - 5 Sketching Circles and Transformationsyi lingNo ratings yet
- REVIEW QUESTIONS CH Wowo QuadraticDocument2 pagesREVIEW QUESTIONS CH Wowo Quadraticwfffs7bcr4No ratings yet
- Differential Calculus Practice TestDocument8 pagesDifferential Calculus Practice Testchirantha150No ratings yet
- MTH P1recess Work AlevelDocument11 pagesMTH P1recess Work AlevelEfrataNo ratings yet
- Third Space Learning Quadratic Graphs GCSE WorksheetDocument15 pagesThird Space Learning Quadratic Graphs GCSE WorksheetZoonieFRNo ratings yet
- Mid Yr Pure p1 (Set 2)Document5 pagesMid Yr Pure p1 (Set 2)anesu taperaNo ratings yet
- Answer All Questions (In Black Ink) For 50 MarksDocument2 pagesAnswer All Questions (In Black Ink) For 50 MarksNchenti RazakNo ratings yet
- Pure Mathematics Revision Worksheet Month 5Document4 pagesPure Mathematics Revision Worksheet Month 5Le Jeu LifeNo ratings yet
- M5 Extended - EoY Exam 2021Document14 pagesM5 Extended - EoY Exam 2021Edu De LuqueNo ratings yet
- Sec 2 Math 2Document2 pagesSec 2 Math 2Garly UraniNo ratings yet
- s.5 Mid-Term 2 PureDocument3 pagess.5 Mid-Term 2 PurekelvinhunghanaNo ratings yet
- 9 - Standard Linear Relations - SAT - 2023Document6 pages9 - Standard Linear Relations - SAT - 2023Lino VariNo ratings yet
- S 5 Holidayworkapril 2021Document2 pagesS 5 Holidayworkapril 2021PentNo ratings yet
- CG-1 (Basic) : Xis EducationDocument5 pagesCG-1 (Basic) : Xis EducationAbrar ChowdhuryNo ratings yet
- Review Limit and DifferentialDocument2 pagesReview Limit and Differentialadrian kwokNo ratings yet
- MCR3U Practice ExamDocument4 pagesMCR3U Practice ExamGaganpreet KaurNo ratings yet
- Topical Guidance of SPM MathematicsDocument39 pagesTopical Guidance of SPM MathematicsSEOW INN LEENo ratings yet
- Wa0045.Document3 pagesWa0045.Bonglav JemasonNo ratings yet
- Target-40 Maths XiiDocument9 pagesTarget-40 Maths XiiRohith SNo ratings yet
- Webinar 1 - Student's Copy-1Document5 pagesWebinar 1 - Student's Copy-1amalin natasha zainal fitriNo ratings yet
- Revision Form 5 UD 1 2024Document6 pagesRevision Form 5 UD 1 2024Crystal Hui HuiNo ratings yet
- IGCSE - FPM - Chapter 1 - Graphs - Assignment 4Document1 pageIGCSE - FPM - Chapter 1 - Graphs - Assignment 4binuk wNo ratings yet
- Maths - PB A 2 - CLASS - XII 22-23 FinalDocument5 pagesMaths - PB A 2 - CLASS - XII 22-23 FinalsidharthNo ratings yet
- Test 7 SMKCH Ques&AnsDocument8 pagesTest 7 SMKCH Ques&AnsLIM YEE WEN MoeNo ratings yet
- Straight LineDocument10 pagesStraight Linerohan.sengupta2007No ratings yet
- ACHIEVE 1 SolutionsDocument2 pagesACHIEVE 1 SolutionsLeviNo ratings yet
- CBSE Class 10 Mathematics HOTs TrigonometryDocument17 pagesCBSE Class 10 Mathematics HOTs TrigonometryAbhayNo ratings yet
- On Interpretability of Artificial Neural Networks A SurveyDocument20 pagesOn Interpretability of Artificial Neural Networks A SurveyERICK MANUEL RUBIONo ratings yet
- QMT337Document11 pagesQMT337pwince88No ratings yet
- 10.3.2 Infinite Square Well: −Iωt −Iet/¯ HDocument4 pages10.3.2 Infinite Square Well: −Iωt −Iet/¯ HChandler LovelandNo ratings yet
- Aime Solutions: Mortemetinteritum BoleDocument6 pagesAime Solutions: Mortemetinteritum BoleAbhishek JainNo ratings yet
- All About Bearing and Lubrication A Complete GuideDocument20 pagesAll About Bearing and Lubrication A Complete GuideJitu JenaNo ratings yet
- Managing Economies of Scale in The Supply Chain: Cycle InventoryDocument33 pagesManaging Economies of Scale in The Supply Chain: Cycle InventoryMahmud KhanNo ratings yet
- Roots: Bracketing Methods: Berlin ChenDocument19 pagesRoots: Bracketing Methods: Berlin ChenlapuNo ratings yet
- Sta 301 FormulasDocument10 pagesSta 301 Formulasqyh570% (2)
- Btech Eee Autonomous SyllabusDocument148 pagesBtech Eee Autonomous Syllabusnalluri_08No ratings yet
- EMF QB For Mid-1Document1 pageEMF QB For Mid-1madhueeNo ratings yet
- Size Reduction: Department of Chemical Engineering University of Engineering & Technology PeshawarDocument60 pagesSize Reduction: Department of Chemical Engineering University of Engineering & Technology PeshawarRavid GhaniNo ratings yet
- Goa Board Class VII Mathematics Sample Paper - 1 Time: 3 Hours Total Marks: 90Document7 pagesGoa Board Class VII Mathematics Sample Paper - 1 Time: 3 Hours Total Marks: 90Divya bholaNo ratings yet
- Column Supported Embankments - AsceDocument24 pagesColumn Supported Embankments - AsceAnonymous D5s00DdUNo ratings yet
- Validation of Analytical MethodsDocument41 pagesValidation of Analytical MethodsHani HazaraniNo ratings yet
- Feynman ParadoxDocument3 pagesFeynman ParadoxBabai KunduNo ratings yet
- Solving Quadratic Equations by The Quadratic Formula: Objectives 1Document11 pagesSolving Quadratic Equations by The Quadratic Formula: Objectives 1Joy CloradoNo ratings yet
- Fundamentals of Transformer ProtectionDocument37 pagesFundamentals of Transformer ProtectionVikas Oza100% (1)
- 2.3 Table of DataDocument5 pages2.3 Table of DataDuc Duy NguyenNo ratings yet
- Machine Learning-Lecture 02Document28 pagesMachine Learning-Lecture 02Amna AroojNo ratings yet
- UT Dallas Syllabus For Math1325.501.11f Taught by Paul Stanford (phs031000)Document2 pagesUT Dallas Syllabus For Math1325.501.11f Taught by Paul Stanford (phs031000)UT Dallas Provost's Technology GroupNo ratings yet
- Electronics 12 04302 v2Document13 pagesElectronics 12 04302 v2Eswariah VannamNo ratings yet
- Statistics - Review 26 Oct 2022Document31 pagesStatistics - Review 26 Oct 2022Tsz Wun CHOWNo ratings yet
- Blaise PascalDocument8 pagesBlaise PascalArinta Pramudya HeryantiNo ratings yet
- Lecture C Ring Signature PDFDocument13 pagesLecture C Ring Signature PDFpipiNo ratings yet
- FULL Download Ebook PDF Intermediate Algebra Algebra Within Reach 6th Edition PDF EbookDocument51 pagesFULL Download Ebook PDF Intermediate Algebra Algebra Within Reach 6th Edition PDF Ebooklinda.rabon566100% (44)
- Prolog Lists AdvancedDocument22 pagesProlog Lists AdvancedCristina LarisaNo ratings yet
- Socially Priming Dogs in An Overimitation TaskDocument11 pagesSocially Priming Dogs in An Overimitation TaskConstanza LucoNo ratings yet
- Parallel Lines ChallengingDocument3 pagesParallel Lines ChallengingKelly CornellNo ratings yet
Coord Geo Revision
Coord Geo Revision
Uploaded by
adhrit1mitraOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Coord Geo Revision
Coord Geo Revision
Uploaded by
adhrit1mitraCopyright:
Available Formats
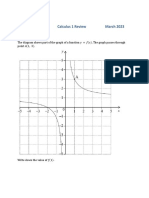
Coordinate Geometry Review
1. Show that (1,3) lies on 3𝑥𝑥 − 2𝑦𝑦 = 3 7. Consider the point 𝐴𝐴(2,3). The line 𝐶𝐶𝐶𝐶𝐶𝐶
2. Show that 𝐴𝐴(1,4), 𝐵𝐵(−2, −4) and 𝐶𝐶(7,20) passes through 𝐴𝐴 and has y-intercept at
are collinear. 𝐶𝐶 and x-intercept at 𝑇𝑇. Find the equation
3. Consider the points 𝐴𝐴(1, −3), 𝐵𝐵(3,2), 𝐶𝐶(2,4) of the line 𝐶𝐶𝐶𝐶𝐶𝐶 such that the ratio of the
and 𝐷𝐷(0, −1). area of ∆𝐶𝐶𝐶𝐶𝐶𝐶 to the area of ∆𝑇𝑇𝑇𝑇𝑇𝑇 is 2: 3.
a) Show that the diagonals of 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 8. Draw an example of a circle that has 3
bisect each other. points of intersections with a parabola,
b) What type of quadrilateral can showing all 3 points of intersection.
you conclude 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 is? 9. Find the angle between the line 2𝑥𝑥 − 3𝑦𝑦 −
4. Consider the points 𝐴𝐴(2,1) and 𝐵𝐵(5,2). 6 = 0 and the positive x axis.
a) Find the point 𝐶𝐶 such that 𝐵𝐵 is the 10. How many points of intersection
midpoint of 𝐴𝐴𝐴𝐴. do graphs of the following have:
b) Find the point 𝐷𝐷 such that 𝐷𝐷 𝑦𝑦 = 2𝑥𝑥 + 3
a) � 2
bisects 𝐴𝐴𝐴𝐴 externally in the ratio 5𝑥𝑥 + 5𝑦𝑦 2 = 9
𝑦𝑦 = 2 − 𝑥𝑥 2
2:3 b) � 2
𝑥𝑥 + (𝑦𝑦 − 1)2 = 2
c) How are 𝐴𝐴, 𝐶𝐶 and 𝐷𝐷 related to each
11. Find all points of intersection of
other geometrically?
the graphs of 𝑦𝑦 = 𝑥𝑥 3 and 𝑦𝑦 = 𝑥𝑥
5. Consider the lines 𝑥𝑥 − 2𝑦𝑦 = 5
𝑥𝑥 12. Draw a neat sketch of the region
and 𝑦𝑦 = + 2 𝑦𝑦 < 2𝑥𝑥 − 1
2
a) Explain why the lines are parallel. defined by: �4𝑥𝑥 − 16𝑦𝑦 − 16 ≤ 0
b) Find the distance between the 𝑥𝑥 < 2
lines 13. Find the area of the region in 12.
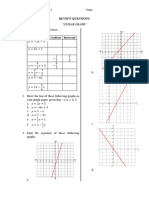
6. Draw a neat sketch of:
a) 𝑦𝑦 = 2(𝑥𝑥 − 1)2 − 2
b) 𝑥𝑥 2 + 𝑦𝑦 2 + 1 = 2𝑥𝑥 − 𝑦𝑦
You might also like
- Acoustics of Porous Media PDFDocument356 pagesAcoustics of Porous Media PDFGhassen LaouiniNo ratings yet
- P3 JAN 21 Revision Worksheet All ChaptersDocument3 pagesP3 JAN 21 Revision Worksheet All ChaptersSheikh HassanNo ratings yet
- MARK: . NAME: . Total: 40 TEACHER: . . TIME: 50 Mins DATE: ..Document2 pagesMARK: . NAME: . Total: 40 TEACHER: . . TIME: 50 Mins DATE: ..Frances ThorpeNo ratings yet
- Maths BDocument3 pagesMaths Bnithyakrishna518No ratings yet
- Challenging Questions v2 QDocument20 pagesChallenging Questions v2 QAdwin JY LowNo ratings yet
- s4 ch3 Quadratic Equations Ex1 EngDocument4 pagess4 ch3 Quadratic Equations Ex1 EngDon LiaoNo ratings yet
- W4 CH 1-4 Mixed QuestionsDocument6 pagesW4 CH 1-4 Mixed QuestionsJessicaNo ratings yet
- Worksheet Class 9Document4 pagesWorksheet Class 9elashwarapu.ishithaNo ratings yet
- Class IX Mathematics CH-3 and 4 AsignmentDocument3 pagesClass IX Mathematics CH-3 and 4 AsignmentPriyankAhujaNo ratings yet
- Pure Mathematics Revision Worksheet Month 8Document4 pagesPure Mathematics Revision Worksheet Month 8Le Jeu LifeNo ratings yet
- Hyper-PDF For Math!!!!!Document71 pagesHyper-PDF For Math!!!!!Yasmeen KassabNo ratings yet
- Multiple Choice QuestionsDocument6 pagesMultiple Choice QuestionsHANo ratings yet
- IntegrationDocument3 pagesIntegrationSontosh BhattacharjeeNo ratings yet
- Al 21 p2 RevisionDocument6 pagesAl 21 p2 RevisionSenuja ChammithaNo ratings yet
- Midyear Sc2024Document2 pagesMidyear Sc2024ahmad younesNo ratings yet
- Midterm-Math 211fall 2023Document7 pagesMidterm-Math 211fall 2023aalrjl08No ratings yet
- Pure Mathematic Revision Worksheet Month 3Document2 pagesPure Mathematic Revision Worksheet Month 3Le Jeu LifeNo ratings yet
- FC 11216 - Analytic Geometry and Linear AlgebraDocument3 pagesFC 11216 - Analytic Geometry and Linear AlgebraAbi ebayNo ratings yet
- VIII-Algebra-Revision WorksheetDocument5 pagesVIII-Algebra-Revision Worksheetanousha1488No ratings yet
- Mathematics For Natural Sciences Math 1011 Worksheet On Chapters 3 and 4Document2 pagesMathematics For Natural Sciences Math 1011 Worksheet On Chapters 3 and 4Eyob LakewNo ratings yet
- Screenshot 2023-11-08 at 08.35.27Document5 pagesScreenshot 2023-11-08 at 08.35.27alicejessicapreesNo ratings yet
- 11MME SAT 1 Practice Test PDFDocument7 pages11MME SAT 1 Practice Test PDFJewel SANTHOSHNo ratings yet
- 2.2 Consolidation QuestionsDocument6 pages2.2 Consolidation QuestionsmildasaadiNo ratings yet
- North Sydney Boys 2017 Year 10 Maths Yearly & SolutionsDocument18 pagesNorth Sydney Boys 2017 Year 10 Maths Yearly & SolutionsIbrahim ElyasehNo ratings yet
- Instructions:: Has A Maximum Point at (2, )Document8 pagesInstructions:: Has A Maximum Point at (2, )WAH XIN YEE MoeNo ratings yet
- AASL Calculus 1 Review PDFDocument10 pagesAASL Calculus 1 Review PDFJosh Student - MeiiselNo ratings yet
- Pure Mathematics Revision Worksheet Month 7Document3 pagesPure Mathematics Revision Worksheet Month 7Le Jeu LifeNo ratings yet
- Seeta High School Post - 2023 S.6 Pure Mathematics Paper 1Document3 pagesSeeta High School Post - 2023 S.6 Pure Mathematics Paper 1vanessablessed99950% (2)
- p4 May Batch (Upto CH 4)Document2 pagesp4 May Batch (Upto CH 4)Bibi Marium SiddiqueNo ratings yet
- P4 MAY BATCH (Upto CH 4)Document2 pagesP4 MAY BATCH (Upto CH 4)Bibi Marium SiddiqueNo ratings yet
- SCI101SC - PHA101SC - (B) - Assessment - 202101 - Joy and FisherDocument6 pagesSCI101SC - PHA101SC - (B) - Assessment - 202101 - Joy and FisherAhmed Sami YounisNo ratings yet
- Third Space Learning Quadratic Simultaneous Equations GCSE Worksheet 1Document9 pagesThird Space Learning Quadratic Simultaneous Equations GCSE Worksheet 1Sabrin AhmedNo ratings yet
- Chapter 10 Test PDFDocument7 pagesChapter 10 Test PDFDarrenPurtillWrightNo ratings yet
- MathsDocument2 pagesMathsPLAYER100No ratings yet
- 3 - 5 Sketching Circles and TransformationsDocument6 pages3 - 5 Sketching Circles and Transformationsyi lingNo ratings yet
- REVIEW QUESTIONS CH Wowo QuadraticDocument2 pagesREVIEW QUESTIONS CH Wowo Quadraticwfffs7bcr4No ratings yet
- Differential Calculus Practice TestDocument8 pagesDifferential Calculus Practice Testchirantha150No ratings yet
- MTH P1recess Work AlevelDocument11 pagesMTH P1recess Work AlevelEfrataNo ratings yet
- Third Space Learning Quadratic Graphs GCSE WorksheetDocument15 pagesThird Space Learning Quadratic Graphs GCSE WorksheetZoonieFRNo ratings yet
- Mid Yr Pure p1 (Set 2)Document5 pagesMid Yr Pure p1 (Set 2)anesu taperaNo ratings yet
- Answer All Questions (In Black Ink) For 50 MarksDocument2 pagesAnswer All Questions (In Black Ink) For 50 MarksNchenti RazakNo ratings yet
- Pure Mathematics Revision Worksheet Month 5Document4 pagesPure Mathematics Revision Worksheet Month 5Le Jeu LifeNo ratings yet
- M5 Extended - EoY Exam 2021Document14 pagesM5 Extended - EoY Exam 2021Edu De LuqueNo ratings yet
- Sec 2 Math 2Document2 pagesSec 2 Math 2Garly UraniNo ratings yet
- s.5 Mid-Term 2 PureDocument3 pagess.5 Mid-Term 2 PurekelvinhunghanaNo ratings yet
- 9 - Standard Linear Relations - SAT - 2023Document6 pages9 - Standard Linear Relations - SAT - 2023Lino VariNo ratings yet
- S 5 Holidayworkapril 2021Document2 pagesS 5 Holidayworkapril 2021PentNo ratings yet
- CG-1 (Basic) : Xis EducationDocument5 pagesCG-1 (Basic) : Xis EducationAbrar ChowdhuryNo ratings yet
- Review Limit and DifferentialDocument2 pagesReview Limit and Differentialadrian kwokNo ratings yet
- MCR3U Practice ExamDocument4 pagesMCR3U Practice ExamGaganpreet KaurNo ratings yet
- Topical Guidance of SPM MathematicsDocument39 pagesTopical Guidance of SPM MathematicsSEOW INN LEENo ratings yet
- Wa0045.Document3 pagesWa0045.Bonglav JemasonNo ratings yet
- Target-40 Maths XiiDocument9 pagesTarget-40 Maths XiiRohith SNo ratings yet
- Webinar 1 - Student's Copy-1Document5 pagesWebinar 1 - Student's Copy-1amalin natasha zainal fitriNo ratings yet
- Revision Form 5 UD 1 2024Document6 pagesRevision Form 5 UD 1 2024Crystal Hui HuiNo ratings yet
- IGCSE - FPM - Chapter 1 - Graphs - Assignment 4Document1 pageIGCSE - FPM - Chapter 1 - Graphs - Assignment 4binuk wNo ratings yet
- Maths - PB A 2 - CLASS - XII 22-23 FinalDocument5 pagesMaths - PB A 2 - CLASS - XII 22-23 FinalsidharthNo ratings yet
- Test 7 SMKCH Ques&AnsDocument8 pagesTest 7 SMKCH Ques&AnsLIM YEE WEN MoeNo ratings yet
- Straight LineDocument10 pagesStraight Linerohan.sengupta2007No ratings yet
- ACHIEVE 1 SolutionsDocument2 pagesACHIEVE 1 SolutionsLeviNo ratings yet
- CBSE Class 10 Mathematics HOTs TrigonometryDocument17 pagesCBSE Class 10 Mathematics HOTs TrigonometryAbhayNo ratings yet
- On Interpretability of Artificial Neural Networks A SurveyDocument20 pagesOn Interpretability of Artificial Neural Networks A SurveyERICK MANUEL RUBIONo ratings yet
- QMT337Document11 pagesQMT337pwince88No ratings yet
- 10.3.2 Infinite Square Well: −Iωt −Iet/¯ HDocument4 pages10.3.2 Infinite Square Well: −Iωt −Iet/¯ HChandler LovelandNo ratings yet
- Aime Solutions: Mortemetinteritum BoleDocument6 pagesAime Solutions: Mortemetinteritum BoleAbhishek JainNo ratings yet
- All About Bearing and Lubrication A Complete GuideDocument20 pagesAll About Bearing and Lubrication A Complete GuideJitu JenaNo ratings yet
- Managing Economies of Scale in The Supply Chain: Cycle InventoryDocument33 pagesManaging Economies of Scale in The Supply Chain: Cycle InventoryMahmud KhanNo ratings yet
- Roots: Bracketing Methods: Berlin ChenDocument19 pagesRoots: Bracketing Methods: Berlin ChenlapuNo ratings yet
- Sta 301 FormulasDocument10 pagesSta 301 Formulasqyh570% (2)
- Btech Eee Autonomous SyllabusDocument148 pagesBtech Eee Autonomous Syllabusnalluri_08No ratings yet
- EMF QB For Mid-1Document1 pageEMF QB For Mid-1madhueeNo ratings yet
- Size Reduction: Department of Chemical Engineering University of Engineering & Technology PeshawarDocument60 pagesSize Reduction: Department of Chemical Engineering University of Engineering & Technology PeshawarRavid GhaniNo ratings yet
- Goa Board Class VII Mathematics Sample Paper - 1 Time: 3 Hours Total Marks: 90Document7 pagesGoa Board Class VII Mathematics Sample Paper - 1 Time: 3 Hours Total Marks: 90Divya bholaNo ratings yet
- Column Supported Embankments - AsceDocument24 pagesColumn Supported Embankments - AsceAnonymous D5s00DdUNo ratings yet
- Validation of Analytical MethodsDocument41 pagesValidation of Analytical MethodsHani HazaraniNo ratings yet
- Feynman ParadoxDocument3 pagesFeynman ParadoxBabai KunduNo ratings yet
- Solving Quadratic Equations by The Quadratic Formula: Objectives 1Document11 pagesSolving Quadratic Equations by The Quadratic Formula: Objectives 1Joy CloradoNo ratings yet
- Fundamentals of Transformer ProtectionDocument37 pagesFundamentals of Transformer ProtectionVikas Oza100% (1)
- 2.3 Table of DataDocument5 pages2.3 Table of DataDuc Duy NguyenNo ratings yet
- Machine Learning-Lecture 02Document28 pagesMachine Learning-Lecture 02Amna AroojNo ratings yet
- UT Dallas Syllabus For Math1325.501.11f Taught by Paul Stanford (phs031000)Document2 pagesUT Dallas Syllabus For Math1325.501.11f Taught by Paul Stanford (phs031000)UT Dallas Provost's Technology GroupNo ratings yet
- Electronics 12 04302 v2Document13 pagesElectronics 12 04302 v2Eswariah VannamNo ratings yet
- Statistics - Review 26 Oct 2022Document31 pagesStatistics - Review 26 Oct 2022Tsz Wun CHOWNo ratings yet
- Blaise PascalDocument8 pagesBlaise PascalArinta Pramudya HeryantiNo ratings yet
- Lecture C Ring Signature PDFDocument13 pagesLecture C Ring Signature PDFpipiNo ratings yet
- FULL Download Ebook PDF Intermediate Algebra Algebra Within Reach 6th Edition PDF EbookDocument51 pagesFULL Download Ebook PDF Intermediate Algebra Algebra Within Reach 6th Edition PDF Ebooklinda.rabon566100% (44)
- Prolog Lists AdvancedDocument22 pagesProlog Lists AdvancedCristina LarisaNo ratings yet
- Socially Priming Dogs in An Overimitation TaskDocument11 pagesSocially Priming Dogs in An Overimitation TaskConstanza LucoNo ratings yet
- Parallel Lines ChallengingDocument3 pagesParallel Lines ChallengingKelly CornellNo ratings yet