C1 January 2006 (Edexcel) ©ExamSolutions.co.

uk

Edexcel GCE
Mathematics
C1 January 2006

Model Solutions

www.examsolutions.co.uk

WARNING

You are not allowed to use

a calculator in this paper.

Please Note
The solutions provided here are not necessarily the only way to solve the problems.

For more practice papers visit www.examsolutions.co.uk Page 1

C1 January 2006 (Edexcel) ©ExamSolutions.co.uk

No Model Solutions – C1 January 2006 (Edexcel)

1
(
x3 − 4 x 2 + 3x ≡ x x 2 − 4 x + 3 ) Pull out x as a common factor
and then factorise the quadratic
≡ x ( x − 3)( x − 1) expression

2 Substitute n = 1 into un +1 = ( u n − 3 ) .
u2 = (1 − 3)
2
2
a)
u1+1 = ( u1 − 3 )
2

= ( −2 )
2 So

∴ u 2 = (1 − 3 )
2

=4

Substitute n = 2 into un +1 = ( u n − 3 ) .
2

u3 = ( 4 − 3)
2
u 2 +1 = ( u 2 − 3 )
2
So

= (1) u3 = ( 4 − 3 )
2
∴
2

=1
Substitute n = 3 into un +1 = ( u n − 3 ) .
2

u 3 +1 = ( u 3 − 3 )
2
So
u4 = (1 − 3)
2
∴ u 4 = (1 − 3 )
2

= ( −2 )
2

=4

Every even term u2 , u4 , u6

b) u20 = 4 etc gives 4.

For more practice papers visit www.examsolutions.co.uk Page 2

C1 January 2006 (Edexcel) ©ExamSolutions.co.uk

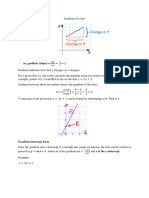
3 a) When x = 3,

Substitute x = 3 into y = 5 − 2 x
y = 5 − 2 ( 3)
to check that y = −1 .
= −1

∴ P ( 3, −1) lies on L

Any line having the form y = mx + c has

gradient m.
b) Gradient of L = −2 In this case the gradient m = −2.

∴ Gradient of line perpendicular to L = 1

2
The perpendicular gradient to
a line with gradient m is − 1
m

A quick rule is to invert the

fraction and change the sign.

∴ Equation of perpendicular line through P is:

The equation of a line with gradient m,
y − ( −1) = 1
2 ( x − 3) passing through a point ( x1 , y1 ) is given

∴ 2y + 2 = x −3 by: y − y1 = m ( x − x1 )
∴ x − 2y − 5 = 0 In this case m = 2 , ( x1 , y1 ) = ( 3, − 1)
1

Multiply both sides by 2.

Rearrange into the required
form ax + by + c = 0

For more practice papers visit www.examsolutions.co.uk Page 3

C1 January 2006 (Edexcel) ©ExamSolutions.co.uk

4 a) 6 6
y = 2x2 −
n
We need to rewrite 3
in the form ax in
x3 x
preparation for differentiating. To do this,
= 2 x 2 − 6 x −3 use the law for indices
1 −n 6 1 −3
n
≡x So 3
= 6× 3
= 6x
x x x

dy −4
∴ = 4 x + 18 x −4 Simplify 18x by using the law for indices
dx 1 1 18
−n −4
18 x ≡ So 18 x = 18 × =
= 4x + 4
n 4 4
x x x
x

b)
Do not forget to insert brackets
since there is more than one term 6 n
and remember to write dx. We need to rewrite 3
in the form ax in
x
preparation for integrating. To do this,
⎛ 6⎞ use the law for indices
∫ y dx = ∫ ⎜⎝ 2 x −
2
⎟ dx
x3 ⎠ 1 −n 6 1 −3
≡x So = 6× = 6x
(
= ∫ 2x − 6x ) dx
n 3 3
2 −3 x x x

2 x 3 6 x −2 To integrate each of the terms, add 1

= − +c to each terms power of x and then
3 −2 divide by the new power
2 x3
+ 3x −2 + c
n +1
= ax
∫ ax dx =
n
3 i.e.
n +1
2 x3 3
= + 2 +c
3 x Note: Do not forget the constant c.

−2
Simplify 3x by using the law for indices
−n 1 −2 1 3
x ≡ n
So 3 x = 3 × 2
= 2
x x x

For more practice papers visit www.examsolutions.co.uk Page 4

C1 January 2006 (Edexcel) ©ExamSolutions.co.uk

5 To simplify 45 look for any factors that are

a) 45 = 9 × 5
square numbers of 45. In this case 9 is the
= 9× 5 only number which meets this requirement.
Since 9 × 5 = 45 then 45 = 9×5
=3 5
Then use the multiplication rule for surds
i.e. ab ≡ a× b

b)
We need to remove the 3 − 5 in the
denominator this is called rationalising.
a
To rationalise anything of the form
b− c
multiply top and bottom by b + c
In this case b = 3 and c = 5 .

( ) = 2 (3 + 5 ) × (3 + 5 )
2 3+ 5 This is the expanded form of

(3 − 5 ) (3 − 5 ) (3 + 5 ) ( 3 + 5 )( 3 + 5 )
2 ( 9 + 3 5 + 3 5 + 5)
Note: Remember 5× 5 =5
=
9+3 5 −3 5 −5
( )
This is the expanded form of

=
2 14 + 6 5
( 3 − 5 )( 3 + 5 )
4
Note: Remember 5× 5 =5
28 + 12 5
=
4
Now divide each term on the top
= 7+3 5 by 4.

For more practice papers visit www.examsolutions.co.uk Page 5

C1 January 2006 (Edexcel) ©ExamSolutions.co.uk

6 a) Since f ( x + a ) represents a translation of a units to the left parallel to the x-axis.

By comparing f ( x + a ) to f ( x + 1) , where a = 1 the graph of y = f ( x ) is
translated 1 unit to the left.

x
(0, 0) (3, 0)

b) Since a f ( x ) represents a stretch parallel to the y-axis of scale factor a.

By comparing a f ( x ) with 2 f ( x ) , where a = 2 the graph of y = f ( x ) is
stretched by a factor of 2 parallel to the y-axis.

y
(0, 3) moves up by a factor
of 2 to give (0, 6)
(0, 6)

x
(1, 0) (4, 0)

These points do not move

For more practice papers visit www.examsolutions.co.uk Page 6

C1 January 2006 (Edexcel) ©ExamSolutions.co.uk

c) Since f( x ) represents a stretch parallel to the x-axis of scale factor a.

1
a

By comparing f ( x ) with f ( x ) , where a = 2 the graph of y = f ( x ) is stretched

1
a
1
2

by a factor of 2 parallel to the x-axis.

y
This point does not move

(0, 3)

x
(2, 0) (8, 0)

7 11 birthday allowance = £500

th

12 birthday allowance = 500 + 200 = £700

th

a) Total allowance immediately after her 12th birthday = 500 + 700

= £1200

b) Amount of allowance on her 18th birthday = 500 + ( 8 − 1)( 200 )

= 500 + 7 × 200
= £1900
The allowances form an arithmetic progression going up in steps of
£200. We can use the nth term of an arithmetic progression here.

Use the formula for the nth term of an arithmetic progression.

n term = a + ( n − 1) d . Where the first term = a and the common
th

difference = d. In this case, a = 500, d = 200 and n = 8

11 year = 1 term
th st
Note:
12 year = 2
th nd
term

18 year = 8 term
th th

For more practice papers visit www.examsolutions.co.uk Page 7

C1 January 2006 (Edexcel) ©ExamSolutions.co.uk

c) The allowances form an Arithmetic Progression with 1st term a = 500,

common difference d = 200 and number of terms is n = 8.
n
The sum S n of an A.P. is given by S n = [ 2a + ( n − 1) d ]
2

Total allowances up to her 18th birthday = 82 ⎡⎣ 2 ( 500 ) + ( 8 − 1)( 200 ) ⎤⎦

= 4 [1000 + 1400]
= 4 ( 2400 )
= £9600

The sum S n of an A.P. is given by

d) Sn = 32000
n
∴ n2 ⎡⎣ 2 ( 500 ) + ( n − 1)( 200 ) ⎤⎦ = 32000 Sn =[ 2a + ( n − 1) d ]
2
∴ n
2 (1000 + 200n − 200 ) = 32000 where the 1st term a = 500, common
difference d = 200 and the number of
∴ n2 ( 800 + 200n ) = 32000 terms n is to be found.
∴ 400n + 100n 2 = 32000
Divide both sides by 100
∴ 4n + n 2 = 320
∴ n 2 + 4n − 320 = 0 Next factorise the quadratic.
∴ ( n + 20 )( n − 16 ) = 0
∴ n + 20 = 0 or n − 16 = 0
∴ n = −20 or n = 16
n = −20 is not practical as n > 0
So n = 16 as n > 0

∴ Alice's age = 11 + 15 Note: The 16th term represents an

= 26 years interval of 15 years.

For more practice papers visit www.examsolutions.co.uk Page 8

C1 January 2006 (Edexcel) ©ExamSolutions.co.uk

8 f ' ( x ) is the result of differentiating f ( x ) .

So reversing the process f ( x ) must be the
result of integrating f ' ( x ) .

5x2 + 2
f '( x) = 3 + 1
x2
Next split the fraction into two fractions by
1

dividing each term in the numerator by x . 2

5x + 2 2
∴ f ( x) = ∫ 3 + 1 dx
x2
⎛ 5x2 2 ⎞
= ∫ ⎜ 3 + 1 + 1 ⎟ dx 1. Subtract powers when dividing x by x .
2 1
2

⎝ x x2⎠
2

(
= ∫ 3 + 5x 2 + 2 x−
3 1
2
) dx 2. We need to rewrite
2
1
into the form ax
n

x 2

To integrate each of the terms, in preparation for integrating. To do this, we

add 1 to each terms power of x use the law for indices
and then divide by the new power
1 −n 2 1 − 12
ax
n +1 ≡x So 1 = 2× 1 = 2x
∫ ax
n
dx = x
n 2 2
i.e. x x
n +1

5 1
5x 2
2x 2

= 3x + + +c Note: Do not forget the constant c.

5 1
2 2

= 3x + 2 x + 4 x 2 + c [1]
5 1
2 Simplify each term.

When x = 1, y = 6 Since (1, 6) lies on the curve y = f ( x ) then

it must satisfy the equation. Use this fact to
find the constant c.
Sub into [1]
6 = 3 (1) + 2 (1) 2 + 4 (1) 2 + c
5 1

∴ 6 = 3+ 2+ 4+ c
(1) ( 1)
m m

∴ 6 = 9+c
n
= n
= 1 for all values of m and n.

∴ c = −3

Sub c = −3 into [1]

∴ f ( x ) = 3x + 2 x 2 + 4 x 2 − 3
5 1

For more practice papers visit www.examsolutions.co.uk Page 9

C1 January 2006 (Edexcel) ©ExamSolutions.co.uk

9 When the curve C, y = ( x − 1) x − 4 ( 2

)
crosses the x-axis, y = 0.

a) x-coordinate of P = −2 So (
0 = ( x − 1) x − 4
2
)
x-coordinate of Q = 2
∴ x −1 = 0 x −4=0
2
or
∴ x =1 x =4
2
or

x = 1 is clearly not the required point.

x =4
2
So

∴ x=± 4
∴ x = ±2

b)
(
y = ( x − 1) x 2 − 4 ) Expand the brackets

= x3 − 4 x − x 2 + 4 To differentiate each of the terms, multiply

each term by its power of x and then
subtract 1 from its power.
dy
∴ = 3x 2 − 4 − 2 x i.e. If y = ax then
n dy
= anx
n −1

dx dx
dy
∴ = 3x 2 − 2 x − 4 Note: The differential of kx is k, and the
dx differential of a constant k is 0.

Rearrange to give the required form.

c) When x = −1

Find the gradient of the tangent

dy
= 3 ( −1) − 2 ( −1) − 4
2
dy
dx by substituting x = −1 into
dx
= 3+ 2− 4
=1 Gradient of tangent is 1

∴ Equation of tangent at ( −1, 6 ) is:

y − 6 = 1( x − −1) The equation of a line with gradient m,
passing through a point ( x1 , y1 ) is
∴ y − 6 = x +1
given by: y − y1 = m ( x − x1 )
∴ y = x+7
In this case m = 1, ( x1 , y1 ) = ( −1, 6 )
Rearrange to give the
required result.

For more practice papers visit www.examsolutions.co.uk Page 10

C1 January 2006 (Edexcel) ©ExamSolutions.co.uk

Gradients at R must be the same as the

dy
d) When =1 tangent y = 1x + 7 so set
dy
to 1
dx dx
∴ 3x 2 − 2 x − 4 = 1
∴ 3x 2 − 2 x − 5 = 0 dy
= 3x − 2 x − 4
2
Remember
∴ ( 3 x − 5 )( x + 1) = 0 dx

∴ 3x − 5 = 0 or x + 1 = 0
∴ x= 5
3 or x = −1

So x = 5
3 at R as x = −1 was the other point.

When x = 5
3

y = ( 53 − 1) ⎡( 53 ) − 4 ⎤
⎣
2

⎦
Substitute x = 5
3 (
into y = ( x − 1) x − 4
2
)
= ( 23 )( 259 − 4 ) 25
−4= 25
− 36

=( )( − )
9 9 9
2 11
3 9

= − 27
22
The exact answer was required
so leave as a fraction.

∴ R ( 53 , − 27
22
)

10 a) To complete the square: carry out the

following steps:
1) Look at the x term, i.e. 2x and halve
the 2 to give 1.
x 2 + 2 x + 3 ≡ ( x + 1) − 1 + 3
2
(Note: This is often referred to as
halving the coefficient of x.)
2) Now write down ( x + 1)
2

3) Now ( x + 1) when expanded gives

2

x 2 + 2 x + 1 which is nearly identical to

x + 2x + 3
2

4) The 1 is not required so subtract it

5) And add in the required 3

≡ ( x + 1) + 2
2

≡ ( x + a) + b
2

Where a = 1 and b = 2

For more practice papers visit www.examsolutions.co.uk Page 11

C1 January 2006 (Edexcel) ©ExamSolutions.co.uk

b)

Transformations of the function f ( x ) = x 2

1) Think of the graph of 2) Replacing x with x + 1 3) Adding 2 to a function

f ( x ) = x2 causes the graph of the causes the graph of the
function f ( x ) = x to
2 function to move up 2
units.
move 1 unit to the left.
y y y
f ( x) = x 2

3
x x x
-1 -1
f ( x + 1) = ( x + 1)
2

f ( x + 1) + 2 = ( x + 1) + 2
2

When x = 0,
(0, 3) y = ( 0) + 2 ( 0) + 3
2

(-1, 2) ∴ y=3

x
-1

Discriminant = ( 2 ) − 4 (1)( 3) For any quadratic ax + bx + c = 0 the

2 2
c)
discriminant is b − 4ac
2

= 4 − 12
So for the quadratic x + 2 x + 3 = 0
2

= −8 where a = 1, b = 2 and c = 3 the

discriminant equals 2 − 4 (1)( 3 )
2

Since the discriminant is negative, there will be no real roots for

x 2 + 2 x + 3 = 0.
∴ The graph will not cross the x-axis.

For more practice papers visit www.examsolutions.co.uk Page 12

C1 January 2006 (Edexcel) ©ExamSolutions.co.uk

For any quadratic ax + bx + c = 0 ,

2

d) x 2 + kx + 3 = 0 the roots (solutions) are given by:

−b ± b − 4ac
2

x=
2a
For no real roots 'b 2 − 4ac < 0 '
There will be no roots if the discriminant
∴ k 2 − 4 (1)( 3) < 0 b − 4ac is negative since one cannot
2

square root a negative value.

∴ k 2 − 12 < 0
∴ Critical values are k = ± 12 Critical values are where
k − 12 = 0
2

∴ k = 12
2

∴ k = ± 12

Draw a sketch of y = k − 12 and label the critical values on the k-axis. Look for
2

the values of k that give y values less than zero.

In other words this will be the values of k where the corresponding y values are
below the k-axis.

y
y = k 2 − 12

k
− 12 12

y < 0 here i.e. k − 12 < 0

2

From the graph

Leave the answer in surd form
− 12 < k < 12
as requested but simplify 12
−2 3 < k < 2 3
12 = 4×3 = 4× 3 =2 3

For more practice papers visit www.examsolutions.co.uk Page 13