SH1657

Continuity

I. Continuity on a Point
Definition 1.1
A function is continuous at ! = " if the following conditions are satisfied:
i. (") is defined
ii. lim (!) exists
$→&
iii. lim (!) = (").
$→&
Otherwise, is said to be discontinuous at ! = ".
Example 1.1
Test if (!) = ! ' + 2! + 1 is continuous at ! = 0.
Solution:
To test continuity, we must check if the three (3) conditions stated in Definition 1.1.
i. (0) = (0)' + 2(0) + 1 = 1
Since 1 is a real number, (!) is defined at ! = 0.
ii. lim (!) = (0)' + 2(0) + 1 = 1
$→*
Since 1 is a real number, lim (!) exists.
$→*
iii. (0) = 1 = lim (!)
$→*
Since all three (3) conditions of continuity are satisfied, (!) = ! ' + 2! + 1 is indeed
continuous at ! = 0.

Polynomials, like the previous example, are continuous everywhere. Define

,(!) = -/ ! / + -/34 ! /34 + ⋯ + -' ! ' + -4 ! + -* where -/ , -/34 , … , -' , -4 , -* ∈ ℝ
Let " ∈ ℝ,
,(") = -/ " / + -/34 " /34 + ⋯ + -' " ' + -4 " + -* ∈ ℝ
Hence, ,(!) is defined at ! = ".
lim ,(!) = lim(-/ ! / + -/34 ! /34 + ⋯ + -' ! ' + -4 ! + -* )
$→& $→&
= lim(-/ ! / ) + lim(-/34 ! /34 ) + ⋯ + lim(-' ! ' ) + lim(-4 !) + lim(-* )
$→& $→& $→& $→& $→&
= -/ lim ! / + -/34 lim(! /34 ) + ⋯ + -' lim(! ' ) + -4 lim(!) + -*
$→& $→& $→& $→&
= -/ " / + -/34 " /34 + ⋯ + -' " ' + -4 " + -* ∈ ℝ
Hence, lim ,(!) exists.
$→&
,(") = -/ " / + -/34 " /34 + ⋯ + -' " ' + -4 " + -* = lim ,(!)
$→&
Hence, ,(") = lim ,(!)
$→&
Therefore, ,(!) is continuous at any real number ".

Theorem 1.1
Suppose that and 9 are continuous at ! = ", then the following are true:
i. ( ± 9) is continuous at ! = ",
ii. ( ∙ 9) is continuous at ! = " and
<
iii. ;>? is continuous at ! = ", if 9(") ≠ 0.

04 Handout 1 *Property of STI

Page 1 of 5
 SH1657

Proof of (i):
If and 9 are continuous at ! = ", then
lim[ (!) ± 9(!)] = lim (!) ± lim 9(!)
$→& $→& $→&
= (") ± 9(")
= ( ± 9)(")
∎
Theorem 1.2
Suppose that lim 9(!) = B and is continuous at B. Then
$→&
lim C9(!)D = ;lim 9(!)? = (B)
$→& $→&

Proof:
To prove the result, we will use the definition of limits. That is, given any E > 0, there
is a number G > 0 for which whenever 0 < |! − "| < G, then J C9(!)D − (B)J < E.
Since is continuous at B, we know that lim (M) = (B). Consequently, by
K→L
definition, given any E > 0, there is a G4 > 0 for which
| (M) − (B)| < E, whenever |M − B| < G4 .
Furthermore, since lim 9(!) = B, we can make 9(!) as close to B as desired by
$→&
making ! sufficiently close to ". In particular, there must be a G' > 0 for which |9(!) −
B| < G4 whenever 0 < |! − "| < G' . It now follows that if 0 < |! − "| < G' , then
|9(!) − B| < G4 , so that
J C9(!)D − (B)J < E.
∎
Corollary 1.1
Suppose that 9 is continuous at " and is continuous at 9("). Then the composition ∘9
is continuous at ".
Proof:
From Theorem 1.2, we have
lim( ∘ 9)(!) = lim C9(!)D
$→& $→&
= ;lim 9(!)?
$→&
= C9(")D
= ( ∘ 9)(")
∎
The previous theorems and corollary can be used to simplify the testing of continuity.

Example 1.2
tan ! is continuous at ! = 0.
Proof:
Let (!) = sin ! and 9(!) = cos !. Since and 9 are continuous at ! = 0 and 9(0) =
<($)
cos(0) = 1 ≠ 0, then by Theorem 1.1 (iii), >($) = tan ! is continuous at ! = 0.
∎

04 Handout 1 *Property of STI

Page 2 of 5
 SH1657

Example 1.3
sin' ! − cos ' ! is continuous at ! = 0
Proof:
Let (!) = ! ' , 9(!) = sin !, and ℎ(!) = cos !. Since 9 and ℎ are continuous at ! = 0
and , which is a polynomial, is continuous at 9(0) = 0 and ℎ(0) = 1, then by Corollary
1.1, ( ∘ 9)(!) = sin' ! and ( ∘ ℎ)(!) = cos ' ! are continuous at ! = 0. Let P = ∘ 9
and Q = ∘ ℎ. Since P and Q are continuous at ! = 0, by Theorem 1.1 (i), (P + Q)(!) =
C( ∘ 9) + ( ∘ ℎ)D(!) = ( ∘ 9)(!) + ( ∘ ℎ)(!) = sin' ! + cos' ! is continuous at
! = 0.
∎
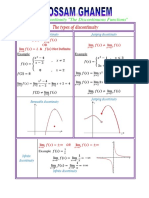
II. Discontinuity on a Point
To understand continuity, it helps to see how a function can fail to be continuous. All of
the important functions used in calculus and analysis are continuous except at isolated points.
Such points are called points of discontinuity. If " is a point of discontinuity, at least one (1)
of the three (3) statements in Definition 1.1 must fail to be true. There are several types of
discontinuity.

Definition 2.1
A function has a hole or a removable discontinuity at " if lim (!) exists and either of
$→&
the conditions are true:
i. (") exists but lim (!) ≠ ("), OR
$→&
ii. (") does not exist.
The discontinuity can be removed by changing the definition of (or giving definition to, if
undefined) (!) at " so that (") = lim (!).
$→&

Example 2.1
The following functions has a hole or removable discontinuity at the specified points:
$ R 34
(!) = at ! = 1
$34
i.
! + 2! − 1
' ! < −1
ii. 9(!) = S −3 U ! = −1 at ! = −1
−! − 2! − 3
' ! > −1
Proof:
i.
!' − 1
lim (!) = lim
$→4 $→4 ! − 1
(! − 1)(! + 1)
= lim
$→4 !−1
= lim (! + 1)
$→4
=2
$ R 34
Therefore, lim
$→4 $34
exists.
1' − 1 0
(1) = = = UVWXMXYZUV\MX
1−1 0

04 Handout 1 *Property of STI

Page 3 of 5
 SH1657

Therefore, (1) does not exist. Hence, satisfies Definition 2.1 (ii). This implies that
has a removable discontinuity at ! = 1.
ii.
lim 9(!) = lim^(−! ' − 2! − 3) = −(−1)' − 2(−1) − 3 = −2
$→34^ $→34
lim _ 9(!) = lim_(! ' + 2! − 1) = (−1)' + 2(−1) − 1 = −2
$→34 $→34
Therefore, lim 9(!) = −2
$→34
9(−1) = −3, hence 9(−1) exists. But,
9(−1) = 3 ≠ −2 = lim 9(!)
$→34
9 satisfies Definition 2.1 (i). Therefore, 9 has a removable discontinuity at ! = −1.
∎
Definition 2.2
A function has a jump discontinuity at " if lim^ (!) and lim_ (!) exist, but
$→& $→&
lim^ (!) ≠ lim_ (!). The size of the jump is the absolute value of the difference of the
$→& $→&
one-sided limits, that is ` lim^ (!) − lim_ (!)`. Moreover, (") may or may not exist.
$→& $→&

Though jump discontinuities are not common in functions given by simple formulas, they
occur frequently in engineering — for example, the square waves in electrical engineering, or
the sudden discharge of a capacitor.

Definition 2.3
An essential discontinuity is the case where at least one (1) of the one-sided limits does
not exist or is infinite. A special case is an infinite/asymptotic discontinuity where (")
may or may not exist, and at least one (1) of the one-sided limits diverges to ± infinity.

III. Continuity on an Interval

Definition 3.1
We say that
i. is continuous on (\, b) if is continuous at every point on an open interval (\, b).
ii. Ug continuous on [\, b) if (\) exists and it is continuous on (\, b). Moreover, it
must be continuous on the right at \, that is
lim^ (!) = (\).
$→j
iii. is continuous on (\, b] if (b) exists and it is continuous on (\, b). Moreover, it
must be continuous on the left at b, that is
lim_ (!) = (b).
$→k
iv. is continuous on [\, b] if it is continuous on (\, b] and [\, b).

References:
Discontinuities. (n.d.). Retrieved from http://faculty.bucks.edu/taylors/calculus/discon.html on June
15, 2016
Continuity and Discontinuity. (n.d.). Retrieved from
http://math.mit.edu/~jspeck/18.01_Fall%202014/Supplementary%20notes/01c.pdf on June
15, 2016

04 Handout 1 *Property of STI

Page 4 of 5
 SH1657

Minton, R. & Smith, R. (2016). Basic Calculus. McGraw Hill Education.

Coburn, J. (2016). Pre-Calculus. McGraw Hill Education.

04 Handout 1 *Property of STI

Page 5 of 5