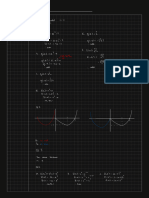
A set SEIR" is an OPEN SET eff : IRE IR then the PARTIAL DERIVATIVE LetKEIN If .

eff : IRE IR then the PARTIAL DERIVATIVE LetKEIN If . f :RV-IR and all its partial
y) f(x, y)
lim
is (y)
+t, -

iff ExES J Bp(x)[S of f w r . . t .

x =
t -0
derivatives up to order k are continuous
,
.
t

+) y).
f(x,
my
+
INTERIOR POINT while that wr.t. is )=
say that f function of class C"
A point xEIR" is an we is a

Br (x) [S Let f : R-I have all its partial derivatives at If this is true forkEI then fis SMOOTH
of Siff J . .

EIR" then the GRADIENT of fata is

point x@R" is BOUNDARYPOINT a
A
Let f :R> IR be smooth
a
-

(a) , ...
.

iff rel Br(x) has points #S 4 f(a) = (a)

of f
the TAYLOR APPROMATION
.
,

A set S & IR" is a CLOSED SET iff Let UEIR" , llull = .

1 , the DIRECTIONAL DERIV
about at IR" is
it contains all its boundary points off at direction is Duf(a)= tu-f(a)
noHf(a)n + E(h)
.

f(x) f(a) + + f(a) on +

=

A set S is CONVERSET iff Ex, YES, Tm

: nEIR", 11411 1 f:REIREDy(a) = =
Af(a)ou
a ,
Y diff where E(h) tends to zero faster than 1h1 ?
Let UEIR" be open = f : U Ris DIFFERENTIABLE
the line segment sy ? S +

-o
.

A set S is a BOUNDED SET iff at a + U if f(ath) f(a) + Df(a)oh + E(h) where

=

= Br(x) such that S[Br(s) · E(h)/n + 0 as + 0 .

Sinc = -
- +...
3
COS = - ..

6
A PARAMETRISATION of a curve C Th Let HER be open Iff has continuous partial
- E
.

1 +x = 1+ ...

diff'ble e= 1+x + ...

is a continuous fan r: It IR" derivatives on U the f on U I

= 1 +x+ x2
- ..
---

log (1 + x) = x

where IfR and C = Er(t) tEl3 :

.
UEIR f ,
: U-1R , fas continuous partial deriva-

The LEVEL CURVE of f : IRC-IR tives U The TANGENT PLANE at EU is

on .

The HESSIAN MATRIX of a Smooth

at CERR is Lc :
EXER" f(x) c3 : =
.
2 = f(a) + z((a)](x -
Pi) f: R-IR , f(a) = f(x y 2) , ,
is

The GRAPH of f IR"> IR is the UER" open f : U-IR is DIFFERENTIABLE

I
:

I
-

,
fxZ

firs
fay
M SERV
set : f(x , ..., = 3 at a EU then f is CONTINUOUS at a
Hf( y z)
= =
n+ , ,

IR"-IRM F(a) (f (a) fin(a))

T fyy fyz
A function f : IR-IR" is CONTINUOUS Let F :
,
=
, , ..., then
fzx fzy fzz
iff all its the JACOBIAN matrix of Fat is
components are continuous .
a

11
# sequence (n) in IR" converses A Quadratic Form Q() = nQh

=
to aeiff
lim k Pl -
= 0 .

Positive definite
n > 00
-
·
iff Q (h) > 0th Fo
Let AIRL be open then f : A- IR
: ·
Negative definite iff Q(h) < 0th0
is CONTINUOUS at oEIR iff · Positive semidefinite iff Q(h) 0th ,

- sequence (xn) A: ·
Negative semidefinite iff QCh10th
xn + xo = f(xn) + f(x0) If f : IR"-IR AND ITS PARTIAL DERIV ARE CONT ·
In definite iff Q(h) takes both +, -

Thm : If f : IR-IR is continuous at a EIR" then fis DIFFERENTIABLE at a

diff at atIRY, f : RM-IR" diff

*
then so areF(x , y) = f(x), G(x, y) = f(y) G :R-IR at
.
Let Q(H) = <x+ 2Dxy + Ey2
IR"-IR CHAINRULE G(a) EIRY, H : FOG then It is
y)Q( , [i]
Thm : If f , g : are continuous :
,
= x ,
=
·

atso then so are f+g , f-g, fg .

diff at a and JH(a) JF (G(a) Ja (a)= .

If g(x) #O ,
then so is f/g . SPECIAL CASES :
·
det Q >0
,0 = POS DEF .
.

Thm : If f : IR"-IR g : /R = IR are contin 1. G : IR-IR", F :R"-IR , H = FOG then

, · detQ) 0
,
CO = NEGDEF .

nuous then so is gof : IR"- IR

. H'(t) Jy(t) = =
TF(G(t))(t) · det Qc0 = Indefinite .

Let r: I- IR" I = (a , b) <R

, to El . 11 G : IR"-IR , F :REIR, H = FoG
.
then
,

the DERIVATIVE of rat to is ↑ H(a) = F'(G(a)) TG(a) SYLVESTER'S THM : LetMeMn(R)

o th) r(to)
(to) =
-

be symmetric and M (m , 1)
,
THE GRADIENT IS 1 TO LEVEL CURVES
=

h . ,

(mm) My= Ms S(
Thm Let +: I - 1R", r(t) = (r(t) , rn(t) Let f : IR"-IR be smooth , I , be its level curve
.,
Mr= M
. .

M
.
=
....,
·

where ri : IR R are differentiable parametrised by r(t) then Ar(t) ELc :

then =
( ...,) Xf(r(t)) o (t) = 0 ·
If det MkJOKE POS DEF

Mao
· If det
/R-IR" then THE GRADIENT ISL TOLEVEL SURFACES
Let r: the velocity of V .
= NEG . DEF .

t-iR det M2k-1 O

at t is v(t) = and speed is (v(t)). Let f : be smooth and eS given

Df(x) + S ALGORITHM : Given a function , convert

Letter v
= The displacement by f(x , y , z) = 0 then .

Taylor's then check QCh)

,
to ,
·

of a particle over the interval .

e F(x , 4 , z) = f(x , y) -
z
g
.
EIR" if J By(a)7 ExcfBy(a) f(x) < f(a)
[t , t 2] is given by => x = =
(b+/xx 85(y 1) ,
-
MAXIMUM at a
, .

St (Sist)dt)
,
MINIMUM at a EIR" if J By(a)-ExEBylal f(x), fla) .

=> XFLf pl off

,

~ (tz) r(t , ) -
= =
.
NF1 to tan . . .

MIN/MAD drop" "

,
STRICT LOCAL : =

The length of a curve V Gr(t) = :

te [a , b)
Let f : IR"> IR be diffble with local extremum at a

(b , (t))d
-

is given by then its partial derivatives vanishata: Mf(a) =

o
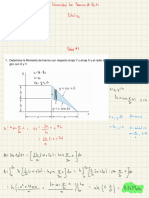
 BOLZANO-WEIERSTRASS Every bounded LAGRANGE MULTIPLIERS General version : Let D & IR2 between
IR" f: IR" IR smooth and let s be
sequence in has convergent subsequence of $ 02 [a bJ-IR
Let > be
a
-

the graphs : , so that

,

If f : -> IR is continuous closed and bounded given by S= ExEIR" : g(x) 03 =

where
\(,y)EI
· on

is smooth too D = : (a b) , p, D12y = P23

g : /RV-IR
,
that
>
- then it attains its max and min values one .
.
Suppose
& g(x) O and that Fattains its (we can also switch the places of sand y
If f is smooth and has critical point a and Q(h)
·

is the quadratic form f's 2D Taylor Polynom maximum minimum value Sato
of .
or on in the other case)
f(a+ h) = f(a) + ]Q(h) then JxER7XF(x(0) X Xg(x0) =
·
Then :

Staleya se
Then def - a is minimum
corollary (Multiple Constraints)
I
2
.
Q pos a :

= a is
Q neg def a maximum
·

· Q indef = a is a saddle point .

DF(() =

[xiXgi(o)
LEAST SQUARES METHOD DIMENSION REDUCTION ALGORITHM

Let (i , yi) points and f :R"-IR

be data 1. Write in the
following form : IF DISCONTINUOUS THEN
depends on " then the least
parameters[C;] F(u) = [((xi , yi) (4 , · 42))2 = uoSu NO TANGENT PLANE !

/S S ]
squares estimate off are the values of di
21
where s
. f(x, y)
for cyto
=
=
e
= g ,
(f(:) Yi)?
.

that minimise F(d , ...., [n) -

·
for 0
xy
=

[xi)S
·

Let &R"be convex , then f : > IR -

=
=
Si= [xiyi/s22 = Zy2 No tan
plane at origin.
is CONVEX iff Exe (0 , 1) Ex , yea Find and corresponding
.
2
eigenvalues > 7

u v
, ,
, ,
nv = +
f(xx + (1 xy) = xf(x) + (1 x)f(y)
- -

.
eigenvectors v
,, v.
Note V , +
V
·
A function is if it is convex
Su = V ; (v)
=
convex 1
Sv = <v
;
=
.

on
every line segment in .

· Let &R be open and convex , fineir Hence F(dv , + BV) < x + 32x2 =
.

smooth then Since v, + V then largest value USEFUL INEQUALITIES

-
f is convec iff He is positive semidefinite one. Of F is along largest eigenvalue TRIANGLE (c +
y1< (x) + 1y)
f is strictly convexiff
If is positive definiteon - and lowest is along smallest e. value. BERNOULLI 1 + > (1 + >)" < -1, re(0 , 1)
-
+x
,

·
If fis smooth and strictly convex then it EXP'Le (1 +* 1 + x ,
>1, |=n

can have at most one global minimum

.
For cases in IR3 :
LOGIMIC = [In (1+ x)
,
x-

· If f is convex and for some a EIR" Si = [x? HERMITE y b)sd4(b)

I I
S2 = 24?
↑
global minimum ↓

Siss
Df (a) = 0 then a is a
convex

DIRECTION OF GREATEST INCREASE S33 = [z

and
Let f : U-IR be smooth
Sp Szi = Exiyi
U at U ,
on
, 53 S32533 =
ElGENVALUES
Af(a) = 0 the maximum rate of .

change S13 Sei

= = [xizi Tr (M) = EX ;
of at a is 1xf(a)) and at the
Det (M)
S23 S32 =EYizi
=
=
Toi
direction of Nf(a) ·

GRADIENT DESCENT FUBINI'S THEOREM : DOT PRODUCT

Basic Idea : Rectangle Version : Let D = [a , b]x[d] Gob =
llallIIbIIcoSE
1. x = b be a
rectangle and f : D-IR continuous (2a) · b= < (a b) - =
a .
(9b)
(n + 1 = xn + tnTf(xn) then a (b + c) a= b + a
· =
2
. - C

()y]
Fixed Step Size o
a ((b + c) ((aob) + (a -)

((f(x
· =

, Y) docdy =

·
Optimal Step Size CaoBb = [B(ao b)
1 Set 1.

SideJay
.

.
2 l := ExEI" : x =(n + tDf(xn) ,
tER3 =

.
3 Find minimum of on l

.
4 At that t , get <n+= xn + t0f(xn) PRINCIPALADES :
·

Armijo QEMn(1R) positive definite ,

+
1. Seto choose fixed dE(0 , 1) => D All 1 ; ER
,
.
2 For t , choose t = 1 initially 2) ONB exist

.
3 Halve t until Armijo Condition 3) Diagonalisable
f(xn) f(xn - -
tnXf(x(n)) >, It 18 +(m)4