CONVEX FUNCTIONS

CONVEX OPTIMIZATION PROBLEMS

Convex Optimization Problems

Jhean Eleison Pérez López

UNIVERSIDAD INDUTRIAL DE SANTANDER

Escuela de Matemáticas

24 de octubre de 2023

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

CONVEX FUNCTIONS

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

We begin with a definition of the graph of a real-valued function.

Definition 1.
The graph of f : Ω → R, Ω ⊂ Rn , is the set of points in
Ω × R ⊂ Rn+1 given by

[x, f (x)]T : x ∈ Ω .
{︀ }︀

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Definition 2.
The epigraph of a function f : Ω → R, Ω ⊂ Rn , denoted
epi(f ), is the set of points in Ω × R given by

epi(f ) = [x , 𝛽]T : x ∈ Ω, 𝛽 ∈ R, 𝛽 ≥ f (x )
{︀ }︀

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Definition 3.
A function f : Ω → R, Ω ⊂ Rn , is convex on Ω if its epigraph
is a convex set.

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Teorema 1.1.
If a function f : Ω → R, Ω ⊂ Rn , is convex on Ω, then Ω is a
convex set.

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Teorema 1.2.
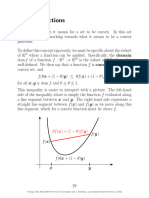
A function f : Ω → R defined on a convex set Ω ⊂ Rn is
convex if and only if for all x, y ∈ Ω and all 𝛼 ∈ (0, 1), we have

f (𝛼x + (1 − 𝛼)y ) ≤ 𝛼f (x) + (1 − 𝛼)f (y ).

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Definition 4.
A function f : Ω → R on a convex set Ω ⊂ Rn is strictly
convex if for all x , y ∈ Ω, x ̸= y , and 𝛼 ∈ (0, 1), we have

f (𝛼x + (1 − 𝛼)y ) < 𝛼f (x ) + (1 − 𝛼)f (y ).

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Definition 5.
A function f : Ω → R on a convex set Ω ⊂ Rn is (strictly)
concave if −f is (strictly) convex.

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Proposition 1.3.
A quadratic form f : Ω → R, Ω ⊂ Rn , given by
f (x ) = x T Qx , Q ∈ Rn×n , Q = Q T , is convex on Ω if and
only if for all x , y ∈ Ω, (x − y )T Q (x − y ) ≥ 0.

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Teorema 1.4.
Let f : Ω → R, f ∈ 𝒞 1 , be defined on an open convex set
Ω ⊂ Rn . Then, f is convex on Ω if and only if for all x , y ∈ Ω,

f (y ) ≥ f (x ) + Df (x )(y − x )

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Teorema 1.5.
Let f : Ω → R, f ∈ 𝒞 2 , be defined on an open convex set
Ω ⊂ Rn . Then, f is convex on Ω if and only if for each x ∈ Ω,
the Hessian F (x ) of f at x is a positive semidefinite matrix.

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Example 1.6.
Determine whether the following functions are convex,
concave or neither:
1. f (x) = −8x 2 ;
2. f (x) = 4x12 + 3x22 + 5x32 + 6x1 x2 + x1 x3 − 3x1 − 2x2 + 15;
3. f (x ) = 2x1 x2 − x12 − x22 .

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

CONVEX OPTIMIZATION
PROBLEMS

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Teorema 2.1.
Let f : Ω → R be a convex function defined on a convex set
Ω ⊂ Rn . Then, a point is a global minimizer of f over Ω if and
only if it is local minimizer of f .

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Lemma 2.2.
Let g : Ω → R be a convex function defined on a convex set
Ω ⊂ Rn . Then, for each c ∈ R, the set

Γc = {x ∈ Ω : g (x ) ≤ c}

is a convex set.

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Corollary 2.3.
Let f : Ω → R be a convex function defined on a convex set
Ω ⊂ Rn . Then, the set of all global minimizers of f over Ω is a
convex set.

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Lemma 2.4.
Let f : Ω → R be a convex function defined on the convex set
Ω ⊂ Rn , and f ∈ 𝒞 1 on an open convex set containing Ω.
Suppose the point x * ∈ Ω is such that for all x ∈ Ω, x ̸= x * ,
we have
Df (x * ) (x − x * ) ≥ 0.
Then, x * is a global minimizer of f over Ω.

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Teorema 2.5.
Let f : Ω → R be a convex function defined on the convex set
Ω ⊂ Rn , and f ∈ 𝒞 1 on an open convex set containing Ω.
Suppose the point x * ∈ Ω is such that for any feasible
direction d at x * , we have

d T ∇f (x *) ≥ 0
Then, x * is a global minimizer of f over Ω.

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Corollary 2.6.
Let f : Ω → Rf ∈ 𝒞 1 , be a convex function defined on the
convex set Ω ⊂ Rn . Suppose the point x * ∈ Ω is such that

∇f (x * ) = 0.

Then, x * is a global minimizer of f over Ω.

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

We now consider the constrained optimization problem

minimize f (x )
subject to h(x ) = 0.

We assume that the feasible set is convex. An example where

this is the case is when

h(x ) = Ax − b.

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Teorema 2.7.
Let f : Rn → R, f ∈ 𝒞 1 , be a convex function on the set of
feasible points

Ω = {x ∈ Rn : h(x ) = 0} ,

where h : Rn → Rm , h ∈ 𝒞 1 , and Ω is convex. Suppose there

exist x * ∈ Ω and 𝜆* ∈ Rm such that

Df (x * ) + 𝜆*T Dh (x * ) = 0T .

Then, x * is a global minimizer of f over Ω.

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Consider the general constrained optimization problem

minimize f (x )
subject to h (x ) = 0
g (x ) ≤ 0.
As before, we assume that the feasible set is convex. This is
the case if, for example, the two sets {x : h(x ) = 0} and
{x : g (x ) ≤ 0} are convex.
We now prove that the Karush-Kuhn-Tucker (KKT) condition
is sufficient for a point to be a minimizer to the above problem.

Jhean Pérez Convex Optimization Problems

 CONVEX FUNCTIONS
CONVEX OPTIMIZATION PROBLEMS

Teorema 2.8.
Let f : Rn → R, f ∈ 𝒞 1 , be a convex function on the set of
feasible points

Ω = {x ∈ Rn : h(x ) = 0, g (x ) ≤ 0} ,

where h : Rn → Rm , g : Rn → Rp , h, g ∈ 𝒞 1 , and Ω is convex.

Suppose there exist x * ∈ Ω, 𝜆* ∈ Rm , and 𝜇* ∈ Rp , such that
1. 𝜇* ≥ 0;
2. Df (x * ) + 𝜆*T Dh (x * ) + 𝜇*T Dg (x * ) = 0T ; and
3. 𝜇*T g (x * ) = 0.
Then, x * is a global minimizer of f over Ω.

Jhean Pérez Convex Optimization Problems