Professional Documents
Culture Documents
Limits Hints 1
Limits Hints 1
Uploaded by
MBWAMaira ShoaibOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Limits Hints 1
Limits Hints 1
Uploaded by
MBWAMaira ShoaibCopyright:
Available Formats
Marathon Academy Kolkata
Chapterwise Solutions
Subjects Total Marks Duration No. of Questions
Mathematics 400 Marks 3 Hrs30 Mins 100 Questions
Instructions
1. Total duration of test is 3 hours 30 minutes.
2. Total number of questions in the test is 100.
3. Total number of sections in the test is 1.
4. Section 1 is Single Option Correct consisting of 100 questions.
Single Option Correct
Single Option Correct 100 Questions: 400 Marks
Q.2 4 Marks
Q.1 4 Marks
The function , has a local
A function is said to be a rational function, if , where and
minimum at , then
are polynomials such that , then
A) is any even number
A)
B) is an odd number
B) and does not exist
C) is odd prime number
C) both first option and second option are true D) is any natural number
D) both first option and second option are false Explanation:
Explanation:
A function f is said to be a rational function, if Differentiating we get
, where and are polynomials such that .
Then,
If there are two scenarios - when and when
So, is the critical point and at the critical point sign of the first derivative
.
must be changed
In case the limit does not exist. In case , we can write
Since, ,
, where is the maximum of powers of in
. So the expression is
always positive.
Similarly, as . Now, if , then
the sign of depends upon the expression .
So, if is odd then is always positive and when is even then
changes sign,
So, can be any even numbers.
If , the limit is not defined.
Marathon Academy Kolkata
Q.3 4 Marks Q.4 4 Marks
Evaluate
Let the function be defined by ,then
A)
A)
B)
B)
C)
C)
D)
D) doesn't exist Explanation:
Given
Explanation:
Substituting limit values we get,
Given
Now Left hand limit,
Its in in-determinant form,apply l-hospital rule.
Right hand limit,
Again it is in in-determinant form,apply l-hospital rule,
Therefore, doesn't exist.
Hence
Marathon Academy Kolkata
Q.5 4 Marks Q.6 4 Marks
Let
If then equation of circle whose centre is
f θ tan θ tan θ ... tan θ tan θ
tan θ and radius unit is
π
. The left hand limit of f() as θ is A)
A) 1900
B)
B) 2000
C)
C) 2100
D) none of these
D) 2200
Explanation:
Explanation:
f θ tan θ tan θ ... tan θ ta
tan θ
By binomial theorem, required equation is
tan C C tan ....
C tan θ C tan θ C tan θ
tan θ
tan θ tan θ
C C tanθ ... C tan θ C C tanθ
tanθ
lim
π tan θ
θ
lim C C tanθ ... C tan θ C tan θ C tan
π tan θ
x
C lim tanθ
π
θ
Similarly ;
tanθ
lim lim tanθ,
π tan θ π
θ θ
tanθ
lim lim tanθ
π tan θ π
θ θ
...............................................................
...............................................................
tanθ
lim lim tanθ
π tan θ π
θ θ
On adding all these terms; we get
lim f θ ... lim tanθ
π π
θ θ
lim d tan
lim f θ ...
π
θ
Marathon Academy Kolkata
Q.7 4 Marks Q.8 4 Marks
For the function Consider the following statements:
is an indeterminate form (where denotes greatest integer
Which of the flowing is true?
∞ function).
A) does not exist
does not exist.
B) does not exist
State, in order, whether are true or false
C) Both limits exist and
A)
D) Both limits exist and B)
Explanation: C)
∞ D)
We know,
∞ Explanation:
which is not an indeterminate form.
Given,
∞
For
∞
As the domain of is will have a finite value lying between
at all real numbers.
For ,
Foe ,
=log 3
It is clear that both limits exist and
Marathon Academy Kolkata
Q.9 4 Marks Q.11 4 Marks
The value of is equal to
If , the equation whose roots are and
A) , is
B) A)
C) B)
D) C)
Explanation: D)
Explanation:
Obviously it is form
We know the formulae
Multiply and divide by and multiply divide the denominator by
Therefore, and are the roots of the equation.
Hence, the required equation is
sum of roots product of roots
Divide numerator and denominator by we get
Now by applying above limit formulae we get
Q.10 4 Marks
is equal to
A)
B)
C)
D)
Explanation:
First define the expansion of logarithmic series,
where ,
Then,
Marathon Academy Kolkata
Q.12 4 Marks Q.13 4 Marks
The value of is If and then
A) A) is equal to
B) is equal to
B)
C) is equal to
D) Does not exist
C)
Explanation:
D)
If is in the left neighbourhood of
Explanation:
Given,
If is in the right neighbourhood of
Replace by . Hence does not exist.
Q.14 4 Marks
Thus,
Let and where is a continuous function. Then
exists if
A) is any polynomial
We know,
B)
C)
D)
Explanation:
Now, It is given that
exists if or . If , then and
. Thus doesn't exist in this case.
Marathon Academy Kolkata
Q.15 4 Marks Q.17 4 Marks
If and where ∞
, then which of the following statement is true - equals to
A) Neither nor exists A)
B) exists and does not exists
B)
C) does not exists and exists
C)
D) None of these
D)
Explanation:
Explanation:
We know and
Given
∞
and
does not exist and exists
∞
Hence, (3) is the correct option.
Q.16 4 Marks
Evaluate
∞
A)
B)
C) ∞
D)
Explanation:
Given ∞
Plugging in the limiting value,we get
This is an indeterminant form,so can use l'Hospital's rule
Hence
Marathon Academy Kolkata
Q.18 4 Marks Q.19 4 Marks
Let and be two functions such that and exist. Then, If be a quadratic equation that and
which of the following is incomplete? then is equal to:
A) A)
B)
B)
C)
C)
D) None of these
D) Explanation:
Given that is a quadratic equation.
Explanation:
and are two roots of .
Let and be two functions such that both and exist.
Let
Then,
(i) Limit of sum of two functions is sum of the limits of the functions i.e., also
(ii) Limit of difference of two functions is difference of the limits of the
functions, i.e.,
So
Now,
(iii) Limit of product of two functions is product of the limits of the functions,
i.e.,
(iv) Limit of quotient of two functions is quotient of the limits of the functions Let , then
(whenever the denominator is non-zero), i.e.,
if
Hence, option is not correct.
Marathon Academy Kolkata
Q.20 4 Marks Q.22 4 Marks
If , (where [.] represents GIF), then : If then
A) A)
B) B)
C)
C)
D)
D) Explanation:
Given limit is in indeterminate form.
Explanation:
Therefore first taking L.C.M., we get
if x > 0,
Now, for limit to be finite non zero, degree of numerator = degree of
if x < 0, denominator.
Therefore, and .
Q.23 4 Marks
Let denotes greatest integer function and then
A) does not exist
B) is continuous at
C) is not differentiable at
D)
4 Marks Explanation:
Q.21
Given,
is equal to
As we know is increasing in
A)
In the above range of ; and
B)
C)
D)
Explanation:
where is continuous at
and And also limit exists.
is continuous at
Now,
Marathon Academy Kolkata
Q.24 4 Marks
If , Therefore,the correct answer is
then find the value of .
Q.25 4 Marks
A)
The value of
B) A)
C) B)
D) C)
Explanation:
D) None of these
Given
Explanation:
Given
Since,
For
Let general term for sequence be
form
By using L.Hospital Rule: Thus,
Now .
Marathon Academy Kolkata
Q.26 4 Marks Q.28 4 Marks
If exists, then The value of , is
A) both and must exist A)
B)
B) need not exist but exist
C)
C) neither nor may exist
D) None of these
D) exists but need not exist
Explanation:
Explanation:
We are justifying the answer with an example,
Let and then both and do
not exist,
( is an oscillatory function, limit does not exists
but exists
neither nor may exist
Q.27 4 Marks
, where denotes the greatest integer less
than or equal to is
A)
B)
C)
D)
Explanation:
For
( is positive).
Therefore,
Marathon Academy Kolkata
Q.29 4 Marks Q.30 4 Marks
If and then
A) A)
B)
B)
C)
C)
D)
D)
Explanation:
Explanation:
It is given that,
Let,
Apply L'hospital rule, We know that:
Again, apply L'hospital rule,
Multiplying and dividing by:
Now
Use:
Apply L'hospital rule,
Again, apply L hospital rule,
Taking common from all the brackets, we get:
or,
From equation and Now, put limit , so we get:
Marathon Academy Kolkata
Q.31 4 Marks Q.32 4 Marks
If : , R and lim nf and f(0) = 0. Find the value of is equal to
n
n
A)
lim n cos n given that lim cos
n n
n n
B)
A)
C)
B)
D)
C)
Explanation:
D)
Explanation:
Here, lim n cos n
n
n
......breaking
lim n cos lim nf ; (100 terms)
n n n
n n
where cos
n n n
Putting in the form of standard limit and, applying:
given lim nf
n
n
lim n cos n ...(i)
n
n
where x x cos x ,
x x cos x
x
...(ii)
From Eqs. (i) and (ii)
lim n cos n
n
n
Marathon Academy Kolkata
Q.33 4 Marks Q.34 4 Marks
If is the distance between orthocentre and circumcentre of triangle with
The value of is:
vertices , then is
A) A)
B) B)
C)
C)
D) Does not exist
D) Does not exist.
Explanation:
Explanation:
Let are the vertices of the given triangle, then
Given that:
is equilateral.
And we know that in equilateral triangle all centres coincide.
So, required distance
Rationalising the Given Expression, we get:
will not exist as we know that greatest integer function does not
exist at all integers.
which gives at
and at
So, the limit does not exist.
Marathon Academy Kolkata
Q.35 4 Marks Q.36 4 Marks
Which of the following limit exists finitely? is equal to
A) A)
B)
B)
C)
D)
C)
( where denotes the greatest integer
E)
function )
Explanation:
D) none of these
Let's
Explanation:
(1)
Hence, limit does not exist finitely.
(2)
L.H.L.
R.H.L.
L.H.L. R.H.L.
Limit does not exist
(3)
Here, (exact value)
Hence, limit exist finitely.
Marathon Academy Kolkata
Q.37 4 Marks Q.38 4 Marks
The value of is: (where denotes the is, where represents the integral part of .
greatest integer function.) A)
A)
B)
B)
C)
C)
D)
D) None of these
Explanation:
Explanation:
Since, , where is an integer We know
and
Therefore,
Q.39 4 Marks
is
A)
Since fractional part of any number lies between and .
B)
Therefore, C)
D)
Explanation:
We have,
...( form)
Now substituting
Marathon Academy Kolkata
Q.40 4 Marks Q.41 4 Marks
If denotes greatest integer less than or equal to then
is equal to
A) exists and it equals
A)
B) B) exists and it equals
C) C) does not exist because
D) does not exist because left hand limit is not equal to right hand limit
D)
Explanation:
Explanation:
Let
We know that , where is integral part
of and is fractional part of and also
Using
Also,
Put
As
Now,
( , since each part of the numerator is less
than and total terms are there in numerator, so the numerator is less
than and )
So limit does not exist at
Q.42 4 Marks
are real and distinct roots of , then
is :
A)
B)
C)
D) None of these
Explanation:
are roots of equation
( form)
Marathon Academy Kolkata
Q.43 4 Marks Q.45 4 Marks
x
e x
Let and then as ∞ lim equals, where is fractional part function and I is an integer
x x
A) exists but does not exist
∞ ∞
A)
B) does not exist but exists
∞ ∞ B) e – 2
C) Both the sequences do not have limits C) I
D) Both the sequence have limits D) Does not exisst
E) Explanation:
Explanation: Use
For fraction part here
Given, .......(i)
h
e h
⇒lim
h
And, .....(ii) h
⇒e
Now, from Equation. (i), we get
∞ 4 Marks
Q.46
does not exist
If then
And
A) exists for
exist.
B) exists and finite for
Q.44 4 Marks
C) does not exist for any value of
The value of is equal to
A) cannot be determined
D)
B) Explanation:
C) For
( any value between to )
D)
For
Explanation:
(any value between to )
Given Limit
Marathon Academy Kolkata
Q.47 4 Marks Q.48 4 Marks
If
Evaluate: , (where )
∞
where , then A) sin x
A)
B) log(2 + x) + sin x
B)
C) sin x – log(2 + x)
C) D) log 2 + sinx
Explanation:
D)
Explanation:
∞
Given:
=
∞
= sinx
By differentiating w.r.t. we get:
Q.49 4 Marks
x , if x
If f x and g(x)= f(|x|) + |f(x)l, then in [-3,2]
2x , if x
A) lim g x
x
B) lim g x
x
Therefore,
C) g(x) is discontinuous at three points
By using this value in , we get
D) None of these
Explanation:
lim g x lim f x f x lim f x f x lim x x
Now by applying We get: x x x x
lim g x lim f x f x & is
x x
{As } continuous at is discontinuous at
As.L.H.S. is of form. So,by applying L.Hospital rule we get :
Marathon Academy Kolkata
Q.50 4 Marks Q.51 4 Marks
At the function has
is equal to (where represents greatest integer function)
A) A minimum
A)
B) A discontinuity
B)
C) A point of inflexion
C)
D) A maximum
D) does not exist.
Explanation:
Explanation:
Given,
We have,
At t = 0, first we will check continuity of the function.
Now,
Let if
As or
And
Since,
So, the function is continuous at t = 0
Now, we check the function is maximum or minimum
′′
and
For maximum or minimum value of , put
Now,
[using L' Hospital rule]
So, function f(t) is maximum at t = 0
Marathon Academy Kolkata
Q.52 4 Marks Q.53 4 Marks
Select the correct answer from the given alternatives. The graph of the function is
A)
B)
C) A)
D)
Explanation:
To find:
Let,
B)
C)
D)
Explanation:
We have,
Let , then
When then , therefore
Marathon Academy Kolkata
And, it is the equation of -axis.
Q.55 4 Marks
Q.54 4 Marks , (where denotes the fractional part of ) is equal to:
Select the correct answer from the given alternatives.
A)
B)
A)
B) C)
D)
C)
Explanation:
D) Let,
Explanation:
To find:
Let,
Given limit is of indeterminate form which can be solved using
technique,
If , then
or,
Hence, the value of limit
or,
Using
Hence,
∞
Q.56 4 Marks
Let such
that . Also
then equals
A)
B)
C)
D)
Explanation:
Marathon Academy Kolkata
Q.57 4 Marks Q.60 4 Marks
If then The value of is
A)
A)
B)
B) C)
D)
C)
Explanation:
D) Let
Explanation:
where, as
. Now,
Q.58 4 Marks
Evaluate : , by using formula.
A)
B)
C)
D)
Explanation:
form
Q.61 4 Marks
If (finite), then:
A)
B)
C)
D)
Q.59 4 Marks
Explanation:
If then
A)
This is of the form . Applying L' Hospital rule,
B)
(on putting )
C)
Therefore, , because for the limit to exist, the function has to be of
D) the form so as to be able to apply the L' Hospital rule.
Explanation:
So,
Given,
This limit will exist, if
Marathon Academy Kolkata
Q.62 4 Marks Q.63 4 Marks
If be a differentiable function at satisfying and
Let , find the quadratic equation whose roots are
then the value of
and .
A)
A)
B) B)
C)
C)
D) D)
Explanation: Explanation:
Given,
This is in form. Therefore, applying the L' Hospital rule, we have
and
Now, , so for we have,
Therefore, the quadratic equation whose roots are and is
Therefore, by ,
Q.64 4 Marks
Evaluate:
A)
B)
C)
D)
Explanation:
Let,
Marathon Academy Kolkata
Q.65 4 Marks Q.67 4 Marks
The limit of the interior angle of a regular polygon of sides as is Which of the following limit does NOT exist?
A) A)
∞
B)
B)
C)
C)
D)
Explanation: D)
The interior angle of a regular polygon is Explanation:
It is clear that, the limit of the interior angle of a regular polygon of sides as
is or
By putting we get
Q.66 4 Marks
The value of is
We know that,
A)
B)
C)
D)
Explanation:
We know that the expansion of and also
.
Clearly, this limit does not exists as .
Limiting value is zero.
Marathon Academy Kolkata
Q.68 4 Marks Q.70 4 Marks
m
k
x k If and , such that , then
If k lim m
, then k is (m > 101)
x x
A) must not be divisible by
A) 10 B) is divisible by or is neither divisible by nor by
B) 102 C) must be divisible by but not necessarily by
C) 103 D) None of these
Explanation:
D) 104
Given,
Explanation:
It is given that
x k
m
The above is possible when,
k
k lim m
x x
That is,
Divide numerator and denominator by xm, we have
k m
k x
k lim And,
x
xm
...upto 1000 times
Hence,
= 1000 = 103 and
So, is divisible by both, and . Which means, is divisible by LCM of
So, correct option is 103.
, which is .
Hence, must be divisible by but not necessarily by its multiples.
Q.69 4 Marks
The function :
A) Has a maxima but no minima.
B) Has a minima but no maxima.
C) Has both a maxima and minima.
D) Is monotonic.
Explanation:
(can be verified)
Also is increasing for all ,
(can be verified)
Marathon Academy Kolkata
Q.71 4 Marks Statement is true, Statement is also true; Statement is the
A)
For the following questions, choose the correct answer from the codes correct explanation of Statement
and defined as follows:
Statement does not exist, (where denotes the greatest integer
function) Statement is true. Statement is also true; Statement is not the
B)
correct explanation of Statement .
Statement does not exist.
C) Statement is true. Statement is false.
D) Statement is false. Statement is true.
Explanation:
For the statement
Let
If then
Using squeeze play theorem ,
If then
Using squeeze play theorem ,
Thus exists.
Therefore the statement is false.
For the statement
Let
the limit does not exist.
Therefore, the statement is true.
Marathon Academy Kolkata
Q.72 4 Marks Q.73 4 Marks
is equal to: The value of is equal to
A)
A)
B)
C)
B)
D)
Explanation:
C) After rationalization,
D)
Explanation:
Let
Using binomial expansion for any index,
Then
And let
Using logarithmic expansion,
then
Now
Marathon Academy Kolkata
Q.74 4 Marks Q.75 4 Marks
The value of is:
Let . Then which of the following can best
represent the graph of ?
A)
B)
A)
C)
D)
Explanation:
Given that:
B)
Taking common, we get:
Let: C)
Multiply and Divide by
We get,
D)
Taking common from the denominator, we get:
Explanation:
Obviously, .
Hence, is continuous at .
Put the Value of Equation in Equation .
Therefore,
Let .
So,
∞
Marathon Academy Kolkata
Q.76 4 Marks Q.77 4 Marks
Let where denotes the integer not greater than Then
for any integer is equal to
A) is continuous at
A)
B) exists and is equal to
B)
C) exists but is not equal to
C)
D) is differentiable at
Explanation: D) None of these
For and and for Explanation:
and Thus
or and so
As
But Hence
exists but is not equal to
(From equation )
Marathon Academy Kolkata
Q.78 4 Marks Q.80 4 Marks
equals
The value of is equal to
A)
A)
B)
B)
C)
C)
D)
D)
Explanation:
Explanation:
Rationalising the numerator,
Q.79 4 Marks
_____
A)
B)
C)
Using
D)
Explanation:
Let
as
Applying Trigonometric limits property,
Marathon Academy Kolkata
Q.81 4 Marks Q.83 4 Marks
Evaluate:
∞
If is continuous at then which one
A)
B)
is correct
A) C)
D)
B)
Explanation:
C)
∞
D) None of these
Explanation:
∞
Q.84 4 Marks
Also If , where denotes the greatest integer function,
then find .
A)
Thus we must have B)
So and is any real number. C)
D) Limit does not exist.
Q.82 4 Marks
E)
What is the value of , if denotes the fractional part of x
Explanation:
A)
Given,
B)
C)
D)
Explanation:
LHL ≠
So, the limit does not exist.
Marathon Academy Kolkata
Q.85 4 Marks Q.88 4 Marks
As , then for the function , is called
Let where is the fractional part of , then
A) limit of the function.
A) has value
B) value of the function.
B) has value
C) absolute value of the function.
C) has value
D) none of these.
D) has value
Explanation:
Explanation:
As , then for the function , is called limit of the
As function.
Similarly as As , then for the function , is called value of the
function.
As , then for the function , is called absolute value
of the function.
Q.86 4 Marks
The value of is equal to:
A) 26
B) 16
C) -14
D) -40
Explanation:
Q.87 4 Marks
Let Then the set of values of for which
, is given by -
A)
B)
C)
D)
Explanation:
if and only if,
Marathon Academy Kolkata
Q.89 4 Marks Q.90 4 Marks
is equal to
A)
be a continuous function, then
A)
B)
B)
C)
C)
D) none of these.
D)
Explanation:
Explanation:
We have,
(i) If then
(ii) If then
(iii) If then
Let and , then we have
(iv) If then
is continuous at if and
is the only correct option.
Now, let , then we have
Q.91 4 Marks
The limit of as tends to zero equals
A) zero.
B) one.
but as so, put , then
C) two.
D) three.
Explanation:
Given function . Observe that as takes value very close to
, the value of also approaches to .
NOTE:
We say
(i.e., the limit of as tends to zero equals zero).
Put
Marathon Academy Kolkata
Q.92 4 Marks Q.94 4 Marks
The limiting value of at is The value of equals
A) A)
B) B)
C) C)
D) none of these.
D)
Explanation:
Explanation:
is of the form Let
Applying L′ Hospital rule, we get
Applying L′ Hospital rule, we get
is of the form
By L'Hospital's rule,
Q.95 4 Marks
Which of the following condition is satisfied by , if exists finitely?
Q.93 4 Marks
A)
For each let be the greatest integer less than or equal to Then,
B)
C)
A) does not exist
D) none of these
Explanation:
B) equals
C) equals Since numerator is a quadratic function, the degree of denominator should be
greater than or equal to two for the limit to exist finitely.
D) equals For ,
Explanation:
∞
Let For ,
∞
Now,
For ,
Therefore, the limit will give a finite value if .
Marathon Academy Kolkata
Q.96 4 Marks Q.98 4 Marks
Set of all values of such that is a non-zero and finite At the function is
A) Continuous
number, when is
A) B) Discontinuous
C) Differentiable
B)
D) Non-zero
C) Explanation:
D) Given,
Explanation:
Now, RHL
for limit to be finite,
And LHL
RHL LHL
is discontinuous at
Q.97 4 Marks
α α
If , where , then
is equal to:
A)
B)
C)
D)
Explanation:
Using Eular's Theorem we get,
Marathon Academy Kolkata
Q.99 4 Marks Q.100 4 Marks
If , then the value/values of The value of is.
A) A)
B) B)
C) C)
D) D)
Explanation: Explanation:
sin sin sin
We have lim Let
Since numerator when ,
Denominator must approach .
Factorising both numerator and denominator, we get
sin sin sin
Now, lim
sin sin
sin cos
lim
sin
sin
sin sin
lim sin
cos .
sin
lim
cos
lim (using L’ Hospital’ rule)
sin
lim
sin
lim
for all
Marathon Academy Kolkata
Marathon Academy Kolkata
You might also like
- Iso 11070 PDFDocument28 pagesIso 11070 PDFHemant SharmaNo ratings yet
- Market Profile's: Basic ComponentsDocument108 pagesMarket Profile's: Basic Componentskakadiya piyush100% (4)
- Continuty & Differentiabilyty-Hints-1Document39 pagesContinuty & Differentiabilyty-Hints-1tryambakabanerjeeNo ratings yet
- Continuity & Differentiabilyty-Ques-1Document12 pagesContinuity & Differentiabilyty-Ques-1tryambakabanerjeeNo ratings yet
- Workshop CH 4Document17 pagesWorkshop CH 45fyqv62kytNo ratings yet
- Limits & DerivativesDocument52 pagesLimits & DerivativesKartik AggarwalNo ratings yet
- 1.6.linear TransformationDocument8 pages1.6.linear TransformationSai RenuNo ratings yet
- Lecture Note On Mathematical Methods I MDocument66 pagesLecture Note On Mathematical Methods I MAyomikunNo ratings yet
- Ellipse Ques 2Document12 pagesEllipse Ques 2Biswarup SadhukhanNo ratings yet
- BC 1 Limits 1.4 Continuity IVT POSTDocument14 pagesBC 1 Limits 1.4 Continuity IVT POSTCatrinaNo ratings yet
- Lec 41Document23 pagesLec 41Dr. B. Srinivasa Rao Professor, EEE DepartmentNo ratings yet
- Tmctest 1 RDocument1 pageTmctest 1 Rcodewizard.19No ratings yet
- Good Day Students!! )Document46 pagesGood Day Students!! )nino sulitNo ratings yet
- Radical Equations: Subtitle Goes HereDocument27 pagesRadical Equations: Subtitle Goes HereKristine HensonNo ratings yet
- The Laplace TransformDocument34 pagesThe Laplace Transformjkligvk. jukjNo ratings yet
- Point-Wise Convergence and Uniform ConvergenceDocument3 pagesPoint-Wise Convergence and Uniform ConvergenceHưng PhạmNo ratings yet
- ICC Cricket World Cup 2019 - Live Cricket Scores, Match Schedules, Points, News, ResultsDocument1 pageICC Cricket World Cup 2019 - Live Cricket Scores, Match Schedules, Points, News, ResultsmsikkNo ratings yet
- Real NumbersDocument125 pagesReal NumbersVernon MonteiroNo ratings yet
- 20Document14 pages20VivekRouthNo ratings yet
- Polynomial Rings: Example. (Polynomial Arithmetic) (A) ComputeDocument10 pagesPolynomial Rings: Example. (Polynomial Arithmetic) (A) Computecường Nguyễn anhNo ratings yet
- Lesson 2 Constant and VariableDocument2 pagesLesson 2 Constant and VariableLyrazelle FloritoNo ratings yet
- Chapter 5Document15 pagesChapter 5yohannes lemiNo ratings yet
- Lec 4Document20 pagesLec 4pbhanududiNo ratings yet
- Ncert Solutions Class 12 Maths Chapter 6 Ex 6 5Document53 pagesNcert Solutions Class 12 Maths Chapter 6 Ex 6 5sparklingstar7766No ratings yet
- Answers & Solutions: Part Test (Pt-02)Document5 pagesAnswers & Solutions: Part Test (Pt-02)Aravind VnNo ratings yet
- UntitledDocument3 pagesUntitledGanesh KarthiNo ratings yet
- Prealgebra 5th Edition Lial Hestwood Solution ManualDocument79 pagesPrealgebra 5th Edition Lial Hestwood Solution Manualmichael100% (34)
- Solution Manual For Prealgebra 5Th Edition Lial Hestwood 0321845021 9780321845023 Full Chapter PDFDocument36 pagesSolution Manual For Prealgebra 5Th Edition Lial Hestwood 0321845021 9780321845023 Full Chapter PDFkenneth.shook898100% (18)
- Functional Analysis Prof. P. D. Srivastava Department of Mathematics Indian Institute of Technology, KharagpurDocument15 pagesFunctional Analysis Prof. P. D. Srivastava Department of Mathematics Indian Institute of Technology, KharagpurKofi Appiah-DanquahNo ratings yet
- Grade 9 - Unit 1 NotesDocument29 pagesGrade 9 - Unit 1 Notesapi-2889220720% (1)
- Week 11 Circular Functions 1 1Document26 pagesWeek 11 Circular Functions 1 1Kimberly Joy ArroyoNo ratings yet
- Triangle Congruence: Mathematical SystemDocument31 pagesTriangle Congruence: Mathematical SystemKyle Cada IINo ratings yet
- Applied Math IIDocument80 pagesApplied Math IIabyu adaneNo ratings yet
- 2011 미분적분학1 중간고사Document2 pages2011 미분적분학1 중간고사신지안No ratings yet
- Limits and Real NumbersDocument10 pagesLimits and Real NumbersSomya ShuklaNo ratings yet
- Interchanging of Limit and Basic Properties of FunctionsDocument14 pagesInterchanging of Limit and Basic Properties of Functionsaye pyoneNo ratings yet
- Math 1 Unit 1 Chaoter 1 The Language of AlgebraDocument18 pagesMath 1 Unit 1 Chaoter 1 The Language of AlgebraPahilagao NelsonNo ratings yet
- 20498Document2 pages20498Kateryna TernovaNo ratings yet
- Exercises and SolutionDocument11 pagesExercises and SolutionQuang Đức NguyễnNo ratings yet
- Introductory Calculus: Prepared By: Kaydene ThomasDocument17 pagesIntroductory Calculus: Prepared By: Kaydene ThomasBabNo ratings yet
- 11 Sampling and AliasingDocument11 pages11 Sampling and AliasingAbhinav Virat BhagatNo ratings yet
- Lecture # 11 (Continuous Functions and Introduction To Derivatives)Document35 pagesLecture # 11 (Continuous Functions and Introduction To Derivatives)Arfaat SanitaryNo ratings yet
- Math Grade 7 DLL Q2 W7 JANDocument4 pagesMath Grade 7 DLL Q2 W7 JANthalia alfaroNo ratings yet
- Diophantine Equations (Ioqm/Prmo) Linear Combinations: Sum of Fourth PowersDocument5 pagesDiophantine Equations (Ioqm/Prmo) Linear Combinations: Sum of Fourth PowerspiyushNo ratings yet
- Lano Itarr I S I FDocument3 pagesLano Itarr I S I Fyoonjr90No ratings yet
- 2.2 Sub Chapter NotesDocument2 pages2.2 Sub Chapter NotesMe, Myself and INo ratings yet
- American Online Invitational Mathematical Exam Results - AlanchungDocument16 pagesAmerican Online Invitational Mathematical Exam Results - AlanchungAlan ChungNo ratings yet
- KSSM Mathematics Form4 Chapter 1Document32 pagesKSSM Mathematics Form4 Chapter 1LEW XIAO HUI -No ratings yet
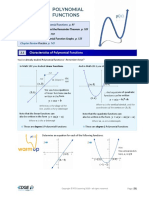
- 2.1 - Characteristics of Polynomial Functions Math 30-1Document14 pages2.1 - Characteristics of Polynomial Functions Math 30-1Math 30-1 EDGE Study Guide Workbook - by RTD LearningNo ratings yet
- 01 Functions Revision Notes QuizrrDocument90 pages01 Functions Revision Notes QuizrrDhairya SharmaNo ratings yet
- Chapter 4 Applications of Derivative: DefinitionDocument8 pagesChapter 4 Applications of Derivative: DefinitionMohammed AlwazeerNo ratings yet
- Art of Problem SolvingDocument20 pagesArt of Problem SolvingdavlatovsurobNo ratings yet
- Lec 33Document16 pagesLec 33Win Alfalah NasutionNo ratings yet
- 1 FunctionsDocument89 pages1 Functionstusharfiitjee80No ratings yet
- CO4 - Applications of Differentiation and Introduction To IntegrationDocument93 pagesCO4 - Applications of Differentiation and Introduction To IntegrationYhel TrinidadNo ratings yet
- Continuity and DifferentiabilityDocument134 pagesContinuity and Differentiabilitysavaliyaabhi248No ratings yet
- Maths 4Document79 pagesMaths 4Yoel SisayNo ratings yet
- Lecture 4 PDFDocument10 pagesLecture 4 PDFNarendran KumaravelNo ratings yet
- Sol 4Document9 pagesSol 4sunsms0108No ratings yet
- Lec 35Document19 pagesLec 35JHAVERI RONAK KIRTIKUMARNo ratings yet
- Dispersion Lab (Geotechnical)Document6 pagesDispersion Lab (Geotechnical)Henock ShewasemaNo ratings yet
- AIMER - Mathematical Seminar Contest - 2022Document6 pagesAIMER - Mathematical Seminar Contest - 2022Trash SinghNo ratings yet
- Optical Rheometry of Complex Fluids FullerDocument283 pagesOptical Rheometry of Complex Fluids FullerClive Delos ReyesNo ratings yet
- NewDocument3 pagesNewAngelica P. CaingcoyNo ratings yet
- BMATE201Document6 pagesBMATE201shashistudy2125No ratings yet
- Centrifugal Fans With Backward-Curved and Forward-Curved BladesDocument8 pagesCentrifugal Fans With Backward-Curved and Forward-Curved BladesjcbobedaNo ratings yet
- Pertemuan: 3 Lembaran Kerja Iii Mata Kuliah Kepemimpinan SKS: 2 Kode: Hari/ Tanggal: Waktu: 10'Document3 pagesPertemuan: 3 Lembaran Kerja Iii Mata Kuliah Kepemimpinan SKS: 2 Kode: Hari/ Tanggal: Waktu: 10'Rahma disaNo ratings yet
- Articulo 5Document9 pagesArticulo 5Elizabeth ManobandaNo ratings yet
- Numerical Modelling of ShotcreteDocument435 pagesNumerical Modelling of Shotcreteaecom2009No ratings yet
- PhysRevLett 128 134101Document5 pagesPhysRevLett 128 134101yejh2219No ratings yet
- Piled Raft A New Foundation Design PhiloDocument10 pagesPiled Raft A New Foundation Design Philodhan singhNo ratings yet
- Chapter 3rd GASES MCQsDocument7 pagesChapter 3rd GASES MCQsbushra3ansari25% (4)
- Chapter 5 - Pressure Vessels: Sr. No. QuestionsDocument5 pagesChapter 5 - Pressure Vessels: Sr. No. Questionsdarshit dadhaniyaNo ratings yet
- Heat Input CalcsDocument3 pagesHeat Input CalcsScott TrainorNo ratings yet
- Ce198 Fluid Mechanics PDFDocument10 pagesCe198 Fluid Mechanics PDFLisa Valois PedrigalNo ratings yet
- Dalton's Law of Partial PressureDocument4 pagesDalton's Law of Partial PressureAgyao Yam FaithNo ratings yet
- Rotary TillerDocument10 pagesRotary TillerJohn Paulo PeridoNo ratings yet
- MK Series Geared Motor 20-8-2013Document104 pagesMK Series Geared Motor 20-8-2013Zahoor AhmedNo ratings yet
- Operator ExamDocument11 pagesOperator ExamFazeel A'zamNo ratings yet
- ks3 Science 2003 Level 5 7 Paper 2Document32 pagesks3 Science 2003 Level 5 7 Paper 2pwebb661919No ratings yet
- General Chemistry q1Document57 pagesGeneral Chemistry q1Dianna Rose QuintoNo ratings yet
- Group 1 - Section 4 - Full ReportDocument18 pagesGroup 1 - Section 4 - Full ReportEliya AiyaniNo ratings yet
- Sag and Tension Calculations For Cable and Wire Spans Using Catenary FormulasDocument8 pagesSag and Tension Calculations For Cable and Wire Spans Using Catenary Formulassamadi88100% (1)
- BEE Module 4 Mesh AnalysisDocument16 pagesBEE Module 4 Mesh AnalysisCharlie OrencilloNo ratings yet
- Mechanical Measurements and Control System-1-194 - 1-97 PDFDocument97 pagesMechanical Measurements and Control System-1-194 - 1-97 PDFElangoNo ratings yet
- Paper 2116 (R1) PDFDocument18 pagesPaper 2116 (R1) PDFShantanu BhattacherjeeNo ratings yet
- Sensor Data Fusion Using Kalman Filter: August 2000Document8 pagesSensor Data Fusion Using Kalman Filter: August 2000pruebaNo ratings yet
- 02 Machine Tool, Automation & Metrology Mechanical Engineering ME 3201 E3/II 23-12-2012Document3 pages02 Machine Tool, Automation & Metrology Mechanical Engineering ME 3201 E3/II 23-12-2012Chaitanya ReddyNo ratings yet