Pre-Calculus _ Chapter 5

5.1: Polynomial Functions and Models

Objectives:
1- Identify the Real Zeros of Polynomial Functions and Their Multiplicity.
2- Analyze the Graph of a Polynomial Function.

1- Identify the Real Zeros of Polynomial Functions and their multiplicity.

Remark: The degree of the polynomial function is the largest power of 𝒙𝒙.
Definition:
• A Polynomial Function is a function of the form

𝒇𝒇(𝒙𝒙) = 𝒂𝒂𝒏𝒏 𝒙𝒙𝒏𝒏 + 𝒂𝒂𝒏𝒏−𝟏𝟏 𝒙𝒙𝒏𝒏−𝟏𝟏 + ⋯ + 𝒂𝒂𝟏𝟏 𝒙𝒙 + 𝒂𝒂𝟎𝟎

where 𝑎𝑎𝑛𝑛, 𝑎𝑎𝑛𝑛−1 , … … . . , 𝑎𝑎1 , 𝑎𝑎0 are real numbers, 𝑛𝑛 is a nonnegative integer and 𝑥𝑥 is the
variable of the function. The domain of a polynomial function is the set of all real
numbers.

Definition:
If 𝑓𝑓 is a function and 𝑟𝑟 is a real number for which 𝑓𝑓(𝑟𝑟) = 0, then 𝑟𝑟 is called a real zero
of 𝑓𝑓.
𝑟𝑟 is a real zero of a polynomial function 𝑓𝑓.
𝑟𝑟 is an 𝑥𝑥-intercept of the graph of 𝑓𝑓.
𝑥𝑥 − 𝑟𝑟 is a factor of 𝑓𝑓.
𝑟𝑟 is a solution to the equation 𝑓𝑓(𝑥𝑥) = 0.
𝑟𝑟 is a root of a polynomial function 𝑓𝑓.

Foundation Program/ Math Department Page 1 Spring 2021

Pre-Calculus _ Chapter 5

Example 1: Finding a Polynomial Function from its Zero.

Find a polynomial function of degree 3 whose zeros are −3, 2 𝑎𝑎𝑎𝑎𝑎𝑎 5 and the
point (3, −36) is a point on the graph of the function.

Note:
If (𝑥𝑥 − 𝑟𝑟)𝑚𝑚 is a factor of a polynomial 𝑓𝑓, and (𝑥𝑥 − 𝑟𝑟)𝑚𝑚+1 is not a factor of 𝑓𝑓 then 𝑟𝑟 is
called a zero of multiplicity 𝒎𝒎 of 𝒇𝒇.

Example 2: Identifying Zeros and Their Multiplicities.

Identify the zeros and their multiplicities for the polynomial
2
1 4
𝑓𝑓(𝑥𝑥) = 5(𝑥𝑥 − 2)(𝑥𝑥 + 3) �𝑥𝑥 − � .
2

Foundation Program/ Math Department Page 2 Spring 2021

 Pre-Calculus _ Chapter 5

Example 3: Identifying Zeros and Their Multiplicities.

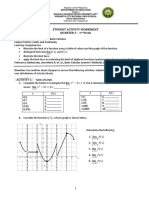
For the polynomial: 𝑓𝑓(𝑥𝑥) = 𝑥𝑥 2 (𝑥𝑥 − 2) .
a) Find the 𝑥𝑥 − 𝑎𝑎𝑎𝑎𝑎𝑎 𝑦𝑦 − 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖 of the graph of 𝑓𝑓(𝑥𝑥)

b) Use the 𝑥𝑥-intercepts to find the interval(s) on which the graph of 𝑓𝑓(𝑥𝑥) is above the 𝑥𝑥-axis
and the interval(s) on which the graph of 𝑓𝑓(𝑥𝑥) is below the 𝑥𝑥-axis.

c) Locate other points on the graph and connect all the points plotted with a smooth,
continuous curve.

𝑥𝑥
𝑦𝑦

Foundation Program/ Math Department Page 3 Spring 2021

Pre-Calculus _ Chapter 5

Remark:
Behavior of the graph near a zero
If 𝒓𝒓 is a Zero of even multiplicity

• The sign of 𝑓𝑓(𝑥𝑥) does not change from one side to other side of 𝑟𝑟.
• The graph of 𝑓𝑓 touches the 𝑥𝑥-axis at 𝑟𝑟.

If 𝒓𝒓 is a Zero of odd multiplicity

• The sign of 𝑓𝑓(𝑥𝑥) change from one side to the other side of 𝑟𝑟.
• The graph of 𝑓𝑓 crosses the 𝑥𝑥-axis at 𝑟𝑟.

Remark: Turning Points (The points at which a graph changes direction.)

If 𝑓𝑓 is a polynomial function of degree 𝒏𝒏, then the graph of 𝑓𝑓 has at most 𝒏𝒏 − 𝟏𝟏 turning
points.

If the graph of a polynomial function 𝑓𝑓 has 𝒏𝒏 − 𝟏𝟏 turning points, then the degree of 𝑓𝑓
is at least 𝒏𝒏 .

Example 4: Identifying the Graph of Polynomial Function.

What is the degree of the following functions?

b)
a)

Number of turning points: Number of turning points:

Number of 𝑥𝑥 − 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖: Number of 𝑥𝑥 − 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖:
Degree: Degree:

Foundation Program/ Math Department Page 4 Spring 2021

Pre-Calculus _ Chapter 5

c)

Number of turning points:

Number of 𝑥𝑥 − 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖:
Degree:

Example 10: Identifying the Graph of Polynomial Function.

Which of the graphs could be the graph of a polynomial function?

a)

b) c)

Foundation Program/ Math Department Page 5 Spring 2021

Pre-Calculus _ Chapter 5

The behavior of the graph of a function for large values of x, either positive or negative,
is referred to as its end behavior.

THEOREM

End Behavior
For large values of 𝑥𝑥, either positive or negative, the graph of the polynomial function

resembles the graph of the power function

Example 11: Identifying the Graph of Polynomial Function.

Which of the graphs could be the graph of (𝑥𝑥) = 𝑥𝑥 4 + 5𝑥𝑥 3 + 5𝑥𝑥 2 − 5𝑥𝑥 − 6 .

Foundation Program/ Math Department Page 6 Spring 2021

Pre-Calculus _ Chapter 5

2- Analyze the Graph of a Polynomial Function

Example 12: How to Analyze the Graph of a polynomial Function.

Analyze the graph of the polynomial function 𝑓𝑓(𝑥𝑥) = (2𝑥𝑥 + 1)(𝑥𝑥 − 3)2 .

Step1: Expand 𝑓𝑓(𝑥𝑥)

Step 2: Find 𝑥𝑥 − 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖 and 𝑦𝑦 − 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖

Step 3: Find zeros of the function and their multiplicity

Zero Multiplicity Touch or cross 𝒙𝒙 − 𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂

Step 4: How many turning points?

Step 5: What is the behavior of the graph of 𝑓𝑓 near each 𝑥𝑥 − 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖.

Step 6: Put all information together to obtain the graph of 𝑓𝑓.

Foundation Program/ Math Department Page 7 Spring 2021

Pre-Calculus _ Chapter 5

Example 13: How to Analyze the Graph of a polynomial Function.

Analyze the graph of the polynomial function 𝑓𝑓(𝑥𝑥) = 𝑥𝑥 2 (𝑥𝑥 − 4)(𝑥𝑥 + 1) .

Step1: Expand 𝑓𝑓(𝑥𝑥)

Step 2: Find 𝑥𝑥 − 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖 and 𝑦𝑦 − 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖

Step 3: Find zeros of the function and their multiplicity

Zero Multiplicity Touch or cross 𝒙𝒙 − 𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂

Step 4: How many turning points?

Step 5: What is the behavior of the graph of 𝑓𝑓 near each 𝑥𝑥 − 𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖𝑖.

Step 6: Put all information together to obtain the graph of 𝑓𝑓.

For more example: https://www.youtube.com/watch?v=q6vgQEZuNKk

Foundation Program/ Math Department Page 8 Spring 2021

Pre-Calculus _ Chapter 5

Extra Exercises for students

1) Identify which of the graphs could be the graph of a polynomial function. For those that could,
list the state the least degree the polynomial can have. For those that could not, say why not.
1) 2)

3) 4)

2) Construct a polynomial function that might have the given graph. (More than one answer may
be Possible.)
1)

Foundation Program/ Math Department Page 9 Spring 2021

Pre-Calculus _ Chapter 5

2)

3)

3) Analyze each polynomial function by following step1 through 6.

1) 𝑓𝑓(𝑥𝑥) = 𝑥𝑥 2 (𝑥𝑥 − 3) 2) 𝑓𝑓(𝑥𝑥) = −2(𝑥𝑥 + 2)(𝑥𝑥 − 2)3

3) 𝑓𝑓(𝑥𝑥) = 𝑥𝑥 2 (𝑥𝑥 − 2)(𝑥𝑥 + 2) 4) 𝑓𝑓(𝑥𝑥) = (𝑥𝑥 − 22 )(𝑥𝑥 + 2)(𝑥𝑥 + 4)

Foundation Program/ Math Department Page 10 Spring 2021