7-Geometric Meaning of Partial Derivative VU

Lecture No. 7

Geometric Meaning of Partial Derivative

Geometric meaning of partial derivative

z = f(x, y)

z f
Partial derivative of f with respect of x is denoted by or f x or .
x x

z f
Partial derivative of f with respect of y is denoted by or f y or .
y y

Partial Derivatives

Let z = f(x, y) be a function of two variables defined on a certain domain D.

For a given change ∆x in x, keeping y as constant, the change ∆z in z, is given by

z  f ( x  x, y )  f ( x, y )

z f ( x  x, y )  f ( x, y )
If the ratio  approaches to a finite limit as ∆x →0, then this limit is
x x
called Partial derivative of f with respect of x.

Similarly for a given change ∆y in y, keeping x as constant, the change ∆z in z, is given by

z  f ( x, y  y )  f ( x, y )

z f ( x , y  y )  f ( x , y )
If the ratio  approaches to a finite limit as ∆y →0, then this limit is
y y
called Partial derivative of f with respect of y.

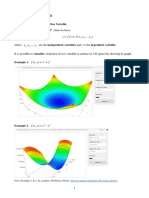
Geometric Meaning of Partial Derivatives

Suppose z = f(x, y) is a function of two variables. The graph of f is a surface. Let P be a point on
the graph with the coordinates ( x0 , y 0 , f ( x 0 , y 0 )) . If a point starting from P, changes its position
on the surface such that y is constant, then the locus of this point is the curve of intersection of
z
z = f(x, y) and y = constant. On this curve, is a derivative of z = f(x, y) with respect to x with
x
y constant.

© Copyright Virtual University of Pakistan

7-Geometric Meaning of Partial Derivative VU

z
Thus, = slope of the tangent to this curve at P.
x

z
Similarly, is the gradient of the tangent at P to this curve of intersection of z = f(x, y) and
y
x = constant.

As shown in the figure below (left). Also together these tangent lines are shown in figure below
(right).

© Copyright Virtual University of Pakistan

7-Geometric Meaning of Partial Derivative VU

Partial Derivatives of Higher Orders

The partial derivatives fx and fy of a function f of two variables x and y, being functions of x and
y, may possess derivatives. In such cases, the second order partial derivatives are defined as
below:

  f   2 f 
   f x    f x x  f xx f x2
x  x  x 2 x
  f   2 f 
   f x    f x y  f xy
y  x  yx y
  f   2 f 
    f y   f 
y x  f yx
x  y  xy x
  f   2 f 
   f   f   f f
y  y  y 2 y
y y y yy y2

Thus there are four second order partial derivatives for a function z = f(x, y). The partial
derivatives fxy and fyx are called Mixed Second partials and are not equal in general. Partial
derivatives of order more than two can be defined in a similar manner.

2z 2z x

Example 1: Find and for z  arc sin  
xy y x  y

x
Solution: z  arc sin  
 y

z    x  1  x y 1
  arc sin         
x 
x  
 y   x  x  y 
2
y2  x2  y
1   
 y
1

y  x2
2

z    x  1  x y  x
  arc sin        2 
y y  2 y  y 
 y  x   y2  x2  y 
1   
 y
x

y y2  x2

© Copyright Virtual University of Pakistan

7-Geometric Meaning of Partial Derivative VU

  z    x 

  
x  y  x  y y 2  x 2 
 
 
2z 1 x x 
 
 3

  y  x 2 
xy y y x 2 2 y 2 2

 y2  x2  x2
 3
y  y 2  x 2 2
y
 3
y 2  x 2 2
  z    1 

  
y  x  y  y 2  x 2 
 
2
 z 1 2 3
 2
yx

2
 y  x2  2


y
 y  x2 

1
 3
 2y
2 y  x 
2 2 2

y
 3
y 2
 x 2 2
2z 2z
Here, you can see that 
yx xy

Example 2

2 f 2 f 2 f 2 f
Find , , and for f ( x , y )  x cos y  y e x .
x 2 y 2 y x x y

Solution:

f 
 x cos y  y e x   cos y  y e x
x x
f 
 x cos y  y e x    x sin y  e x
y y
2 f   f  
   cos y  y e   0  y e  y e
x x x
2

x x  x  x
2 f   f  
    cos y  y e x    sin y  e x
yx y  x  y

© Copyright Virtual University of Pakistan

7-Geometric Meaning of Partial Derivative VU

2 f   f  
     x sin y  e x    sin y  e x
xy x  y  x
 2 f   f  
     x sin y  e x    x cos y
y 2 y  y  y

Laplace’s Equation

For a function w  f ( x, y, z ) , the equation

2 f 2 f 2 f
  0
x 2 y 2 z 2

is called Laplace’s equation.

Example 3: Show that the function f ( x, y )  e x sin y  e y cos x satisfies the Laplace’s equation.

Solution: f ( x, y )  e x sin y  e y cos x

f 
  e x sin y  e y cos x   e x sin y  e y sin x
x x
f 
 e x sin y  e y cos x   e x cos y  e y cos x
y y
2 f   f   x
   e sin y  e sin x   e sin y  e cos x
y x y
2

x x  x  x
2 f   f  
2
    e x cos y  e y cos x    e x sin y  e y cos x
y y  y  y

Adding both partial second order derivatives, we have

2 f 2 f
2
 2
 e x sin y  e y cos x    e x sin y  e y cos x 
x y
0

© Copyright Virtual University of Pakistan

7-Geometric Meaning of Partial Derivative VU

Euler’s Theorem

The Mixed Derivative Theorem

If f(x, y) and its partial derivatives f , f , f and f are defined throughout an open region
x y xy yx
containing a point (a, b) and are all continuous at (a, b), then

fxy(a , b) = fyx (a , b)

Advantage of Euler’s theorem

ey
w  xy 
y2 1

2w
The symbol tells us to differentiate first with respect to y and then with respect to x.
x y
However, if we postpone the differentiation with respect to y and differentiate first with respect
to x, we get the answer more quickly.

w   ey 
  xy  2   y  0  y
x x  y 1

 2 w   w  
and     y 1
yx y  x  y

Overview of lecture# 7

Chapter # 16 Partial derivatives

Page # 790 Article # 16.3

© Copyright Virtual University of Pakistan